


Naprej: Zunanja obremenitev
Gor: Splošen postopek MKE
Nazaj: Enačba konstrukcije
Vsebina: 
Pogoj stabilnosti konstrukcije zahteva da je del vosliščnih pomikov ali
zasukov poznan. Poznani vozliščni pomiki (zasuki, tangente, ..) predstavljajo
robne pogoje. Ker so pomiki in sile ter zasuku in momenti konjugirane veličine
, lahko z poznavanjem ene veličine izrazimo njen konjugirani par. To storimo s
parcioniranjem enačbe  . Enačbo parcioniramo tako, da v vektorju
pomikov konstrukcije
. Enačbo parcioniramo tako, da v vektorju
pomikov konstrukcije 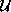 združimo vse poznane komponente v Podmatriko
združimo vse poznane komponente v Podmatriko
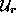 ostale nezane komponente pa v podmatriko
ostale nezane komponente pa v podmatriko 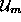 . Enako
parcioniramo vektor
. Enako
parcioniramo vektor 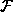 , kjer so v podmatriki
, kjer so v podmatriki 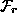 zbrane vse
komponente rezcij, v matriki
zbrane vse
komponente rezcij, v matriki 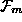 pa poznane obremenitve. Tako dobimo
parcionirano enačbo kostrukcije
pa poznane obremenitve. Tako dobimo
parcionirano enačbo kostrukcije
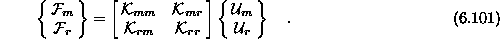
Po množenju dobimo
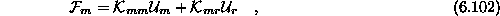
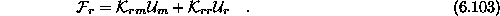
Ponavadi so vse kompomente vektorja 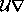 poznane, so enake nič, ker
imamo nepodajne podpore. Tako iz enačbe
poznane, so enake nič, ker
imamo nepodajne podpore. Tako iz enačbe  izrazimo
izrazimo
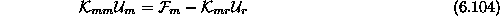
ali
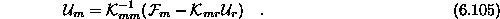
Če v zadnji enabi upoštevamo da je v večini primerov 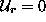 sledi
sledi

Z vsemi znanimi pomiki je problem statično rešen. Z upoštevanjem zvez med
pomiki in deformacijami ter pomiki in napetostmi izračunamo slednje.
Leon Kos
Mon Apr 22 10:36:01 GMT+0100 1996
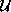 združimo vse poznane komponente v Podmatriko
združimo vse poznane komponente v Podmatriko
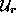 ostale nezane komponente pa v podmatriko
ostale nezane komponente pa v podmatriko 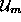 . Enako
parcioniramo vektor
. Enako
parcioniramo vektor 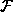 , kjer so v podmatriki
, kjer so v podmatriki 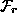 zbrane vse
komponente rezcij, v matriki
zbrane vse
komponente rezcij, v matriki 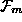 pa poznane obremenitve. Tako dobimo
parcionirano enačbo kostrukcije
pa poznane obremenitve. Tako dobimo
parcionirano enačbo kostrukcije
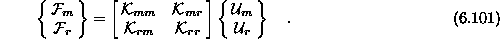
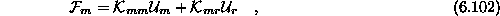
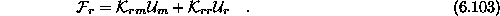
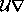 poznane, so enake nič, ker
imamo nepodajne podpore. Tako iz enačbe
poznane, so enake nič, ker
imamo nepodajne podpore. Tako iz enačbe 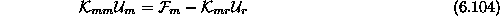
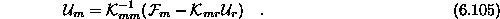
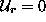 sledi
sledi
