Diskretizirana konstrukcija ima e elementov in n vozlišč. Z združitvijo vseh enačb končnih elemtov dobimo enačbo konstrukcije, ki jo zapišemov simbolični obliki
Vektorja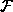 
in 
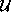sta
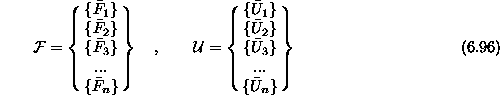
Vsaka podmatrika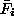 
in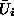 
je podana v globalnem koordinatnem
sistemu in ima toliko komponent kolikor prostostnih stopenj ima vsako
vozlišče.
Togostna matrika je sestavljena iz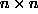 
podmatrik
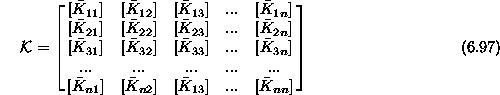
Podmatrike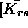 
dobimo tako, da togostne matrike posameznih
elementnov parcioniramo na podmatrike, ki pripadajo posamenznim vozliščem. Za
ploskoven trikotni končni element, vozlišči i, j in k bi bila enačba
konstrukcije po parcioniranju
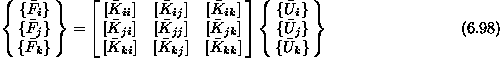
Dobljene podmatrike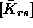 
, ki so podane v globalnem koordinatnem
sistemu, diagonalne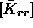 
ali pa izvendiagonalne
.
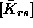Dagonalne podamtrike pripadajo vsakemu vozlišču n, sestavljene so iz toliko diagonalnih podmatrik kolikor elementov se stika v danem vozlišču, tako je
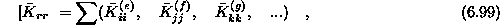
če se v vozlišču stika r elemetov. Da odpravimo potrebo za
označevanjeu notranjih točk elementa e velja dogovor, da označimo
vzamemo za točko i najmanjšo številčno oznako, ostale notranje točke
pa ji slede v protiurini smeri obhoda. Izvendiagonalne podmatrike
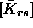se pojavljajo, če je vozlišče s sosednje vozlišču
r, ki ga obravnavamo. Podmatrika je sestavljena iz dveh podamtrik, kadar
se elementa stikata na zveznici rs
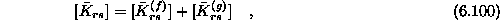
ali eno samo podmatriko če zveznici rs pripada en sam element (naprimer element na konturi). Označevanje vozlišč končnih elementov je poljubno, priporočljivo pa je, da je način označevanja tak, da dobimo čim ožjo pasovno matriko.
