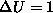Pri primerih izracuna prostornine, ki jo obdaja ploskev smo videli, da je
mozno tocno izracunati interpolirano prostornino, ze ce smo
poznali vrednosti funkcije U v vozliscih. Problem pri MKD je prav
ta, da je potrebno funkcijo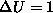 
zadostiti z diskretizacijo,
ki se napenja preko vecih tock in povezuje posamezne osnovne
elemente (ploskvice).
Pri metodi MKE so kot osnovne neznanke vrednosti
napetostne funkcije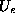 
v vozliscih. Zveza med 
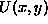v
elementu in vrednostmi funkcije v vozliscih pa se vzpostavlja z
interpolacijskimi funkcijami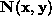 
.
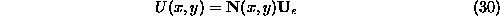
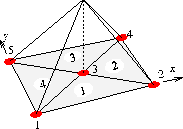
Za osnovo in zgled MKE izberimo pravokotnik dimenzije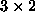 
na
sliki 7 in najenostavnejsi dvodimenzionalni trikotni
element CST ( Constant Strain Triangle) za katerega so
interpolacijske funkcije
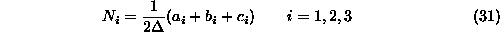
Kjer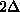 
predstavlja dvakratno povrsino trikotnika
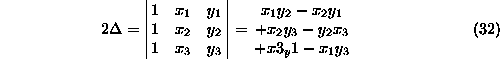
izrazi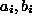 
in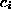 
pa so za prvi element enaki
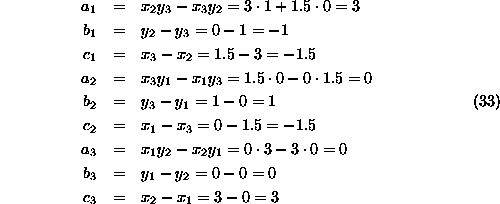
Enacbo elementa CST lahko zapisemo kot
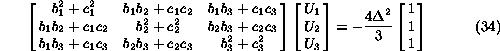
Za prvi element je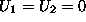 
in enacba elementa
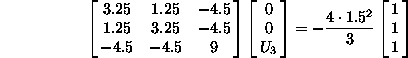
Podobno je za drugi element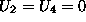 
in enacba elementa
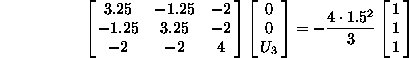
Za stiri koncne elemente smo dobili stiri enacbe za vrednost
funkcije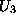 
, kar pomeni, da je sistem predolocen. Ce bi bili vsi
elementi enake oblike, bi bile enacbe za tocko 3 enake in bi
uporaba ene enacbe zadovoljila tudi ostale tri. Zal v nasem primeru
to ni tako, zato se odlocimo za izracun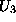 
tako, da bo
izracunana vrednost 
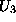v povprecju zadovoljila vse enacbe. To
naredimo tako, da vse enacbe za tocko 3 sestejemo in resimo. S tem
dobimo povprecno vrednost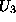 
. Iz navedenega lahko sklepamo, da
lahko po izracunu vrednosti v tockah enostavno ocenimo napako v
vozliscih in primerno ukrepamo z zgostitvijo mreze na kriticnih
mestih. Glavna slabost elementov CST je obcutljivost na
deformacije. Priljubljeni pa so zaradi enostavnosti in
prilagodljivosti na modelirano obliko.
Ob upostevanju enacb vseh stirih elementov dobimo skupno enacbo za tocko 3, ki je edina neznanka sistema
Za izracun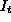 
je potrebno izracunati prostornino vseh tristranih
prizem, ki sestavljajo mrezo koncnih elementov. Prostornina poljubno
prisekane tristrane prizme z vrednostmi v ogljiscih a, b in c in
povrsino osnovne ploskve 
se izracuna kot
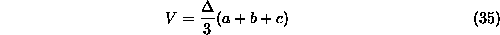
Torzijski moment za primer na sliki 7 je tako
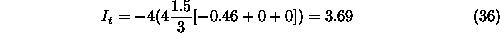
kar je v primerjavi z metodo MKD, kjer smo za isti prerez uporabili dve notranji tocki, veliko bolje vendar se vedno ne dovolj natancno. Daje pa razultat slutiti, da metoda MKE veliko hitreje konvergira k tocni resitvi.