Poljska in interpolacijska matrika končnega elementa

Konstrukcijo razdelina na končen elemente - jo diskretiziramo. Vsak elemet ima polje ter vozlišča.

 

Prek vozlišč je konstrukcija povezana v celoto. Zanima nas pomik v polju končnega elementa, ki je funkcija koordinat za splošno oblikovano in obremenjeno konstrukcijo. V večini primerov funkcije koordinat pomikov vnaprej niso znane

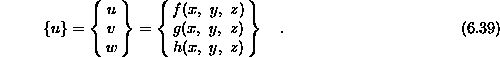
ali v matričnem zapisu

V tej enačbi je 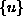vektor pomika v polju končnega elementa. Matrika je poljska matrika elementa, vektor 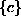pa vektor konstant. Komponente vektorja konstant morajo biti izbrane tako, da zavzame vektor pomikov 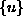v vozliščih predpisane vrednosti. Poljska matrika razen za linijske elemente ni poznana in jo je potrebno izbrati za vsak končni element posebej.

Izbiro poljske matrike ilustrira naslednji primer, ko izberemo poljsko matriko za trikotni končni element stene. Za dovolj majhen končni element lahko predpostavimo linearno spremembo pomikov v polju elementa. Ob upoštevanju, da je stena dvodimenzionalen konstrukcijski element, zapišemo vektor pomikov

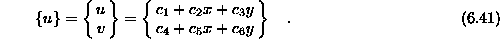
Če naredimo dekompozicijo zgornjega vektorja dobimo poljsko matriko in vektor konstant

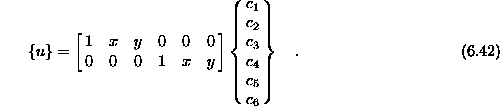
Poljska matrika je tako

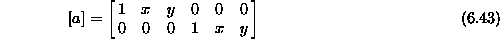
in vektor konstant

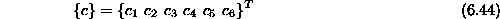
Linearna predpostavka o pomikih v poljiu je zelo groba zato je potrebno uporabiti večje število končnih elementov. S parabolično predpostavko o pomikih v polju pa bi bila poljska matrika

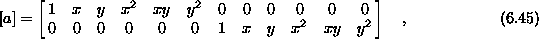
vektor pomikov pa bi imel 12 konstant. Z višjimi polinomi dobimo natančnejše poteke pomikov v poljih, kar pa zahteva večje število računskih operacij. Izbira matrike in vektorja 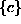ni čisto poljubna in je odvisna od pogoja izpolnitve robnih pogojev. Definirajmo vozliščni vektor, ki ga sestavljajo vektorji pomikov v posamenznih vozliščih. V primeru dvodimenzionalnega trikotnega elementa ima ta vsega skupaj tri vozlišča v katerem so možni pomiki v x in y smeri. Iz tega sledi da ima vozliščni vektor 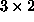komponent

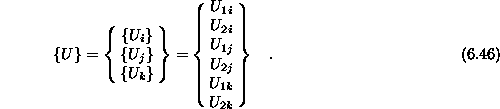
Sledi da lahko za vozliščni vektor s 6 komponentami zapišemo samo šest robnih pogojev tako da ima vektor konstant 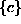lahko samo 6 komponent. To omejitev lahko odpravimo s tem da v vozliščnem vektorju poleg pomikov predpišemo tudi odvode v smeri pomikov. Vozliščni vektor bi tako imel v posameznem vozlišču 6 komponent

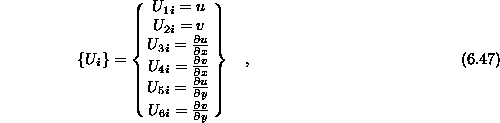
vsega skupaj 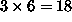komponent. Številu komponent vozliščnega vektorja pravimo tudi število prostostnih stopenj. Od izbranega vozliščnega vektorja sta odvisna vektor konstant in poljska matrika, saj mora vektor konstant imeti toliko komponent kolikor jih ima vozliščni vektor.

Ker morajo v vozliščih veljati robni pogoji pišemo za robne pogoje

in enačba je tako

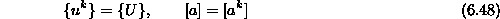
kjer je z indeksom k povdarjeno, da gre za izpolnitev robnih pogojev. Matriko 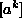imenujemo poljska matrika robnih vrednosti in je konstantna. Je kvadratna matrika in nesingularna zato jo je možno invertirati. Enačbo zapišemop še v obliki

ali

Če enačbo vstavimo v enačbo dobimo

Uvedemo še eno poenostavitev

in je

Zadnja enačba podaja zvezo med vektorjem pomikov v polju elementa 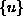in vozliščnim vektorjem 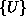. Matriko 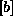pa imenujemo interpolacijska matrika (oblikovna, shape function). Z izbiro interpolacijske matrike potekajo nadaljni izračunu MKE po enotnem postopku. Končne elementi, ki ustrezajo prej opisanim pogojem imenujemo kompatibilne končne elemente (izoparametrični končni elementi). Poznamo pa tudi komčne elemente pri katerih imamo več ali manj vozliščnih parametrov (super ali subparametrični elementi).