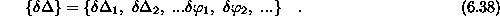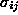 , deformacijskega tenzorja
, deformacijskega tenzorja 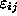 in vektorja
pomikov
in vektorja
pomikov 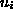 .
Tenzor napetosti
.
Tenzor napetosti
Metoda končnih elementov temelji na enačba elasto mehanike saj z njihovo
pomočjo definiramo povezavo med pomiki v polju in vozliščih elementa.
Probleme elastomehanike opišemo z elementi napetostnega tenzorja
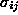 , deformacijskega tenzorja
, deformacijskega tenzorja 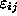 in vektorja
pomikov
in vektorja
pomikov 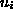 .
Tenzor napetosti
.
Tenzor napetosti
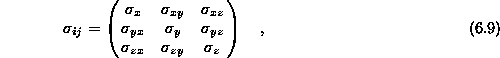
tenzor specifičnih deformacij
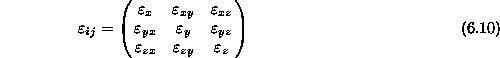
in vektor pomikov

=1000
V zgornjih treh enačbah natopa 15 neznank. Rabimo torej 15 enačb
za rešitev elastomehanskega problema. Komponente obeh tenzorjev
in vektorja med seboj povezujejo enačbe elastomehanike.
a.) Ravnotežne enačbe statike
=10000
eksplicitno v kartezijevih koordinatah
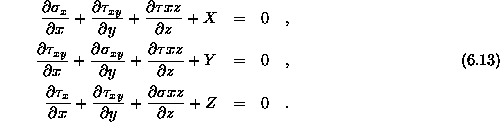
b.) Zveza med malimi specifičnimi deformacijami in pomiki
ali v eksplicitni obliki
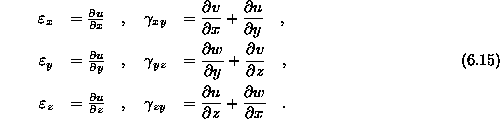
c.) Povezava napetosti in deformacij Za Hookov material in majhne deformacije je ta zveza
ali v komponentni obliki
V enačbi je volumska diletacija

Koeficienta 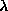 in
in 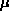 pa sta Laméjevi konstanti
pa sta Laméjevi konstanti
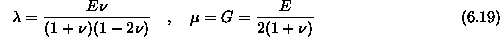
in  Poissonovo število.
V enačbah
Poissonovo število.
V enačbah ![]() in
in ![]() so napetosti izražene
s specifičnimi deformacijami. Namesto teh enačb lahko uporabimo tudi
enačbe v katerih nastopajo specifične deformacije izražene z napetostmi.
Za ta primer je enačba
so napetosti izražene
s specifičnimi deformacijami. Namesto teh enačb lahko uporabimo tudi
enačbe v katerih nastopajo specifične deformacije izražene z napetostmi.
Za ta primer je enačba
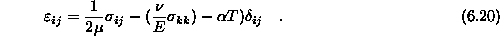
Opisane enačbe upoštevajo tudi napetosti in deformacije, ki izvirajo iz tempraturne obremenitve T. V primeru, da porazdelitev v kontinuumu vnaprej ni poznana uporabimo prenosno enačbo za prenos toplote

Tudi to enačbo rešimo z MKE. Če enače opisane v točkah (a), () in (c) zapišemo v komponentni obliki dobimo 15 enačb, ki omogočijo rešitev sistema s petnajstimi neznankami. Pri reševanju pa moramo upo"tevati še robne pogoje in zunanje obremenitve.
V primeru robnih pogoje so na povšini določene sile

ali pa pomiki

Velikokrat pa se na konstrukcijah pojavljajo mešani robni pogoji pri čemer so na delu konstrukcije določene sile drugod pa pomiki.
Sistem enačb elastomehanike da enoli"no rešitev le v primeru da so izpoljene kompatibilnostne enačbe
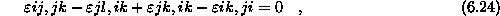
ki so zadosten pogoj za enolično rešitev le za enkrat povezana območja. V primeru večkrat povezanih območij moramo uporabiti dodatne enačbe, ki zagotavljajo enoličnost pomikov okoli notranjih zaključenih ploskev. Namesto ravnotežnih enačb, pri MKE, uporabljamo princip virtualnih pomikov, ki pravi, da je za ravnotežne sisteme virtualno delo zunanjih sil enako virtualnemu delu notranjih sil

V eksplicitni obliki pa
Enačbe elasto mehani zapišemo v matrični obliki, ki je mnogo bolj primerna za programiranje. Tenzorja napetosti in deformacij ter vektor pomikov so v matričnem zapisu posplošeni vektorji
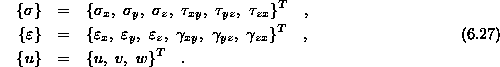
Sedaj lahko zapišemo ravnotežno enačbo ![]() v matrični obliki
v matrični obliki
V tej enačbi je matrika diferencialnih operatorjev

Vektor volumskih sil pa je
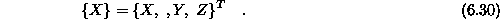
Enačbo ![]() zapišemo v eksplicitni obliki
zapišemo v eksplicitni obliki
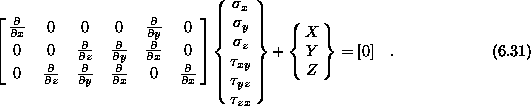
Prav tako tudi enačbo specifičnih deformacij ![]() zapišemo v
matrični obliki
zapišemo v
matrični obliki

ali v komponentni obliki
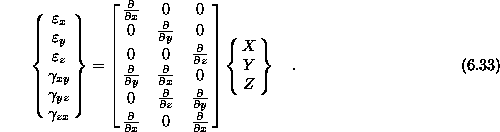
Hookov zakon podan z enačbo ![]() zapišemo v matrični obliki
zapišemo v matrični obliki

ali v komponentni obliki
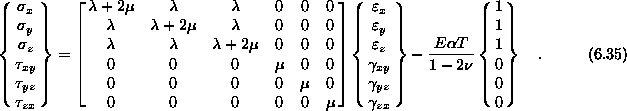
Matriko E imenujemo matrika elastičnih konstant, vektor 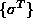 pa temperaturni vektor.
Princip virtualnih pomikov
pa temperaturni vektor.
Princip virtualnih pomikov ![]() je v matrične zapisu
je v matrične zapisu
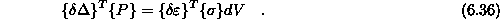
V enačbi je 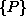 generalizirani vektor, ki zajame sile in momente
generalizirani vektor, ki zajame sile in momente
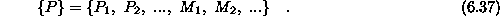
Tem silam pa ustrezajo virtualni pomiki in zasuki