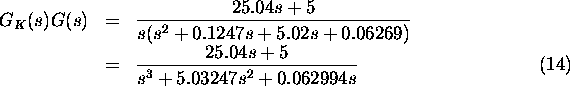S pomo"cjo diagrama lege korenov dolo"cimo lego dominantnih polov zaprtozan"cnega sistema.

Ker ke kot sistema v to"cki 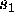
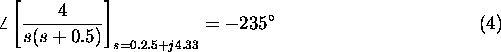
Izra"cunamo kot 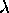 , ki ga mora vnesti prehitevalni kompenzator,
da poteka DLK skozi "zelena pola. Pri tem predpostavimo, da bomo
kasneje izbrali
, ki ga mora vnesti prehitevalni kompenzator,
da poteka DLK skozi "zelena pola. Pri tem predpostavimo, da bomo
kasneje izbrali  zadosti velik, da bo prispevek zakasnilnega
kompenzatorja po absolutni vrednosti in kotu majhen v "zeljenih polih.
Prispevek prehitevalnega kompenzatorja mora torej biti
zadosti velik, da bo prispevek zakasnilnega
kompenzatorja po absolutni vrednosti in kotu majhen v "zeljenih polih.
Prispevek prehitevalnega kompenzatorja mora torej biti
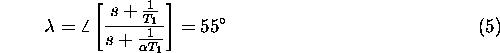
Ni"clo prehitevalnega kompenzatorja izberemo tako, da kraj"sa pol
sistema pri 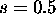 . Grafi"cno dolo"cimo "se lego pola
prehitevalnega kompenzatorja:
ni"cla je pri
. Grafi"cno dolo"cimo "se lego pola
prehitevalnega kompenzatorja:
ni"cla je pri 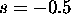 in pol pri
in pol pri 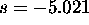
Prehitevalni kompenzator ima tako prenosno funkcijo

in sta ustrezni konstanti

Iz pogoja absolutne vrednosti nato dolo"cimo konstanto 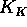
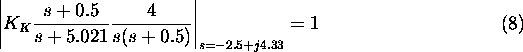
oz.
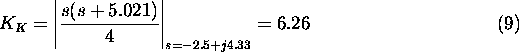
S tem smo dolo"cili prehitevalni kompenzator. Konstanto 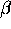 zakasnilnega kompenzatorja kolo"cimo iz pogoja za konstanto
hitrostnega pogre"ska.
zakasnilnega kompenzatorja kolo"cimo iz pogoja za konstanto
hitrostnega pogre"ska.
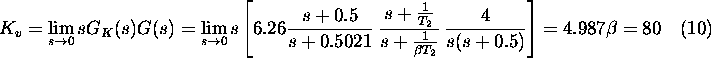
Torej je 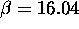
Kon"cno izberemo 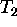 , tako da bo izpolnjeno
, tako da bo izpolnjeno
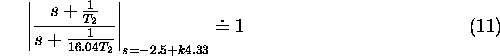
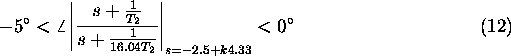
Prvi pogoj zahteva "cim ve"cji 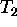 , drugi pogoj pa zadovoljimo s
, drugi pogoj pa zadovoljimo s
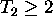 .
.
Izberimo 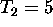 oz. ni"clo zakasnilnega kompenzatorja
pri
oz. ni"clo zakasnilnega kompenzatorja
pri 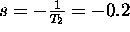 in pol pri
in pol pri 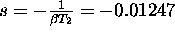
Na"crtani kompenzator podaja prenosna funkcija
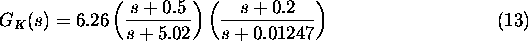
Prenosna funkcija kompenziranega sistema je tako