Univerza v Ljubljani

Fakulteta za strojnistvo

Laboratorij za CAD - LECAD

Krivulje in povrsine v CAD

Predavanje

Tomaz Kolsek

Ljubljana, november 1997

Kazalo vsebine :

1 Uvod

2 Kubicne parametricne krivulje

3 Bezier-jeve krivulje

4 B-spline krivulje

5 Povecanje kontrole krivulj: NURBS

6 Parametricni popis povrsin

7 Literatura




1 Uvod



V nacrtovanju novih oblik je vedno igrala veliko vlogo interpolacija. Gre za problem, kako skozi mnozico podanih tock speljati gladko krivuljo. Veliko let so si obrtniki in nacrtovalci pomagali z tenkimi lesenimi oziroma kovinskimi trakovi ("spline"), ki so jih napeli na oporne tocke, po potrebi pa so jih se dodatno obtezevali s svincenimi utezmi. Obliko takega lesenega oziroma kovinskega traku poskusamo matematicno popisati z diferencialno enacbo

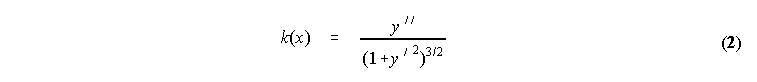Produkt E I predstavlja nek koeficient togosti in je konstanten, ce je trak konstantnega prereza. Ker ni drugih zunanjih sil med opornimi tockami in utezmi, je moment M(x) linearno odvisen od razdalje x. Oblika krivulje y=y(x) ima ukrivljenost
V primeru, da gre za majhne deformacije (y' << 1), je clen y' zanemarljiv, tedaj pa smemo enacbo (1) aproksimirati z EIy" = M(x), oziroma y(4) = 0. Oblika y=y(x) je tedaj odsekoma kubicna, je zvezna, ima pa zvezna tudi prvi in drugi odvod. Taksno je torej mehanicno ozadje krivulj, ki so se dolgo casa uporabljale za nacrtovanje in oblikovanje novih izdelkov.

Od krivulj, ki se uporabljajo v racunalniskih geometrijskih modelirnikih, se pricakujejo naslednje lastnosti:

- zveznost 0, 1. in 2. reda

- dobra preoblikovalnost, moznost lokalne in globalne kontrole

- ohranjevanje oblike pri geometrijskih transformacijah (rotacije v prostoru)

- teznja po zmanjsevanju variacije

- cim bolj enostaven matematicen popis

- univerzalnost matematicnega popisa za vse vrste standardnih oblik (ravne crte, deli kroznic, parabol, elips, polinomov, ..., pri povrsinah pa ravne ploskve, cilindricne povrsine, krogelne in interpolacijske)

Uveljavila sta se dva popisa in sicer Bezierjeve krivulje (povrsine) in NURBS (Non Uniform Rational B-Spline). Pierre Bezier je bil inzenir Renaulta, ki se je v 60. letih ukvarjal s problemom, kako prototipno geometrijo avtomobilske karoserije (katero so oblikovali iz npr. lesa) prenesti na risalne deske, oziroma jo nedvoumno matematicno dolociti. Leta 1966 je v reviji Automatisme objavil clanek, kjer je definiral 3D parametricen kubicen popis krivulj. P. Casteljau - inzenir Citroena, je razdelal tak popis ze prej, vendar je bil objavljen le v internem porocilu podjetja, tako da nosi matematicen popis Bezierjevo ime.



2 Kubicne parametricne krivulje



Zaradi zahtev po prostorskih transformacijah ne pridejo v postev funkcije v implicitni obliki f(x,y,z)=0 (oziroma dvodimenzionalne y=y(x)), zato se uporabljajo parametricne krivulje x=x(t), y=y(t) in z=z(t). Kot najbolj enostavne krivulje, ki so neproblematicno zvezne, so uporabljeni polinomi. Ce zahtevamo zveznost najmanj 2. reda, so torej ustrezne krivulje ze parametricni kubicni polinomi:

Parameter t lahko v splosnem tece v poljubnem intervalu, navajeni pa smo, da je normiran in se nahaja v intervalu [0,1]. Krivuljo lahko zapisemo v matricni obliki takole:
Ce koeficiente {ax, ay, az} zdruzimo v A, {bx, bx, bz} v B in tako naprej, lahko zapisemo:


3 Bezier-jeve krivulje

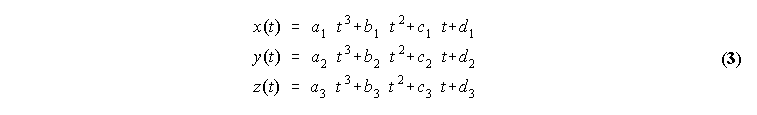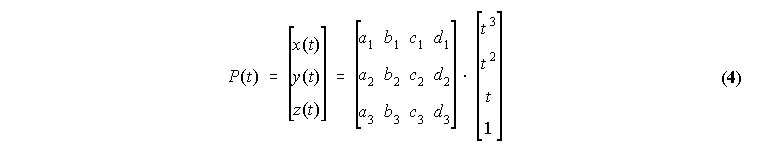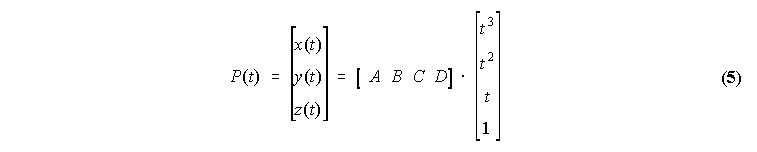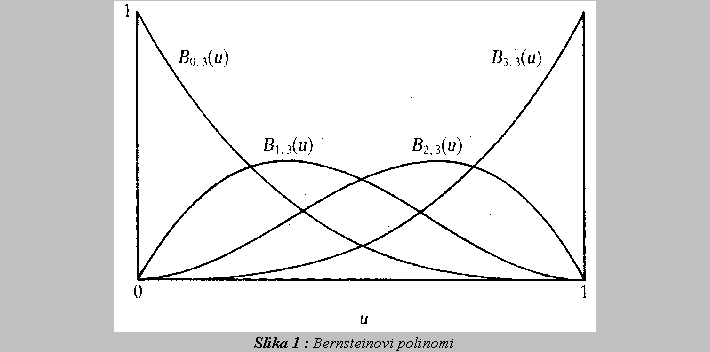
Med vsemi parametricnimi kubicnimi polinomi pa dobimo posebno imenitne, ce namesto enostavnih funkcij (t3,t2,t,1) (imenujemo jih tudi bazne funkcije) vzamemo t.i. Bernsteinove polinome (1-t)3, 3t(1-t)2, 3t2(1-t), t3. Tedaj lahko enacbo (5) zapisemo z drugacnimi koeficienti takole:

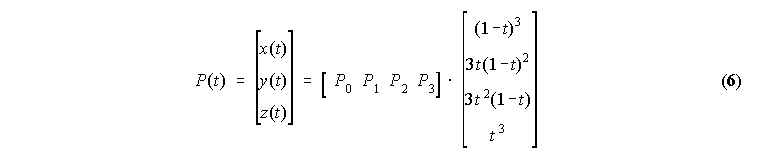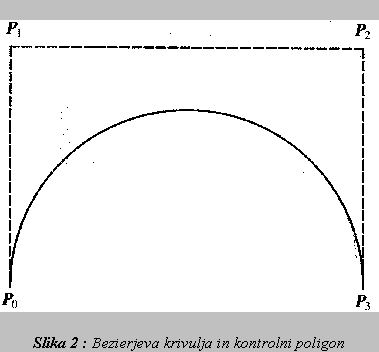
Enacba (6) predstavlja definicijo Bezierjevega kubicnega parametricnega polinoma in je genialna reformulacija hermitske oblike kubicnega polinoma. Izkaze se namrec, da lahko interpretiramo vektorje P0,P1,P2 in P3 kot {x,y,z} koordinate stirih tock, ki jih poimenujemo kontrolne tocke, povezavo P0-P1-P2-P3 pa kontrolni poligon (crtovje) parametricne kubicne krivulje P(t). Taksna interpretacija omogoca intuitivno dolocitev oblike krivulje v celoti le iz poznavanja polozaja stirih kontrolnih tock. Tako definirana krivulja je v naslednji povezavi s kontrolnimi tockami:

- krivulja se zacne v tocki P0 in konca v tocki P3

- krivulja je v tocki P0 oziroma P(t=0) tangentna na kontrolni poligon oziroma daljico P0P1, analogno je krivulja v tocki P3 oziroma P(t=1) tangentna na daljico P2P3

- krivulja se tockama P2 in P3 samo pribliza.

Bezierjeva krivulja ima se naslednje ugodne lastnosti:

- ravninski konveksni kontrolni poligon ima za posledico konveksno Bezierjevo krivuljo

- uporaba Bernsteinovih polinomov rezultira v lastnosti zmanjsevanja variacije

- obstaja tudi nacin, da rekonstruiramo obliko krivulje s posebnim geometrijskim nacrtovanjem le iz oblike kontrolnega poligona

Popis krivulj s kontrolnimi tockami ima npr. ugodno lastnost, da je pri geometrijskih transformacijah potrebno transformirati le kontrolne tocke, pa je ze mogoce dolociti krivuljo v transformiranem polozaju.

V matricni obliki, ki bi s koeficienti popisala tip povezovalne (bazne) funkcije, bi se za izbrane Bernsteinove polinome zgornja enacba glasila:

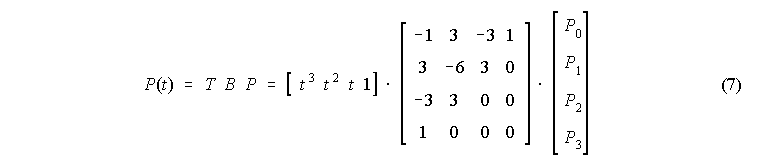Oblika (7) morda ni najprimernejsa za pomnjenje, pac pa je primerna za uporabo v racunalnikih.

Nabor stirih Bernsteinovih povezovalnih funkcij je poseben primer nabora povezovalnih funkcij reda n, ki se da zapisati takole:


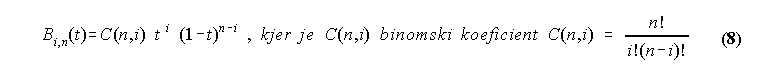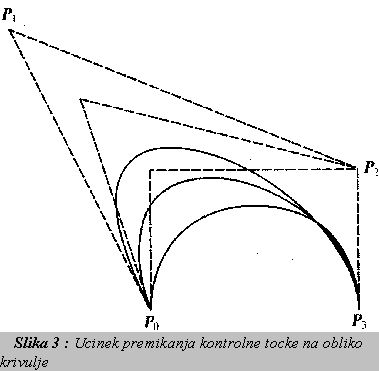
Uporaba Bezierjevih krivulj, ki so dolocene s pomocjo polinomov visjih redov v splosnem poveca stevilo kontrolnih tock, taka definicija pa bi povzrocila dodatne tezave pri racunalniski uporabi.


4 B-spline krivulje

Dve pomanjkljivosti Bezierjevih krivulj, namrec ne-lokalnost in povezava med stevilom kontrolnih tock in redom uporabljenega polinoma, je mogoce preseci z definiranjem B-spline krivulje. Prva pomanjkljivost - ne-lokalnost- povzroci, da ce premaknemo eno kontrolno tocko, se to do neke mere pozna na celotni krivulji. Druga pomanjkljivost pa je v tem, da Bezierjeve krivulje ne moremo nacrtati v splosnem skozi n tock, ne da bi "zlepili" vec razlicnih odsekov, ki so vsak zase posebej popisani.

Enako kot Bezierjeva krivulja je tudi B-spline dolocena s kontrolnim poligonom in se kontrolnim tockam le pribliza, le da je tock poljubno mnogo. B-spline je odsekoma kubicna na nekem intervalu parametra t, ko pa gre parameter t cez mejo intervala, se koeficienti spremenijo. Na dolocenem intervalu lahko primerjamo zapis B-spline z Bezierjevo krivuljo:


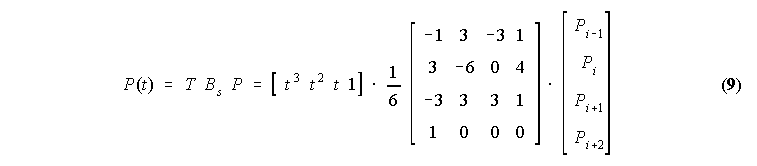Pi-1 .. Pi+2 so sedaj nabori stirih kontrolnih tock v mnozici vseh kontrolnih tock.

Krivuljo P(t) lahko izrazimo z povezovalnimi funkcijami takole:

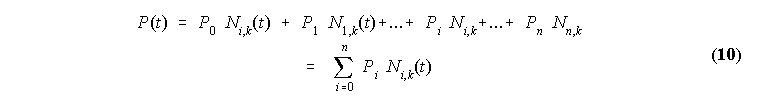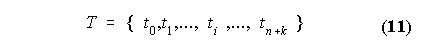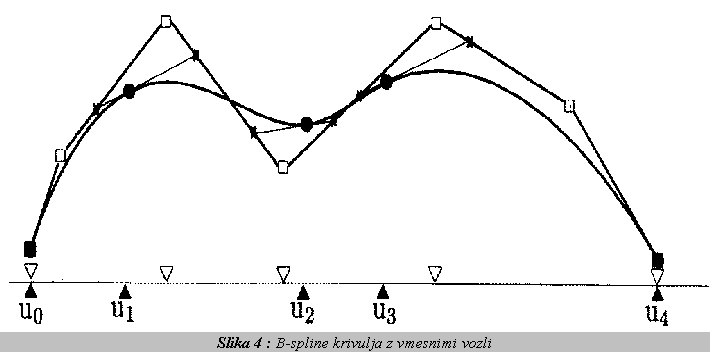V enacbi (10) torej nastopa krivulja, ki ima (n+1) kontrolnih tock, povezovalne funkcije pa so reda (k-1). Sedaj torej predstavljamo krivuljo kot mnozico polinomskih segmentov, vrednosti parametra t, kjer so segmenti zdruzeni, imenujemo vozlisca ti, mnozico vozlisc pa vozliscni vektor.

Uporabili pa nismo Bezierjevih (Bernsteinovih) povezovalnih funkcij, temvec nekoliko drugacno bazo. Bistvena razlika je v tem, da lahko pri B-spline povezovalnih funkcijah povecamo stevilo kontrolnih tock, ne da bi povisali red povezovalne funkcije. Povezovalne funkcije za B-spline lahko dolocimo s pomocjo rekurzivnega algoritma, ki ga je objavil C. d e Boor leta 1972:

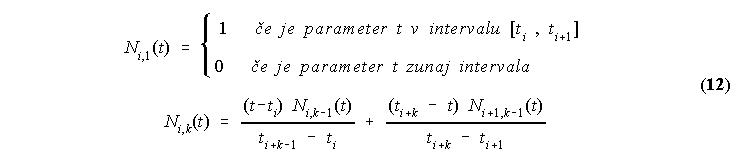Nekateri vozli se lahko veckrat ponovijo. Takim vozlom recemo periodicni oziroma uniformni. Vektor vozlov imenujemo neperiodicen oziroma neuniformen, kadar se samo prvih k in zadnjih k vozlisc ponovi, npr.

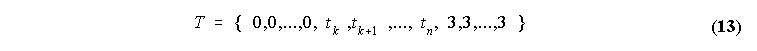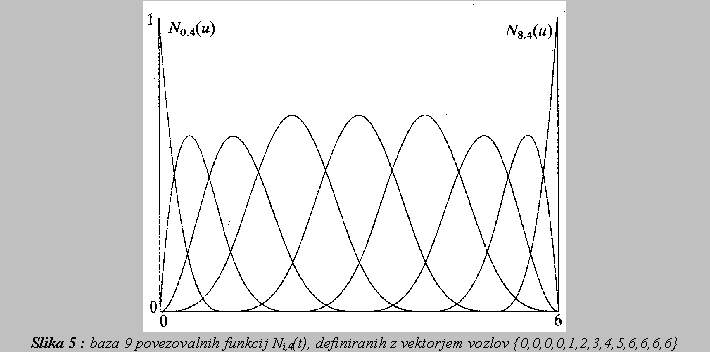
Ne-uniformne (Non-Uniform) B-spline krivulje so pravzaprav poseben primer, vendar se ravno ta popis najvec uporablja v racunalniskih geometrijskih modelirnikih. Razlog za popularnost je v tem, da se krivulja zacne in konca v zacetni in koncni kontrolni tocki ter da je krivulja v teh dveh tockah tangentna na kontrolni poligon (analogno kot pri Bezierjevi krivulji). Ce se uporabijo drugacne B-spline krivulje, konca krivulje ne sovpadeta z zacetno in koncno kontrolno tocko. Kadar se vozlisca ponavljajo, nastane v de-Boor algoritmu kvocient 0/0, kar pa se v aplikaciji izenaci z 0.

Primer:

Imejmo kontrolni poligon, kjer je podanih (n+1)=9 kontrolnih tock. Naj bodo povezovalne funkcije najvec tretjega reda, torej k=4. Torej nastopa 9 povezovalnih funkcij N0,4, N1,4, ..., N8,4, stevilo odsekov je 6, stevilo vozlov pa je n+k=13. Ne-uniformni vektor vozlov se torej glasi:

T = {0,0,0,0,1,2,3,4,5,6,6,6,6}.

Koncno, vektor vozlov

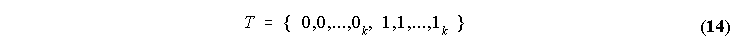definira Bezier-Bernstein-ovo povezovalno funkcijo reda (k-1). Torej lahko recemo, da je Bezierjeva krivulja poseben primer B-spline krivulje, ki je definirana z vozliscnim vektorjem, ki ne vsebuje notranjih vozlov.



5 Povecanje kontrole krivulj: NURBS



V primeru NURBS krivulj je kontrolni tocki B-spline krivulje dodana 4. koordinata, dodatni parameter, ki ga imenujemo utez in omogoca bolj prefinjeno lokalno kontrolo, kot je premikanje kontrolne tocke. Tako "obogateno" tocko bi takole zapisali:

Tridimenzionalno projekcijo krivulje, ki je definirana s takimi tockami, imenujemo racionalna B-spline krivulja in jo takole definiramo:
Izkaze se, da parameter w vpliva na krivuljo le lokalno: ce spremenimo utez na kontrolni tocki Pi, se bo to poznalo le na k odsekih. Geometricno lahko interpretiramo parameter w tudi kot magnet: Ce w narasca, se krivulja priblizuje kontrolni tocki in obratno. Navadne, ne-racionalne B-spline krivulje dobimo, ce so utezi enake 1 za vse kontrolne tocke.


6 Parametricni popis povrsin



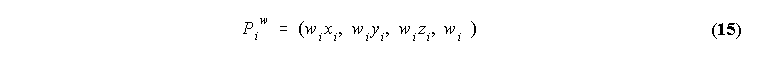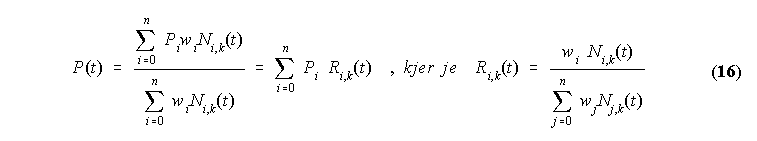Obravnava krivulj iz prejsnjih poglavij lahko enostavno posplosimo v dve dimenziji: tocka na povrsini je podana z bi-parametricno funkcijo, ki je sestavljena iz povezovalnih funkcij za vsak parameter posebej. Kubicna bezierjeva povrsina je torej takole definirana:

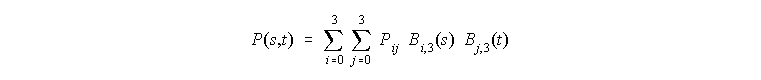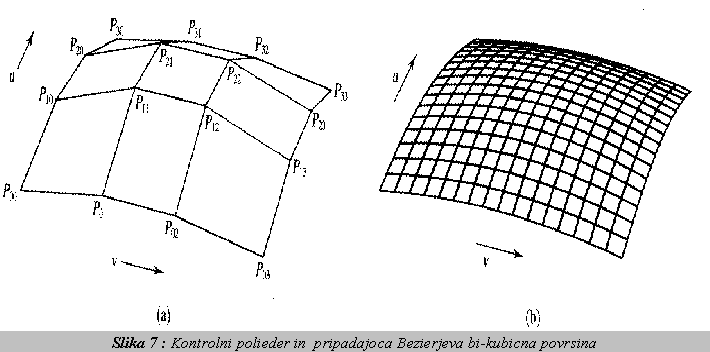Pij so sedaj kontrolne tocke, ki tvorijo polieder . 12 izmed kontrolnih tock lezi na robovih povrsine, 4 notranje tocke pa definirajo notranjo obliko povrsine. V matricni obliki bi tako povrsino zapisali:

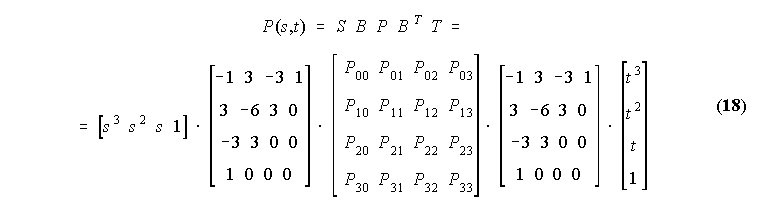Na analogen nacin bi definirali tudi B-spline povrsine:

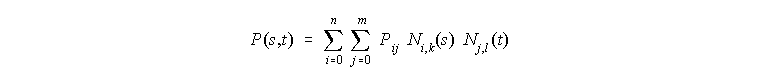Naenostavneje si predstavljamo taksen tip B-spline povrsine, kjer so vsi vektorji vozlov vseh povezovalnih funkcij ne-uniformni, torej se zacetni in koncni vozli ponovijo k-krat oziroma l-krat. Tedaj namrec robnih (n+1) x (m+1) kontrolnih tock sovpade z robnimi tockami povrsine.

Prednosti uporabe B-spline zapisa pred Bezierjevim je morda se bolj pomembna pri povrsinah. Ne-lokalnost Bezierjeve povrsine je pomanjkljivost pri deformiranju povrsin med postopki 3D modeliranja, nadalje lahko Bezierjeve "krpe" predstavljajo le enostavno topologijo. Zato je z B-spline zapisom mogoce popisati dalec bolj kompleksne povrsine z enim samim zapisom.



7 Literatura



[1] Watt Alan, Fundamentals of Three-Dimensional Computer Graphics, Addison-Wesley Publishing Company 1989

[2] Farin Gerald, Curves and Surfaces for Computer Aided Geometric Design, Academic Press inc.-Harcourt Brace Jovanovich Publishers, 1990

[3] Bu-qing Su & Ding-Yuan Liu, Computational Geometry-Curve and Surface Modeling, Academic Press inc.-Harcourt Brace Jovanovich Publishers, 1989