Projekt merjenje pretoka z Venturjevo cevjo po VDI/VDE2040 (de/en) (Venturi flowmeters)

Abstract

My task was to make a programme for measuring flow rates with Venturi Flow meters.

Basic data:

-dp...the measured difference in pressure

-density...the choice of the substance, its density, temperature and viscosity

-d,D...the cross-section dimensions of the measuring tool

The programme is devised in such a way that first it calculates the mass flow and then the volume flow through the tube.

dP Venturi Flow meters are the simplest and most reliable means of measuring flow . In an instrumentation market filled with vastly more complex options, venturi flow meters-an 18th Century solution-are still being selected for measuring flows in 21st Century process systems. Venturies use the basic Bernoulli equation which relates fluid velocity to pressure. Increase fluid velocity and the pressure decreases. By increasing the velocity by forcing the fluid through a throat of known diameter, and by measuring the resultant dP, we can calculate flow rate quite accurately.

Venturi flow meters have a number of key features which make them attractive for designing into a system:

Minimal Unrecoverable Pressure Loss-Venturies are usually chosen when losses must be minimized. Unrecoverable loss is about 15% of measured inlet-to-throat dP.

-No Moving Parts-No bearings

-Suitable for High Pressure/High Pressure/Low temperatures: -Venturies can be rated to any pressure.

-Rugged, Non-Invasive Design-No fragile, electronic components must be mounted on or near the venturi.

These features make them ideal for a variety of applications:

-Corrosive/Caustic Applications

-Can be easily manufactured in any material:
Monel, titanium, Teflon, Hastelloy, Naval Bronze

-Temperature extremes

Cryogenics (like LOX and Liquid Helium) or High Temperatures (exhaust gasses, molten metals)

-Contaminated, explosive, or radioactive fluids

Uvod

Pri predmetu Osnove in postopki konstruiranja smo dobili kot končno projektno nalogo izdelavo projekta za katerega smo dobili podano samo številko standarda in naslov.

Jaz sem si izbral nalogo s številko 13.21 merjenje pretoka z Venturjevo cevjo. Ta primer opisuje standard VDI/VDE 2040. Kot je razvidno že iz naslova naloge, je osnovna naloga tega standarda merjenje pretokov tekočin, plinov, par v širokem podrocju temperatur, tlakov in hitrosti, pri različnih lastnostih merilnih medijev.

Moja naloga je bila izdelati program za primer merjenja pretoka medija z Venturjevo cevjo.

Vhodni podatki so:

dp...izmerjena sprememba tlaka

gostota...izbira merilnega medija in s tem tudi gostoto, temperaturo, viskoznost

d,D...določitev dimenzije preseka merilnega elementa

Program najprej preračuna masni in nato še volumski pretok skozi cev.

Uvod v merjenje pretokov

Merjenje pretoka s postopkom merjenja razlike tlakov na dušilnih napravah je najbolj razširjen postopek v industrijski praksi merjenja pretokov. Po nekaterih ocenah merimo na tak način okoli 40 % vseh pretokov. Postopek omogoča merjenje pretokov tekočin, plinov in par v širokem področju temperatur, tlakov in hitrosti pri različnih lastnostih merilnih medijev.

Tako široka uporaba je posledica relativne enostavnosti konstrukcij in izvedb v primerjavi z drugimi postopki. Merjenje realiziramo brez premičnih ali rotirajočih delov,kjer bi se lahko pojavila umazanija ali usedline.

Postopek je tudi natančno obdelan v mednarodnih normah, kar omogoča primerljivost izvedb in rezultatov merjenj ter univerzalno uporabo.

Osnove delovanja

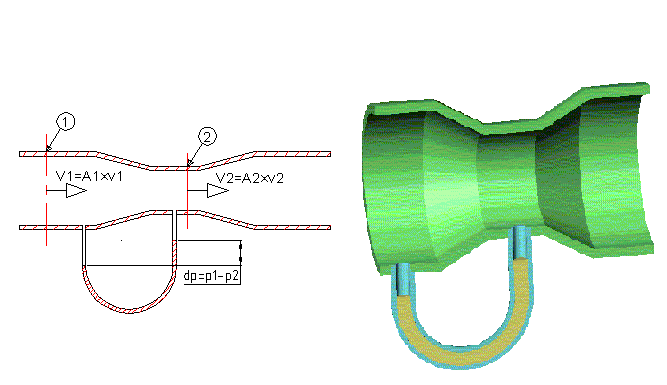
Pri merjenju pretoka z merjenjem razlike tlakov zožimo presek cevovoda z uporabo dušilnega elementa (naprave), kot kaže priložena skica. Po postopku merimo razliko tlakov dp=p1-p2, ki je odvisna od pretoka fluida. Naprava za merjenje je sestavljena iz treh delov, in sicer:

a) iz dušilnega elementa, nameščenega v cevovodu, zaradi katerega se pojavi razlika tlakov,

b) iz povezovalnih vodov, ki pripeljejo padec tlaka na merilno napravo, ter

c) iz merilne naprave- merilnika razlike tlaka, umerjenega v enotah prostorninskega pretoka.

Pri enakem prostorninskem pretoku se hitrost merilnega medija poveča na mestu dušenja (zožitve). Po zakonu vzdrževanja energije pride zaradi spremembe pretočne hitrosti do spremembe kinetične energije opazovanega elementa prostornine V v drugo obliko energije, kot na primer v potencialno položajno energijo, tlačno energijo ali pa se pojavi sprememba temperature merilnega medija.

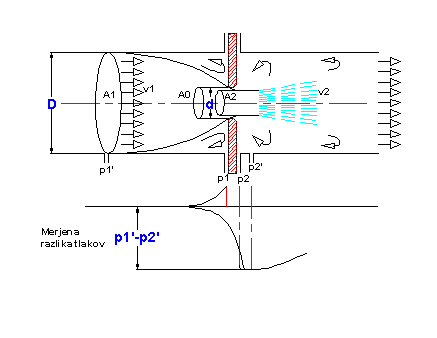
Iz vsega tega sledi znana Bernoullijeva enačba, zapisana za ti dve merjeni točki (pred in na sredini zožitve).V tej enačbi pomenijo indeksi (h) linijsko višinsko razliko,(g) težnostni pospešek, (v) hitrosti za dane točke prereza, (p) tlake za dane točke prereza, (gostota) gostota medija.

Merjenje pretoka iz razlike tlakov na dušilni napravi

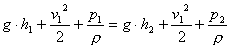
Postopek omogoča merjenja pretokov skoraj vseh vrst merilnih medijev pretakajočih se v cevovodih, kamor vgradimo zožitev v obliki dušilne naprave – zaslonke ali šobe, in kjer zaradi zožitve dobimo razliko tlaka, ki jo poznamo kot diferencialni, delotvorni, aktivni ali merilni tlak:dp=p1-p2. merilni tlak je merilo v časovni enoti po cevovodu pretakajočega se merilnega medija, je merilo pretoka, ki ga lahko določimo z merjenji dp. Pri postopku prikazujemo pretok v cevovodu ob pomoči pretočnega polja, ki ga lahko relativno dobro opišemo z Bernulljevo enačbo za idealne fluide.

Na običajnih merilnih mestih lahko dosežemo relativno točne rezultate merjenj, če so izpolnjeni naslednji pogoji:

-Pretakajoči se merilni medij mora zapolniti vse preseke cevovoda v bližini dušilne naprave

-Pretok mora biti stacionaren ali vsaj kvazistacionaren, kar pomeni , da se na merilnem mestu lahko le počasi spreminja. Nihanja merilnega medija, ki jih lahko povzročajo batni stroji, počasi se vrteči ventilatorji ali podobne naprave, občutno vplivajo na točnost merjenja in se jim zaradi tega moramo izogibati.

-Merilni medij mora biti v enem agregatnem stanju, kar pomeni, da brez posebnih ukrepov ne moremo meriti pretoka plinov in tekočin, v katerih so prisotna trda telesa, ali zmesi plinov in par s tekočinami. Ko se mediju poveča hitrost na merilnem mestu, se mu poveča tudi tlakkar je lahko pogoj za spremembo agregatnega stanja.

-Gostota merilnega medija neposredno pred dušilno napravo mora biti točno znana oziroma določljiva.

Pretočna enačba

Pri določanju pretočne enačbe bomo izhajali iz že prej omenjene Bernoulljeve enačbe za pretok. Upoštevali bomo profilni koeficient hitrosti (beta), ki je enak 1 za profile z enako hitrostjo po preseku, za vse druge oblike profilov pa je beta>1. Bolj kot je profil koničast, tem bolj narašča njegova vrednost.(večinoma je ta koef. med 1.04 in 1.06, pri laminarnih pretokih ima vrednost 2).

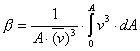
Tako z upoštevanjem dejstva, da je ta model vodoravno postavljen (h1=h2) in da sta masna pretoka v obeh presekih enaka, dobimo naslednjo okrajšano enačbo iz bivše Bernoulljeve:

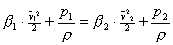
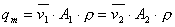
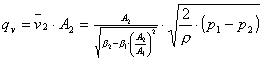
Ta enačba prikazuje pretoke idealnih fluidov po cevovodih, zato uvedemo spremenljivko a-(alfa)-(pretočno število)(Flow coefficient), ki je točno definirana s koeficienti kot so: kontrakcija, hitrostni profil in položaj mesta odvzema merilnega tlaka. Pretočno število a je brezdimenzijska vrednost. V literaturi in normah srečamo tudi pretočni koeficient C-(Coefficient of discharge).

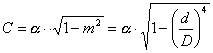
Do sedaj upoštevane enačbe so veljale samo za nestisljive medije, zato upeljemo novo neznanko E ekspanzijsko število, saj pri stisljivih medijih v dušilni napravi pride do povečanja prostornine plina in s tem do povečanja pretočne hitrosti. Posledica je povečanje tlaka, kar v pretočni enačbi masnega pretoka upoštevamo z uvedbo ekspanzijskega števila E<1 in tako dobimo novo pretočno enačbo:

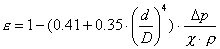
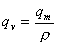
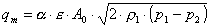
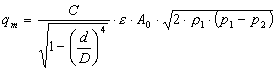
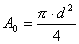
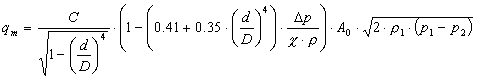
Za izračun te pretočne enačbe, ki velja za okrogle preseke cevovodov, vnesemo v okenca podatke, ki jih program zahteva. Vse vrednosti teh podatkov morajo biti v merilnih mejah, če želimo, da so dobljeni rezultati realni.

Klasično Venturjevo cev z odlitim in obdelanim pritočnim stožcem uporabljamo za cevovode premera 50mm<D<250mm z razmerjem prerezov 0,4<d/D<0,75za Rejnoldsova števila od 200000<Re<1000000 ter pretočnim koeficientom C=0,995(tolerance+-1%).

Ta program nam bo ob napačnem vnosu podatkov javil napako glede na postavljene mejne vrednosti. Na koncu bomo z pritiskom na gumb dobili želeni rezultat-pretok skozi cev.
V nadaljevanju je prikazan del kode programa zapisanega v jeziku HTML. Ta del nam izračuna izhodne podatke glede na vhodne podane ali izbrane vrednosti.

function izhod1(form) in function izhod2(form)
function izhod1(form)
{ var val1, val2, val3,visk,gostota;
form.masa.value = ((form.val1.value)*(form.val2.value)*(form.val3.value..........
form.gostota.value = material[form.material.selectedIndex][0];
form.visk.value = material[form.material.selectedIndex][1]; }
function izhod2(form)
{ var masa;
form.volumen.value =(form.masa1.value*form.gostota.value); }

Zaključek:

Izdelava te sminarske naloge je zahtevala veliko dela, saj je bilo potrebno najprej poiskati standard, ki je opisoval to nalogo, ga predelati in preučiti delovanje le tega, ter na koncu stestirati celotno stvar.
Naloga nam je nazorno pokazala področja ki jih mora konstrukter obvladati saj na tržisču sicer obstaja ogromno programov, vendar pa takega, kot ga potrebujemo, zelo redko najdemo. Zato si moramo znati tudi sami kaj sprogramirati in prav to mislim, da je bil namen te vaje.

Viri: