Gaussova kvadratura

Numericna integracija je metoda izracuna vrednosti integrala splosnih funkcij takrat, ko ni znana tocna analitisna resitev. Gauss-Legendrova kvadraturna formula omogoca hiter in natancen izracun integrala za splosne funkcije. Za razliko od ostalih metod (Simpsonova, trapezna, ...) ima ta integracija majhno stevilo izbranih tock, kar pospesi programe, ki racunajo veliko stevilo integralov.

Splosna enacba Gaussove kvadrature je

Integral funkcije f(x) se izracuna tako, da se v n tockah vzame vrednost funkcije , ki se jo pomnozi z z utezjo . Vsota tako obtezenih vrednosti funkcije je vrednost integrala. Pomembno je poudariti, da so meje integrala od -1 do 1, zato je potrebno pri drugacnih mejah uporabiti translacijo in skaliranje osnovne funkcije, predno uporabimo Gaussovo kvadraturo za izracun integrala. Integracija poteka torej simetricno. Red kvadrature doloca stevilo tock, ki so uporabljene pri izracunu integrala. V naslednji tabeli so podane kvadrature za posamezno stevilo tock:

 
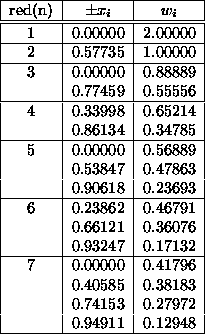
Table 1: Tocke za Gaussovo kvadraturo in utezi

Primer izracuna za funkcijo

za katero zelimo izracunati integral

in ima analiticno resitev 2.80.

• n = 2
  Imamo dve integracijski tocki pri Integral I izracunamo kot
  
  kar je 12.7% odstopanja od tocne resitve.
• n = 3
  Imamo tri integracijske tocke pri x = 0 in
  
  kar kaze na natacnost in hitrost kvadrature.

 
• Translacija in skaliranje