Analiza faznega zamika dveh signalov

Seminar

Abstract

Uvod

Analiza faznega zamika dveh signalov je uporabna na različnih področjih tehnike. Uporabna je na primer pri brezdotičnem merjenju oblike površine teles, analizi laserskih interferenčnih vzorcev, foto elastičnosti itd.
Ogledate si lahko sledeče www strani, kjer so prikazani instrumenti, ki uporabljajo podoben algoritem, kot je opisan tu: http://www.opton.co.jp/startp/start/indexe.html, http://www.warpfinder.com/shadowmoire.html, http://www.eois.com/, ...

Prednost fazne analize pred amplitudno je predvsem v tem, da je relativno neobčutljiva na nihanja jakosti signala. Pri tej metodi nas namreč zanima fazni zamik dveh signalov na posameznem mestu iz česar lahko posredno izračunamo višino merjene površine, spremembo frekvence med dvema signaloma itd.

Namen tega seminarja je prikazati delovanje algoritma in zanj izdelati program v java programskem jeziku, ki bo dostopen vsem uporabnikom interneta. V programu je možno proučevati vplive različnih parametrov na natančnost oziroma zanesljivost metode.

Opis algoritma

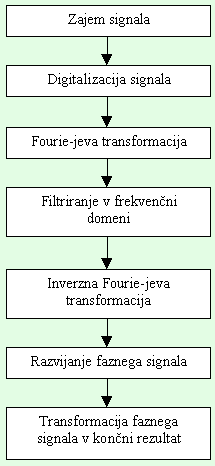
Algoritem analize faznega zamika je prikazan na diagramu spodaj:

Zajem signala in digitalizacija se pri merjenju profila površine vrši z uporabo digitalne kamere ter frame grabber-ja.

Fourie-jeva transformacija pretvori signal iz časovne v frekvencno domeno. Ker je to digitalna obdelava signalov, je potrebno uporabiti diskretno fourie-jevo transformacijo, ki ima sledečo enačbo:

Pri tem pomeni:

n …število točk,
v_k …k-ta točka signala v časovni domeni,
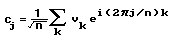
c_k …k-ta točka signala v frekvenčni domeni.

Kot je razvidno že iz same enačbe, je potrebno za izračun vsake točke v frekvenčni domeni sešteti zmnožke vseh točk z e^{i(2pi j/n)k} v časovni domeni. Zaradi tega postane izračun velikega števila točk dolgotrajen. Zato se običajno fourie-jeva transformacija vrši z uporabo FFT (fast fourier transform) algoritma, ki pa ima to slabost, da moramo uporabljati število točk, ki je mnogokratnik števila 2. (Priložen program uporablja navaden DFT algoritem).

Filtriranje v frekvenčni domeni se vrši z uporabo okna in sicer tako, da vrednosti funkcije okna pomnožimo z vrednostmi signala v frekvenčni domeni. Enačba okna je sledeča:

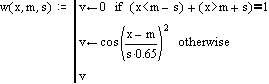
Pri čemer pomeni:

m …sredina okna,
s …polovična širina okna.

Graf, kjer je m=8 in s=3 prikazuje obliko okna. Z uporabo okna namreč iz signala izločimo vse frekvence razen tiste, ki nas zanima.

Inverzna fourie-jeva transformacija pretvori signal iz frekvenčne domene nazaj v časovno. Enačba diskretne inverzne transformacije je:

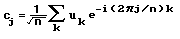
V naslednjem koraku se izračuna argumente vseh točk, ki smo jih dobili po inverzni transformaciji. Zaradi filtriranja v frekvenčni domeni imajo točke kompleksne vrednosti tudi po inverzni transformaciji. Razlika argumentov v posamezni točki dveh signalov pa predstavlja ravno njun fazni zamik.

Preden izračunamo fazno razliko med obema signaloma, pa je potrebno korigirati vrednosti argumentov posameznega signala. Ker vrne funkcija atan(x) le vrednosti na intervalu med -p in +p postane signal nezvezen (glej graf spodaj).

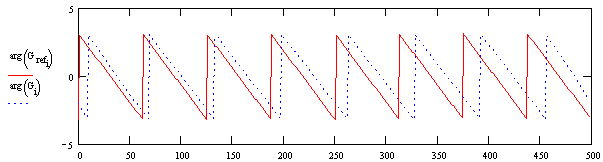
Zato je potrebno argumente signala razviti v nazaj pravilno obliko, tja povsod, kjer se zgodi preskok, je potrebno pristeti oziroma odsteti vrednost 2p. Tako dobimo lepo zvezno krivuljo (glej graf spodaj).

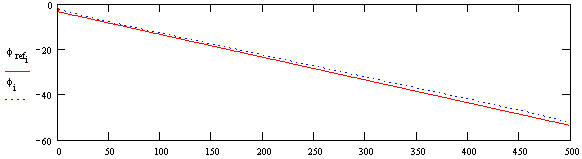
V naslednjem koraku je potrebno le se izračunati razliko med faznim potekom obeh signalov in kar dobimo, predstavlja fazni zamik enega signala relativno na drugega in sicer v vsaki posamezni točki.

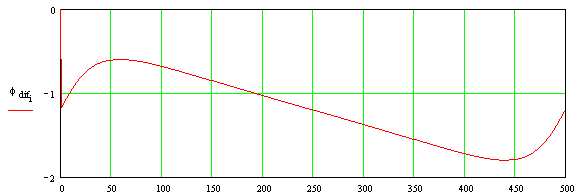
Graf zgoraj predstavlja fazni zamik dveh signalov, ki sta prikazana spodaj.

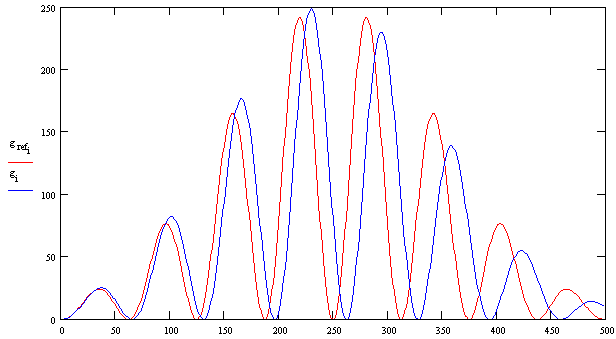
Frekvenca modrega signala je za 5% večja od rdečega signala, iz česar sledi, da se fazni zamik med obema linearno spreminja. To je razvidno tudi iz prejšnjega grafa. Do odstopanja prihaja le na robovih in sicer zaradi samega DFT algoritma in končne dolžine signalov.

Opis programa za analizo faznega zamika

Program ponazarja delovanje algoritma za analizo faznega zamika med dvema signaloma. Simulirana sta dva sinusna signala in sicer glede na vhodne parametre, ki jih lahko spreminjamo med samim delovanjem.
Parametri so sledeči:

• število točk,
• dolžina signala,
• perioda prvega signala,
• sprememba periode drugega signala v primerjavis prvim ter
• intenziteta šuma (šum ima normalno porazdelitev, parameter, ki ga vnašamo, je kar standardna deviacija).

Koda programa
Source of program