1. Abstract
Like a B-spline, a "Beta" spline curve or surface is specified by a set of points called control vertices. Althought these vertices do not generally lie on the generated curve or surface, their positions completely determine its shape. The vertices for a curve are an ordered sequence and are connected in succession to form a control polygon. The Beta spline basis is a local basis; that is, each Beta spline basis function has local support. The Beta spline formulation exploits the piecewise representation, in order to achieve local control, by defining each piece in terms of only a few nearby vertices. For Beta spline curves, each curve segment is controlled by only four of the control vertices and it is completely unaffected by all the other control vertices.
2. Uvod
Beta krivulje so dolocene z nizom tock, ki jih imenujemo kontrolne tocke. S pomocjo beta zlepkov lahko generiramo povrsino oziroma krivuljo, katera predstavlja ravninski primer. Na tej spletni strani so predstavljene osnovne lastnosti beta krivulj (ravninski primer), katere so zaradi svoje enostavne zgradbe zelo uporabne. Vhodni parametri so kontrolne tocke, katere dolocajo neko osnovno konturo dane beta krivulje. Pomembna lastnost beta krivulj je, da omogocajo lokalno kontrolo ( ena kontrolna tocka vpliva na sosednje stiri segmente) ter da omogočajo spremembo oblike krivulje samo z dvema parametroma (parameter "beta1" in "beta2").
3.Kratek matematicni opis
Krivulja je v osnovi razdeljena na segmente, ki so v bistvu polinomi tretjega reda. Vzdolz segmenta se spreminja zaloga vrednosti "u[k]", katera je vstopna vrednost v enacbo krivulje segmenta Q(i,k), ki je v bistvu parametricna funkcija.
Indeks "i" nakazuje i-ti segment beta krivulje, medtem, ko indeks "k" označuje k-to vrednost intervala katerega vrednost se giblje v intervalu od [0,1] z nekim korakom, od katerega je odvisna natancnost izrisa "beta" krivulje.
Parametra "beta1" in "beta2" sta definirana na naslednji nacin.
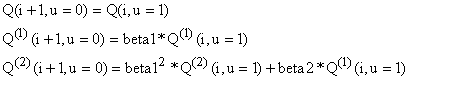
Kontrolni poligon je sestavljen iz kontrolnih tock V(j); j=0,1,2,...,m-1,m. Kontrolnih tock je torej m+1. Vsak segment je torej kontroliran s stirimi sosednjimi tockami, kar je definirano z naslednjo vrsto:
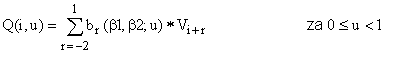
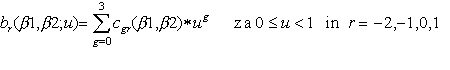
Pri spremembi parametra u od 0 do 1 je opisan celotni i - ti segment krivulje. Utezni faktorji so osnovne skalarne funkcije br(beta1,beta2; u) , r = -2,-1,0,1 , ovrednoteni pri doloceni vrednosti parametra u in oblikovnih parametrov beta1, beta2. S pomocjo parametrov beta1 in beta2 so definirani robni pogoji med dvema sosednjima segmentoma (Q(i-1,u=1) in Q(i,u=0)).
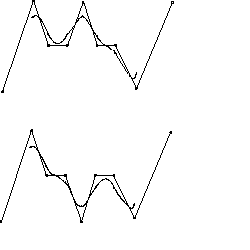
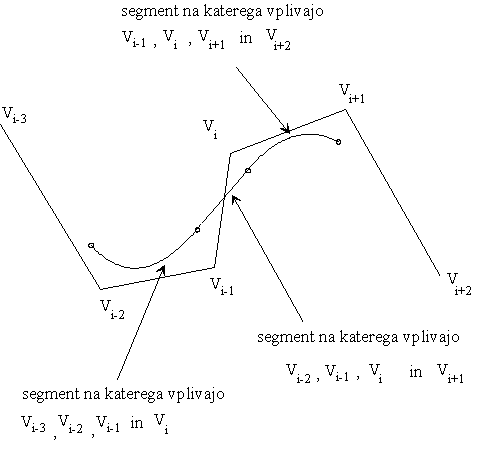
Na skici je prikazano, kako vpliva sprememba enega ogljisca na spremembo oblike krivulje (na stiri segmente).
Indeks "i+r" torej doloca ogljisca, katera vplivajo na segment krivulje Q(i)
4. Prakticni prikaz izrisa "beta" krivulj
Graficni program je napisan v programskem jeziku "Java", zato je potrebno za brezhibno delovanje programa imeti novejsi brskalnik (npr. Netscape Navigator, Internet Exploler 3.0...) , ki podpira Javo.
OPIS DELA PRI UPORABI GRAFICNEGA PROGRAMA ZA IZRIS "BETA KRIVULJ" :
a) S kliki miske na zaslom omogocimo vnose kontrolnih tock . Program samodejno poveze kontrolne tocke z daljicami.
b) Z vnosom pete tocke se izrisejo segmenti bete krivulje
c) Stevilo segmentov je za eno manjse od stevila kontrolnih tock
d) Z nadaljnim vnosom tock se izrisujejo tekoci segmenti beta krivulje.
e) S pomocjo dveh vnosnih polj, lahko vnasamo vrednosti parametrov beta1 in beta2, katera lahko zavzameta poljubno realno stevilo (bodisi pozitivno oziroma negativno).
f) Parametra beta1 in beta2 lahko spreminjamo tudi na ze izrisani krivulji.
g) S pomocjo gumba "Pocisti" lahko izvedemo dve operaciji:
- s prvim klikom nanj samo prekinemo povezavo med zadnjo izrisajoco se daljico. Ce zelimo risanje beta krivulje nadaljevati preprosto nadaljujemo z vnosom kontrolnih tock.
- z drugim klikom nanj dokoncno pocistimo graficni zaslon.
5. Uporabljena literatura
- Computer Graphics and Geometric Modeling Using Beta-splines; Brian A.Barsky
- JAVA, programiranje za internet; Uros Mesojedec (Pasadena,1996)
- JAVA za telebane; Aaron E. Walsh (Pasadena,1996)
- Odkrijte visual cafe; David A. Wall, Arthur Griffith (Atlantis, 1998)
- odlicna spletna stran www.sun.com
Avtor: Sebastjan Gregorsanec, 3.letnik UNI-KGS
Naslov: Mrtvice 48, 8273 Leskovec, SLOVENIA
Tel:386 (0)608-20-506
e-mail:anton.gregorsanec@guest.arnes.si
[NAVZGOR]