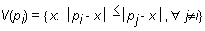
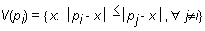
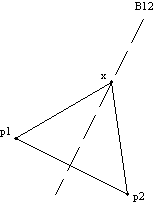
Naj bosta na ravnini samo dve točki p1 in p2. Naj bo premica B(p1, p2) = B12, ki pravokotno razdeli segment p1p2 na dva enaka dela. Potem je vsaka točka x na premici B12 enako oddaljena od točke p1, kakor tudi od točke p2. Velja: |p1x| = |p2x| (Slika 1).
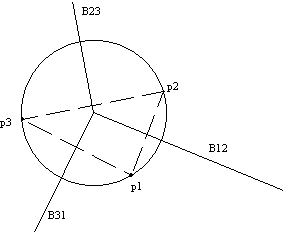
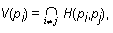
pri čemer je potrebno upoštevati presek preko vseh i in j, za katere
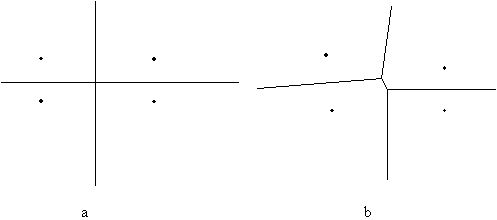
velja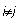 
. Iz enačbe sledi lastnost Voronoi diagrama: območja Voronoi
diagrama so konveksna, ker nastanejo kot presečišča večih polravnin.
Kadar so ta območja omejena, so to konveksni poligoni. Robovi se
imenujejo Voronoi robovi in temena Voronoi temena. Katerakoli točka na
Voronoi robu ima dve najbližji točki niza točk na ravnini, Voronoi teme
pa ima najmanj tri najbližje take točke.
V primeru štirih točk na ravnini, ki oblikujejo vogale kvadrata, je to
Voronoi diagram kot je prikazano na Sliki 3a. Voronoi teme je v tem
primeru četrte stopnje. Če se eno točko nekoliko premakne (Slika 3b),
postane diagram normalen. Prvi primer je izrojen zaradi centričnega
položaja štirih točk na ravnini.
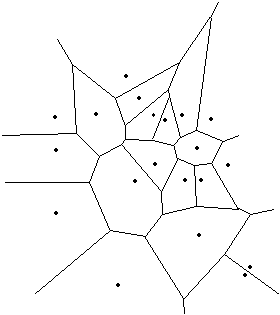
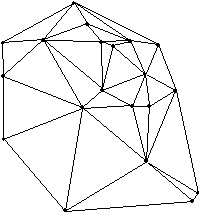
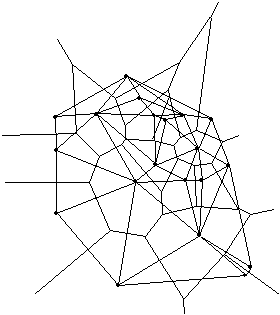
Za Delaunayevo triangulacijo veljajo lastnosti:
D1. D(P) je ravnočrtna dvojnost V(P), po definiciji.
D2. D(P) je triangulacija, če ne obstajajo štiri centrične
točke na ravnini: vsaka površina je trikotnik. Ploskve D(P) so
Delaunayevi trikotniki.
D3. Vsak trikotnik grafa D(P) ustreza temenu grafa V(P).
D4. Vsak rob grafa D(P) ustreza robu grafa V(P).
D5. Vsak vozel grafa D(P) ustreza območju grafa V(P).
D6. Meja D(P) je konveksna lupina
D7. Notranjost trikotnikov D(P) ne vsebuje nobenih točk niza P.
Za Voronoi diagram veljajo lastnosti:
V1. Vsako Voronoi območje V(pi) je konveksno.
V2. V(pi) je neomejen, če je pi na
konveksni lupini niza točk P.
V3. Če je Voronoi teme na stičišču V(p1),
V(p2) in V(p3), potem je v središču
kroga C(v), ki ga določajo točke p1,
p2 in p3.
V4. C(v) je očrtan krog pri Delaunayevi triangulaciji, ki ustreza v.
V5. V notranjosti C(v) ni nobene točke niza P.
V6. Če je pj najbližji pi,
potem je (pj,pi) rob triagulacije D(P).
V7. Če obstaja krog skozi točki pj in pi, ki ne vsebuje nobenih
drugih točk niza P, potem je (pj,pi) rob triangulacije D(P).
Začetek pregledovanja je tako rob, ki ga določata najnižja, najbolj desna točka in točka, ki je prva najbližja po naraščujočem kotu glede na os x (Slika 7).
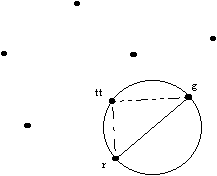
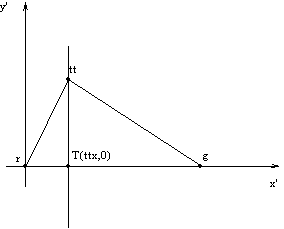
Prvi program, z imenom Princip tretje točke bere podatke iz datoteke Pod.txt in nato po teoriji tretje točke določi robove optimalne trikotniške mreže. Optimalna trikotnižka mreža je konveksna. Sestavljena je optimalnih trikotnikov, kjer naj bi veljalo pravilo maksimiziranja najmanjšega kota v trikotniku. To pravilo ni uporabljeno direktno, temveč po metodi principu tretje točke, kjer določimo središče očrtanega kroga in središče aktivnega roba (ta postopek ja že opisan v poglavju princip tretje točke).
V tem programu imamo dva podprograma. Podprogram tretja točka določuje
tretjo točko aktivnega roba ter izpisuje te točke v datoteko
Phigs.txt.
Drugi podprogram, z imenom Krog, določuje središče očrtanega kroga
trikotniku.
Drugi program Phigs.for prebere točke robov trikotnikov iz datoteke Phigs.txt ter jih s pomočjo grafične knjižnice PHIGS izriše v optimalno trikotniško mrežo.
program Princip tretje tocke
real x(1000),y(1000),p(1000,1000),alfa(1000)
real pxd,pyd,pxz,pyz
open(3,file='pod.txt')
open(4,file='phigs.txt')
open(5,file='brez.txt')
do i=1,1000
read(3,*,end=10)x(i),y(i)
p(i,1)=x(i)
p(i,2)=y(i)
sttock=i
write(*,*)p(i,1),p(i,2)
enddo
10 close(3)
**************************************************************************
c Dolocitev zacetne tocke (pxz,pyz).
pyz=y(1)
pxz=x(1)
do i=1,sttock-1
if (p(i+1,2).le.pyz)then
pxz=p(i+1,1)
pyz=p(i+1,2)
if(p(i+1,2).eq.pyz)then
if(p(i+1,1).lt.pxz)then
pxz=p(i+1,1)
pyz=p(i+1,2)
else
pxz=pxz
pyz=pyz
endif
endif
endif
enddo
write(*,*)'zacetna tocka je',pxz,pyz
***********************************************************
c Dolocitev druge tocke prvega trikotnika (pxd,pyd).
alf=180
do i=1,sttock
if(x(i).eq.pxz.and.y(i).eq.pyz)then
go to 20
endif
if(x(i).ge.pxz)then
alfa(i)=atan((y(i)-pyz)/(x(i)-pxz+0.000001))
else
alfa(i)=180+atan((y(i)-pyz)/(x(i)-pxz+0.000001))
endif
if(alfa(i).lt.alf)then
alf=alfa(i)
pxd=x(i)
pyd=y(i)
else
alf=alf
pxd=pxd
pyd=pyd
20 endif
enddo
write(*,*)'druga tocka je',pxd,pyd
**********************************************************
c pxz,pyz=zacetna tocka
c pyd,pyd=druga tocka
write(4,*)pxz,pyz
write(4,*)pxd,pyd
call tretja_t(pyz,pyd,pyt,pxz,pxd,pxt,sttock,x,y,pycrz)
do j=1,2*sttock
xz=pxz
yz=pyz
xt=pxt
yt=pyt
xd=pxd
yd=pyd
pxz=pxz1
pyz=pyz1
pxt=pxt1
pyt=pyt1
pxd=pxd1
pyd=pyd1
***********************************************************
pxz1=xz
pyz1=yz
pxd1=xt
pyd1=yt
call tretja_t(pyz1,pyd1,pyt1,pxz1,pxd1,pxt1,sttock,x,y,
1 pycrz)
if (pycrz.eq.1001)then
write(*,*)'ni leve zunaj 1'
goto 70
endif
write(5,*)'nekaj 1 t d z',xt,yt,xd,yd,xz,yz
write(5,*)'nekaj 1 pt pd pz',pxt1,pyt1,pxd1,pyd1,pxz1,
1 pyz1,pycrz
***********************************************************
70 pxz=xt
pyz=yt
pxd=xd
pyd=yd
call tretja_t(pyz,pyd,pyt,pxz,pxd,pxt,sttock,x,y,pycrz)
if (pycrz.eq.1001)then
write(*,*)'ni leve zunaj'
pxz=pxz1
pyz=pyz1
pxt=pxt1
pyt=pyt1
pxd=pxd1
pyd=pyd1
endif
write(5,*)'nekaj 2 t d z',xt,yt,xd,yd,xz,yz
write(5,*)'nekaj 2 pt pd pz',pxt,pyt,pxd,pyd,pxz,pyz,
1 pycrz
enddo
stop
100 write(*,*)'nekaj je narobe 100'
close(4)
end
**********************************************************
SUBROUTINE tretja_t(pyz,pyd,pyt,pxz,pxd,pxt,sttock,x,y,pycrz)
* subrotina nam izracuna:
* - kot rot. koord. sistema
* - doloci lego premice - orientiranost
* - rotira koord. sistem in vse tocke glede na nov koord. sistem
* - glede na levost tock, ocrta krog, sredisce, IZBERE 3. TOCKO
real d,e,fi,kpremice,x(1000),y(1000),pycrz
parameter(pi=3.14159265359)
c Izracun kota premice zacetnega aktivnega roba (fi)
kpremice=(pyz-pyd+0.000001)/(pxz-pxd+0.000001)
fi=atan(kpremice)*180/pi
c Dolocitev lege premice
if(pxz.ge.pxd.and.pyz.le.pyd)then
fi=180+fi
elseif(pxz.le.pxd.and.pyz.ge.pyd)then
fi=360+fi
elseif(pxz.gt.pxd.and.pyz.gt.pyd)then
fi=180+fi
elseif(pxz.lt.pxd.and.pyz.lt.pyd)then
fi=fi
endif
write(*,*)'***************************'
***********************************************************
c Rotacija koordinatnega sistema
d=cos(fi*pi/180)
e=sin(fi*pi/180)
pxdr=(pxd-pxz)*d+(pyd-pyz)*e
pydr=-((pxd-pxz)*e)+(pyd-pyz)*d
pxzr=(pxz-pxz)*d+(pyz-pyz)*e
pyzr=-((pxz-pxz)*e)+(pyz-pyz)*d
c Postavitev tock v nov koordinatni sistem.
pycrz=1001
do i=1,sttock
pxt=x(i) ! pxt,pyt=tretja tocka
pyt=y(i)
pxtr=(pxt-pxz)*d+(pyt-pyz)*e
pytr=-(pxt-pxz)*e+(pyt-pyz)*d
if(pytr.gt.0.001)then
call krog(pxzr,pyzr,pxdr,pydr,pxtr,pytr,pxcr,pycr)
if(pycr.lt.pycrz.and.pycr.ne.0.000)then
pycrz=pycr !min rot.y = pycrz
stevec=i
endif
endif
enddo
if (pycrz.eq.1001)then
write(*,*)'ni leve od znotraj'
goto 50
endif
write(*,*)'min rot. y',pycrz,x(stevec),y(stevec),stevec
pxt=x(stevec)
pyt=y(stevec)
***********************************************************
* zapis za PHIGS
write(4,*)pxz,pyz
write(4,*)pxt,pyt
write(4,*)pxt,pyt
write(4,*)pxd,pyd
50 return
end
***********************************************************
SUBROUTINE krog(x1,y1,x2,y2,x3,y3,xc,yc)
pr(xs,ys,x1,y1,x2,y2)=(ys-y1)*(x2-x1)-(xs-x1)*(y2-y1)
fp(v1,v2,w1,w2)=((v2*v2-v1*v1)+(w2*w2-w1+w1))
f(v1,v2,w1,w2)=fp(v1,v2,w1,w2)/(2.0*(v2-v1+0.000001))
g(v1,v2,w1,w2)=(w2-w1)/(v2-v1+0.000001)
ay(x1,x2,x3,y1,y2,y3)=(f(x1,x3,y1,y3)-f(x1,x2,y1,y2))/
1 (g(x1,x3,y1,y3)-g(x1,x2,y1,y2)+0.000001)
ax(x1,x2,x3,y1,y2,y3)=((x3*x3-x1*x1)+(y3-y1)*
2 ((y3+y1)-2*ay(x1,x2,x3,y1,y2,y3)))/(2.0*(x3-x1+0.000001))
if(pr(x1,y1,x2,y2,x3,y3).eq.0.0) then
else
if(x1.ne.x3) then
xc = ax(x1,x2,x3,y1,y2,y3)
yc = ay(x1,x2,x3,y1,y2,y3)
else
xc=ax(x2,x1,x3,y2,y1,y3)
yc=ay(x2,x1,x3,y2,y1,y3)
endif
rk=sqrt((x3-xc)**2+(y3-yc)**2)
endif
return
end
***********************************************************
program phigs
include 'phigsdef.f'
real WindowLimits(4)/0.0,15.0,0.0,15.0/
real ViewportLimits(4)/0.2,0.8,0.2,0.8/
real ClipLimits(4) /0.0,1.0,0.0,1.0/
real ViewMappingMatrix(3,3)
integer wkid, ErrorReturn, i,j,k,l
real qx(1000),qy(1000)
open(10,file='phigs.txt')
do i=1,1000
read(10,*,end=20)qx(i),qy(i)
k=i
enddo
20 write(*,*)'stevilo ogljisc =',k
close(10)
call popph(2,0)
wkid=2
call popwk(wkid," ",WK151280)
call pevmm(WindowLimits, ViewportLimits, ErrorReturn,
* ViewMappingMatrix)
do 50 i=1,3
do 60 j=1,3
write (*,*)ViewMappingMatrix(i,j)
60 continue
50 continue
call psplci(2)
call pslwsc(5)
call psln(plsoli)
call pswkw(wkid,0.0,1.0,0.0,1.0)
call pschh(0.005)
call pswkv(wkid,0.0,0.15,0.0,0.12)
******* Izris daljic kot polyline **********************************
call ppl(k,qx,qy)
pause
call pclwk(wkid)
c Zapre PHIGS (zakljuci z graficnim nacinom dela)
c ( PhigsCLosePHigs )
call pclph()
stop
end
[2] L. Kos, J. Duhovnik, Fakulteta za strojništvo, Ljubljana 1997.
[3] K. Mulmuley,Computational Geomtry: an Introduction Trough Rendomized Algorithms, Prentice -Hall, Inc.,1994
[4] Joseph O'Rourke,Computational Geomtry in C, Cambridge Universty Press, 1993
Vaše mnenje lahko pošljete na:
Andrej Marlin
Telephone: +386 61 1771-436