 FAKULTETA ZA STROJNIŠTVO
FAKULTETA ZA STROJNIŠTVO  Labolatorij LECAD
Labolatorij LECADFAKULTETA ZA STROJNIŠTVO
Labolatorij LECAD
Naslov seminarja:
(ORDERED DITHER)
Z metodo urejenega raztrosa (Ordered dither) lahko na črnobelih tiskalnikih in zaslonih ustvarimo učinek sivin, tako da variramo gostoto pojavljanja črnih pik. Izdelati je potrebno program, ki prebere rastersko datoteko s sivimi odtenki in z metodo urejenega raztrosa ustvari črnobelo sliko enake ločljivosti. Urejen raztros uporablja matriko v štirikotni ali šestkotni obliki.
Za izhodišče vzamemo črnobelo PPM (Portable PixMap format) datoteko, ki jo ustrezno transformiramo in rezultat zopet zapišemo v PPM datoteko.
Na črnobelih tiskalnikih in monitorjih imamo samo dve možni barvi: črno in belo. Slike pa so večinoma v 256 sivih odtenkih (0 je črna in 255 je bela barva). Če želimo take slike prikazati na črnobelih monitorjih in tiskalnikih, jih je potrebno ustrezno transformirati. Transformacija na način da bi spremenili prvo polovico sivih odtenkov od 0 do 127 v črno in od 128 do 255 v belo barvo večinoma ne da zadovoljivih rezultatov. Zato se je potrebno zanesti na druge metode. Ena izmed takih metod je urejen raztros. To je metoda ki s pomočjo različnih vzorcev in gostoto belih in črnih pik ustvari učinek sivin. Koliko odtenkov sive barve je možnih je odvisno od Threshold matrike. Ta matrika je lahko velikosti 2x2 pa tudi do 50x50 točk. Znane so nekatere matrike, ki dajo najbolj primerne vzorce v določenih okoliščinah.
Najbolj primeren slikovni format za transformacijo je PPM format (Portable PixMap). V nadaljevanju je predstavljena izdelava programa za tako transformacijo in tudi dobljeni rezultati.
Možno je tudi prenesti program na svoj PC: Ordered Dither.exe
Only two colors are possible when using black and white printers and monitors. Black and white. Pictures are shown in 256 greyscale shades (0 is black and 255 is white). This pictures have to be transformed if they want to be shown on black and white monitors and printers. Usually, transformation of the first half of greyscale shades from 0 to 127 into black and from 128 to 255 into white is not satisfactory. That is why we have to rely on other methods. One among methods is called Ordered Dither. This method creates with different patterns and density of white and black dots efect of grey shades. The number of grey shades depends on Threshold matrix. The size of matrix is from 2x2 to 50x50. Some matrixes are known which give most apropriate patterns in certain circumstances.
The most apropriate picture format for transformation is PPM format(Portable PixMap). Representation of elaboration of program for transformation and results is shown after this article.
It is also possible to use this program on your PC: Ordered Dither.exe
Iz poljubne barvne slike je potrebno ustvariti sliko v sivih odtenkih. Sivih odtenkov je lahko največ 256 (0-255). Tako sliko je potrebno shraniti v PPM formatu.
Nato je potrebno narediti program, ki bo izvedel naslednje:
Pomembno je da program pravilno prebere podatke iz PPM formata in jih tudi pravilno zapiše v PPM format. Program naj bo primeren za branje slik formata 1100x1100 pixlov in za transformacijo z Treshold matriko velikosti 50x50.
Rasterske slike so za generiranje zelo zahtevne, saj obstajajo različni formati kot so BMP, JPG, GIF, TIFF, PNG. Za navedene formate je potrebno generirati bitno datoteko v točno določenem formatu. Obstaja pa tudi rasterski format , ki ga lahko zapišemo v obliki ASCII v vseh jezikih, ki znajo pisati datoteke. Ta format se imenuje PPM (Portable PixMap) format.
PPM format odpremo lahko z vsakim urejevalnikom teksta. Zelo majhna rastrska slika PPM formata je na sliki1.

Slika 1: Barvna rastrska slika Primer.ppm
Zapis datoteke Primer.ppm prikazane na sliki 1 je naslednji:
P3 # Created by Paint Shop Pro 5 5 2 255 0 0 0 0 0 0 0 0 0 0 0 0 255 0 0 255 255 255 255 255 255 255 0 0 0 0 255 0 255 0
Vrstice v zapisu pomenijo naslednje:
Za vsako točko je določena trojica števil za rdečo zeleno in modro barvo (RGB). Z variacijo teh treh števil dobimo lahko vse preostale barve. Vsako število lahko varira od 0 do 255. Pri barvnih slikah so števila v trojki med seboj lahko različna. Črna barva ima vrednost (0 0 0), bela barva pa ima vrednost (255 255 255). Rastrska slika se začne ustvarjati v levem zgornjem kotu.
Barvno rastrsko sliko lahko spremenimo v sivo sliko. Slika na Primer.ppm v sivih odtenkih je prikazana na sliki 2.

Slika 2: Siva rastrska slika Primer.ppm
Zapis datoteke Primer.ppm prikazane na sliki 2 je naslednji:
P3 # Created by Paint Shop Pro 5 5 2 255 0 0 0 0 0 0 0 0 0 0 0 0 76 76 76 255 255 255 255 255 255 76 76 76 28 28 28 150 150 150
Iz zapisa se vidi da je tudi siva slika zapisana na enak način kot barvna slika. Vendar se tu pojavi sprememba v trojici števil, ki popišejo eno točko. Pri sivi sliki so števila v trojici vedno enaka in so v območju od 0 do 255. Ne more se spreminjati vsako posebej. To lastnost lahko s pridom izkoristimo pri transformaciji sive slike v črnobelo sliko.
Metoda urejenega raztrosa je ena izmed metod s katerimi ustvarimo učinek sivin pri črnobelih slikah. Ta učinek je pomemben pri črnobelih monitorjih in tiskalnikih. Učinek sivin ustvarimo z gostoto in vzorcem pojavljanja črnih in belih pik. To dosežemo tako da z Threshold matriko primerjamo matriko slike v sivih odtenkih. Če je vrednost trenutne točke večja od vrednosti Threshold matrike ji predpišemo vrednost za belo barvo (255), drugače pa vrednost za črno barvo (0).
Načelna programska koda je sledeča:
input: array[1..image_width] of array[1..image_height] of pixel; output: array[1..image_width] of array[1..image_height] of pixel; threshold: array[1..matrix_width] of array[1..matrix_heigh] of pixel; t: pixel; i, j: integer; threshold_dither: begin for y: integer ? 1, y ? y + 1, y < = image_height do j ? ((y - 1) mod matrix_heigh + 1; for x: integer ? 1, x ? x + 1, x < = image_width do i ? ((x - 1) mod matrix_ width + 1; if input[x][y] > threshold[x][y] then input[x][y] ? WHITE PIXEL; else input[x][y] ? BLACK PIXEL; endloop; endloop; end; end.
Z spreminjanjem Threshold matrike dobimo različne vzorce za popis sivin. Večja kot je matrika več stopenj vzorcev ima transformerana slika, in tako lahko bolj natanko popiše sive odtenke na originalni sliki. Število stopenj Threshold matrike izračunamo na sledeč način:
N = (Širina matrike * Višina matrike) + 1.
Primeri nekaterih Threshold matrik:
4x4 ordered dither matrix 4x4 horizontal lines matrix 4 4 4 4 1 9 3 1 11 2 3 4 13 5 15 7 5 6 7 8 4 12 2 10 9 10 11 12 16 8 14 6 13 14 15 16
4x4 magic square matrix 6x6 45 degree halftone matrix 4 4 6 6 1 7 10 16 15 9 17 32 22 30 12 14 3 5 7 1 3 19 35 23 8 2 15 9 13 5 11 27 26 33 13 11 6 4 31 21 29 16 10 18 20 36 24 8 2 4 28 25 34 14 6 12
6x6 90 degree halftone matrix M=8 (129 levels of gray) 6 6 16 8 30 19 13 20 31 35 64 59 51 41 42 52 60 61 65 70 78 88 87 77 69 68 18 8 5 9 21 29 58 34 28 19 20 29 35 53 71 95 101 110 109 100 94 76 12 4 1 2 10 28 50 27 14 12 13 16 30 45 79 102 115 117 116 113 99 84 17 7 3 6 14 27 40 18 5 4 3 10 21 43 89 111 124 125 126 119 108 86 26 16 11 15 22 32 39 17 6 1 2 11 22 44 90 112 123 128 127 118 107 85 34 25 24 23 33 36 49 26 9 7 8 15 31 46 80 103 120 122 121 114 98 83 57 33 25 24 23 32 36 54 72 96 104 105 106 97 93 75 63 56 48 38 37 47 55 62 66 73 81 91 92 82 74 67
Matrike je potrebno pred uporabo še ustrezno prilagoditi na stopnje med 0 in 255. Prava mejna stopnja se izračuna na sledeč način:
S = ( Trenutna vrednost Threshold matrike / N) * 255.
Primer lestvice sivin dobljene z Threshold matriko 4x4 ordered dither matrix je viden na sliki 3.

Slika 3: 17 stopenjska lestvica sivin
Na sliki 3 se lepo vidi spreminjanje vzorcev. Bolj ko se bližamo črni barvi, bolj so vzorci gosti.
Primer slike dobljene z urejenim raztrosom je viden na sliki4.
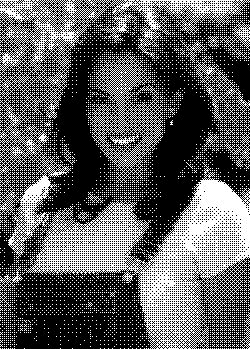
Slika 4: Primer slike dobljene z urejenim raztrosom
Aplikacija je izdelana v programskem okolju Delphi 3. Program je napisan v jeziku Pascal. Aplikacija je vidna na slikah 5 in 6. Zasnovana je tako da je razdeljena v tri polja:
Na aplikaciji se nahajat tudi gumb Start, za zagon transformacije, in gumb Exit za zaprtje aplikacije.
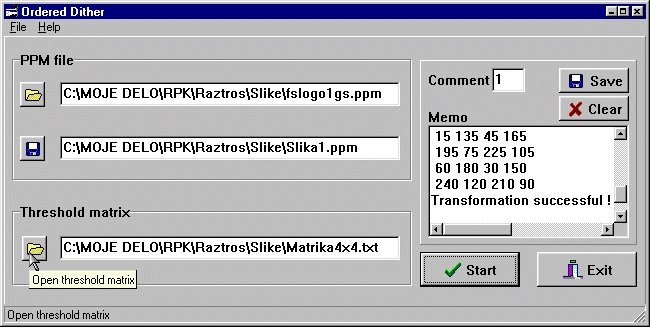
Slika 5: Aplikacija za urejen raztros

Slika 6: Vizitka aplikacije
Programska koda je napisana v jeziku Pascal. Poleg glavnega programa za urejen raztros vsebuje še vse potrebne definicije za: obliko okna, dialog Odpri, dialog Shrani, dialog Shrani kot, okno About ter vse elemente na aplikaciji.
V programski kodi so vz modro barvo napisani komentarji, ki naznanjajo začetek ali konec operacije, ki se izvede.
Programska koda je sledeča:
unit LogoMain;
interface
uses
Windows, Messages, Classes, Graphics, Forms, Controls, Menus, Dialogs,
StdCtrls, Buttons, ExtCtrls, ComCtrls, SysUtils, Mapi, About, LogoStrs;
type
TRaztrosForm = class(TForm)
AppMenu: TMainMenu;
FileMenu: TMenuItem; FileOpenItem: TMenuItem;
FileSaveItem: TMenuItem; FileExitItem: TMenuItem;
Help1: TMenuItem; AboutItem: TMenuItem;
OpenTreshold1: TMenuItem; SaveMemo1: TMenuItem;
OpenDialog: TOpenDialog; SaveDialog: TSaveDialog;
OpenDialog1: TOpenDialog; SaveDialog2: TSaveDialog;
SaveBtn: TSpeedButton; OpenBtn: TSpeedButton;SpeedButton1:TSpeedButton;
SaveBtn2: TSpeedButton; ExitBtn: TSpeedButton;
StartBtn: TBitBtn; Clear: TBitBtn;
SpeedPanel: TPanel; Panel1: TPanel;
StatusBar: TStatusBar;
GroupBox1: TGroupBox; GroupBox2: TGroupBox;
Edit1: TEdit; Edit2: TEdit; Edit3: TEdit; Edit5: TEdit;
Label3: TLabel; Label4: TLabel;
Memo1: TMemo;
procedure FormCreate(Sender: TObject);
procedure FileExit(Sender: TObject);
procedure FileOpen(Sender: TObject);
procedure FileOpen1(Sender: TObject);
procedure FileSaveAs(Sender: TObject);
procedure FileSaveAs2(Sender: TObject);
procedure About(Sender: TObject);
procedure ShowHint(Sender: TObject);
procedure StartBtnClick(Sender: TObject);
procedure ClearClick(Sender: TObject);
private
{ Private declarations }
public
{ Public declarations }
end;
var
RaztrosForm: TRaztrosForm;
Input: PIntArray;
Output: PIntArray;
Threshold: PIntArray;
implementation
{$R *.DFM}
{Zacetek programske kode}
var
F1, F2, F3: TextFile;
Col, Colf, ColMf, Row, Rowf, RowMf, pixel, point, com, i, j, k, l, m, n, d,
s, s1, o, p, x, y, z, w, level : Integer;
a, b, c, line, pix : String;
procedure TRaztrosForm.FormCreate(Sender: TObject);
begin
Application.OnHint := ShowHint;
end;
{Odpiranje in nastavitev mesta shranjevanja PPM datoteke}
procedure TRaztrosForm.FileOpen(Sender: TObject);
begin
if OpenDialog.Execute then begin
Edit1.Text:= OpenDialog.FileName;
end;
end;
procedure TRaztrosForm.FileSaveAs(Sender: TObject);
begin
if SaveDialog.Execute then begin
if FileExists(SaveDialog.FileName) then
if MessageDlg(FmtLoadStr(sOverwrite, [SaveDialog.FileName]),
mtConfirmation, mbYesNoCancel, 0) <> idYes then
Exit;
Edit2.Text := SaveDialog.FileName;
end;
end; {konec PPM datoteke}
{Odpiranje Treshold matrike}
procedure TRaztrosForm.FileOpen1(Sender: TObject);
begin
if OpenDialog1.Execute then begin
Edit3.Text:= OpenDialog1.FileName;
end;
end; {konec Treshold matrike}
{Shranjevanje Memo}
procedure TRaztrosForm.FileSaveAs2(Sender: TObject);
begin
if SaveDialog2.Execute then begin
if FileExists(SaveDialog2.FileName) then
if MessageDlg(FmtLoadStr(sOverwrite, [SaveDialog2.FileName]),
mtConfirmation, mbYesNoCancel, 0) <> idYes then Exit;
Memo1.Lines.SaveToFile(SaveDialog2.FileName);
end;
end; {konec Memo}
{Ostale finese}
procedure TRaztrosForm.FileExit(Sender: TObject);
begin
Close;
end;
procedure TRaztrosForm.About(Sender: TObject);
begin
AboutBox.ShowModal;
end;
procedure TRaztrosForm.ShowHint(Sender: TObject);
begin
StatusBar.SimpleText := Application.Hint;
end;
procedure TRaztrosForm.ClearClick(Sender: TObject);
begin
Memo1.Clear;
end; {konec finese}
{----------------Začetek glavnega programa !!!!!!------------------}
procedure TRaztrosForm.StartBtnClick(Sender: TObject);
begin
if Edit1.Text = '' then
FileOpen(Sender);
if Edit2.Text = '' then
FileSaveAs(Sender);
if Edit3.Text = '' then
FileOpen1(Sender);
AssignFile(F1, Edit1.Text); AssignFile(F2, Edit2.Text);
Reset(F1); Rewrite(F2);
AssignFile(F3, Edit3.Text);
Reset(F3);
Memo1.Lines.Add('Now transformation:');
Memo1.Lines.Add('Origin picture: ' + Edit1.Text);
Memo1.Lines.Add('Now picture: ' + Edit2.Text);
Memo1.Lines.Add('Matrix file: ' + Edit3.Text);
Readln(F3, b); Memo1.Lines.Add(b);
{Branje iz PPM datoteke v matriko}
com := StrToInt(Edit5.Text) + 1;
for i := 1 to com do begin
Readln(F1, a);
Writeln(F2, a);
end;
Writeln(F2, '# ORDERED DITHER !!! - ' + b + ' ');
Read(F1, Colf); Read(F1, Rowf);
Writeln(F2, FloatToStr(Colf) + ' ' + FloatToStr(Rowf) + ' ');
Readln(F1, a); Readln(F1, a); Writeln(F2, a);
s := Colf * Rowf;
GetMem(Input, (SizeOf(Integer) * s));
for Row := 1 to Rowf do begin
for Col := 1 to Colf do begin
Read(F1, pixel);
Input^[(Row - 1) * Colf + Col] := pixel;
Read(F1, d); Read(F1, d);
end;
end; {Konec branja PPM}
{Branje iz datoteke in ustvarjanje Treshold matrike ter zapis v Memo}
Read(F3, ColMf); Read(F3, RowMf);
Memo1.Lines.Add(FloatToStr(ColMf) + ' ' + FloatToStr(RowMf));
Readln(F3, b);
s1 := RowMf * ColMf;
GetMem(Threshold, (SizeOf(Integer) * s1));
for Row:= 1 to RowMf do begin
c := '';
for Col := 1 to ColMf do begin
Read(F3, point);
Threshold^[(Row - 1) * ColMf + Col] := point;
c := c + ' ' + FloatToStr(Threshold^[(Row - 1) * ColMf + Col])
end;
Memo1.Lines.Add(c);
end; {Konec branja Treshold}
{Začetek programa za Ordered Dither}
Memo1.Lines.Add('Multiply matrix:');
level := s1 + 1;
for Row:= 1 to RowMf do begin
c := '';
for Col := 1 to ColMf do begin
Threshold^[(Row - 1) * ColMf + Col] := Trunc((Threshold^[(Row - 1) *
ColMf + Col]/level)*255);
c := c + ' ' + FloatToStr(Threshold^[(Row - 1) * ColMf + Col])
end;
Memo1.Lines.Add(c);
end;
GetMem(Output, (SizeOf(Integer) * s));
for y := 1 to Rowf do begin
z := ((y - 1) mod RowMf) + 1;
for x := 1 to Colf do begin
w := ((x - 1) mod ColMf) + 1;
if Input^[(y - 1) * Colf + x] > Threshold^[(z - 1) * ColMf + w] then
Output^[(y - 1) * Colf + x] := 255
else
Output^[(y - 1) * Colf + x] := 0;
end;
end; {Konec programa za Ordered Dither}
FreeMem(Input, (SizeOf(Integer) * s));
FreeMem(Threshold, (SizeOf(Integer) * s1));
{Pisanje iz matrike v PPM datoteko}
m := Trunc((Rowf * Colf)/ 6);
n := (Rowf * Colf) Mod 6;
for k := 1 to m do begin
line := '';
for p := 1 to 6 do begin
pix := '';
for o := 1 to 3 do begin
pix := pix + FloatToStr(Output^[(k - 1) * 6 + p]) + ' ';
end;
line := line + pix;
end;
Writeln(F2, line);
end;
for l := 1 to n do begin
pix := '';
for o := 1 to 3 do begin
pix := pix + FloatToStr(Output^[6 * m + l]) + ' ';
end;
Write(F2, pix);
end;
CloseFile(F1); CloseFile(F2);{Konec pisanja v PPM}
FreeMem(Output, (SizeOf(Integer) * s));
Memo1.Lines.Add('Transformation successful !'); Memo1.Lines.Add(' ');
Beep;
end;
end.{Konec programske kode}
Program prebere PPM datoteko v kateri so sivi odtenki v vrednosti od 0 do 255. Zgradba PPM datoteke je bila že predhodno opisana. Del vhodne PPM datoteke je sledeče oblike:
P3 # Created by Paint Shop Pro 5 78 50 255 192 192 192 190 190 190 188 188 188 186 186 186 185 185 185 183 183 183 181 181 181 180 180 180 177 177 177 176 176 176 174 174 174 172 172 172 171 171 171 169 169 169 167 167 167 166 166 166 164 164 164 162 162 162 160 160 160 159 159 159 157 157 157 156 156 156 154 154 154 152 152 152 150 150 150 149 149 149 147 147 147 146 146 146 144 144 144 142 142 142 140 140 140 139 139 139 135 135 135 134 134 134 133 133 133 132 132 132 129 129 129 128 128 128 224 224 224 194 194 194 195 195 195 198 198 198 200 200 200 202 202 202 202 202 202 205 205 205 206 206 206 208 208 208 209 209 209 211 211 211 212 212 212 214 214 214 216 216 216 217 217 217 219 219 219 220 220 220 222 222 222 222 222 222 224 224 224 227 227 227
Po transformaciji z Threshold matriko dobimo izhodno PPM datoteko. Datoteka sedaj vsebuje samo vrednosti 0 in 255. Del datoteke je sledeč:
P3 # Created by Paint Shop Pro 5 # ORDERED DITHER !!! - 4x4 ordered dither matrix 78 50 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 0 0 0 255 255 255 255 255 255 255 255 255 0 0 0 255 255 255 255 255 255 255 255 255 0 0 0 255 255 255 255 255 255 255 255 255 0 0 0 255 255 255 0 0 0 255 255 255 0 0 0 255 255 255 0 0 0 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 255 0 0 0 0 0 0 255 255 255 0 0 0 255 255 255 0 0 0 255 255 255 0 0 0 255 255 255 0 0 0 255 255 255 0 0 0 255 255 255
Threshold matrika je v TXT datoteki zapisana na sledeč način:
4x4 ordered dither matrix 4 4 1 9 3 11 13 5 15 7 4 12 2 10 16 8 14 6
V prvi vrstici je komentar ki opiše vrsto matrike. Ta komentar se zapiše pod ostale komentarje v PPM datoteki. V drugi vrstici je napisana širina in višina matrike. V naslednjih vrstah sledijo vrednosti matrike.
V nadaljevanju so prikazani rezultati dobljeni z različnimi Threshold matrikami.
Osnovna slika je prikazana na sliki 7.

Slika 7: Osnovna slika
Na sliki 8 je prikazana slika dobljena z matriko 2x2 ordered dither matrix , ki je sledeče oblike:
1 3
4 2
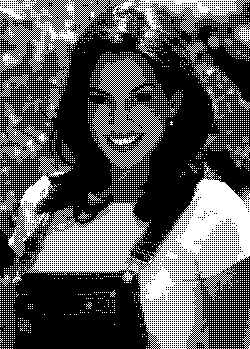
Slika 8: 2x2 ordered dither matrix
Na sliki 9 je prikazana slika dobljena z matriko 4x4 ordered dither matrix, ki je sledeče oblike:
1 9 3 11
13 5 15 7
4 12 2 10
16 8 14 6
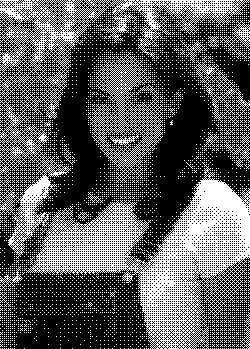
Slika 9: 4x4 ordered dither matrix
Na sliki 10 je prikazana slika dobljena z matriko 4x4 horizontal lines matrix, ki je sledeče oblike:
1 2 3 4
5 6 7 8
9 10 11 12
13 14 15 16

Slika 10: 4x4 horizontal lines matrix
Na sliki 11 je prikazana slika dobljena z matriko 4x4 magic square matrix, ki je sledeče oblike:
1 7 10 16
12 14 3 5
8 2 15 9
13 11 6 4
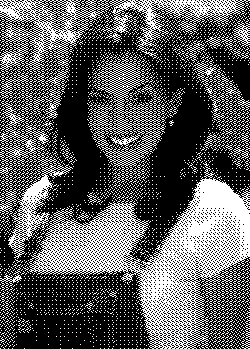
Slika 11: 4x4 magic square matrix
Na sliki 12 je prikazana slika dobljena z matriko 6x6 45 degree halftone matrix, ki je sledeče oblike:
15 9 17 32 22 30
7 1 3 19 35 23
13 5 11 27 26 33
31 21 29 16 10 18
20 36 24 8 2 4
28 25 34 14 6 12

Slika 12: 6x6 45 degree halftone matrix
Na sliki 13 je prikazana slika dobljena z matriko 6x6 90 degree halftone matrix, ki je sledeče oblike:
30 19 13 20 31 35
18 8 5 9 21 29
12 4 1 2 10 28
17 7 3 6 14 27
26 16 11 15 22 32
34 25 24 23 33 36

Slika 13: 6x6 90 degree halftone matrix
Na sliki 14 je prikazana slika dobljena z matriko M=3 (19 levels of gray), ki je sledeče oblike:
9 7 8 10 12 11
6 1 2 13 18 17
5 4 3 14 15 16

Slika 14: M=3 (19 levels of gray)
Na sliki 15 je prikazana slika dobljena z matriko M=4 (33 levels of gray), ki je sledeče oblike:
14 12 13 16 19 21 20 17
5 4 3 10 28 29 30 23
6 1 2 11 27 32 31 22
9 7 8 15 24 26 25 18
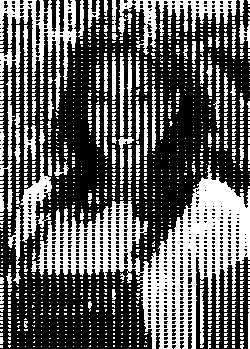
Slika 15: M=4 (33 levels of gray)
Na sliki 16 je prikazana slika dobljena z matriko M=8 (129 levels of gray), ki je sledeče oblike:
64 59 51 41 42 52 60 61 65 70 78 88 87 77 69 68
58 34 28 19 20 29 35 53 71 95 101 110 109 100 94 76
50 27 14 12 13 16 30 45 79 102 115 117 116 113 99 84
40 18 5 4 3 10 21 43 89 111 124 125 126 119 108 86
39 17 6 1 2 11 22 44 90 112 123 128 127 118 107 85
49 26 9 7 8 15 31 46 80 103 120 122 121 114 98 83
57 33 25 24 23 32 36 54 72 96 104 105 106 97 93 75
63 56 48 38 37 47 55 62 66 73 81 91 92 82 74 67

Slika 16: M=8 (129 levels of gray)
Na sliki 17 je prikazana slika dobljena z matriko Corrected M8 alfa 0.5 , ki je sledeče oblike:
30 23 20 15 16 17 28 31 35 42 45 50 49 48 37 34
22 14 8 3 4 5 9 25 43 51 57 62 61 60 56 40
21 13 7 2 1 6 10 26 44 52 58 63 64 59 55 39
29 24 19 12 11 18 27 32 36 41 46 53 54 47 38 33

Slika 17: Corrected M8 alfa 0,5
Na sliki 18 je prikazana slika dobljena z matriko Corrected Classical Screen - 0 Degee , ki je sledeče oblike:
35 30 18 22 31 36
29 15 10 17 21 32
14 9 5 6 16 20
13 4 1 2 11 19
28 8 3 7 24 25
34 27 12 23 26 33
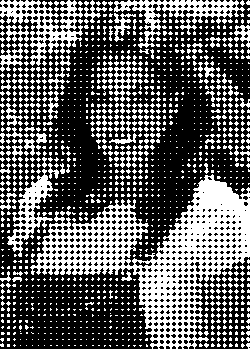
Slika 18: Classical Screen - 0 Degee
Na sliki 19 je prikazana slika dobljena z matriko Line Screen , ki je sledeče oblike:
36 34 32 31 33 35
24 22 20 19 21 23
12 10 8 7 9 11
6 4 2 1 3 5
18 16 14 13 15 17
30 28 26 25 27 29

Slika 19: Line Screen
Na sliki 20 je prikazana slika dobljena z matriko Spiral-Dot Screen, ki je sledeče oblike:
21 22 23 24 25
20 7 8 9 10
19 6 1 2 11
18 5 4 3 12
17 16 15 14 13
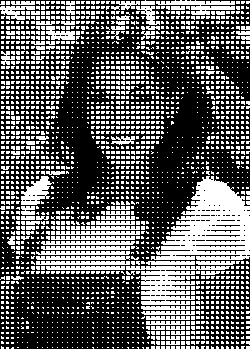
Slika 20: Spiral-Dot Screen
Izdelani program transformera sliko s sivimi odtenki v sliko z črnobelimi pikami po načinu urejenega raztrosa. Program da rezultate, ki ustrezajo že znanim rezultatom, zato deluje pravilno. Uporaben je takorekoč za vse slike.
Znane možne težave:
Vaša vprašanja in mnenja lahko pošljete na e-mail: jure.comino@kiss.uni-lj.si
Jure Comino
Ig 126
1292 Ig
Slovenia
+386 61 662-092