10.10 Meglenje slike (blur)

Tomaž Bučar

15.avgust, 1999

Abstract:

One of the most powerful tehniques in all of image processing is convolution. At the heart of this operation is the convolution mask or filter. Blurring filters smooth an image by reducing the contrast between adjacent pixels. i.e. the noise is reduced in those parts of an image, where the change in intensity from one pixel to the next is high. The following program Tblur blurs color PPM format images and grey scale PGM format images, which must be written in ASCII code.

Kazalo:

1. Uvod
2. Teoretične osnove
  2.1. Grafična formata PGM inPPM
  2.2. Konvolucija
  2.3. Filtri za zameglitev
3. Opis programa Tblur
4. Zagon programa Tblur in primeri
5. Literatura


 

1. Uvod

Začetki računalniške obdelave rasterskih slik segajo približno 40 let nazaj, ko so se pri raziskovanju planetov pojavile zahteve po boljši kvaliteti posnetih fotografij. To poročilo prikazuje teoretične osnove zameglitve rasterske slike, ki je ena od pomembnih operacij digitalnega procesiranja.

Posebne učinke dosežemo s pomočjo različnih filtrov. Za navadno zameglitev slike se uporablja preprost filter, s katerim zmanjšamo šum v tistih delih slike, kjer prihaja do ostrih barvnih sprememb. Ostri barvni prehodi se zgladijo s povprečenjem barv točk.

V nadaljevanju predstavljen program Tblur, ki si ga lahko presnamete na svoj računalnik, zamegli rastersko sivinsko ali barvno sliko formata PGM (Portable GreyMap) in PPM (Portable PixelMap). Ta dva grafična formata, napisana v ASCII obliki, sta zelo primerna za obdelavo bitnih slik.
 

2. Teoretične osnove

2.1. Grafična formata PGM in PPM

Rastersko sliko lahko zapišemo v različne formate, med katerimi se najbolj uporabljajo GIF, JPEG, TIFF, BMP, EPS in drugi. Obstajta pa tudi grafična formata, ki ju lahko zapišemo v ASCII obliki in sta zelo enostavena za generiranje (PGM in PPM).
 

PGM (Portable GreyMap)


Slika 1: Rasterska sivinska slika

Izgled datoteke predstavljene rasterske slike zapisane v formatu PGM je:

P2
# Created by Paint Shop Pro 5
4 4
255
200 123 45 234
0 167 255 67
234 156 23 189
98 111 178 134

Prve štiri vrstice datoteke predstavljajo glavo grafičnega formata PGM. Znak P2 v prvi vrstici je potreben za razpoznavo tipa datoteke. Namesto znaka P2 se lahko pojavi tudi znak P5. Znak P2 pove, da gre za ASCII obliko zapisa, medtem ko bi znak P5 predstavljal binarno obliko.V drugi vrstici je napisan komentar, pred katerim mora biti obvezno znak #, da ga prevajalnik preprosto preskoči. V tretji vrstici sta podatka o širini in višini slike. Prvo število pove, da je slika 4 točke široka, drugo število pa pove, da je slika 4 točke visoka. V naslednji vrstici je število 255, ki predstavlja največjo svetlost barve in je v mejah od 0 do 255. Vrednost 0 pomeni, da je barva izklopljena, vrednost 255 pa pomeni, da je barva maksimalno prisotna.
V naslednjih vrsticah so podatki o barvi posamezne točke oziroma pixla. Ker je format PGM namenjen za sivinske slike, pripada vsaki točki samo eno število. To število ima vrednosti od 0 do 255, kjer ima črna barva vrednost 0, bela pa 255. Vmesne vrednosti pa predstavljajo sivinske barve pri prehodu iz črne v belo.Rastrska slika se začne sestavljati v levem zgornjem kotu in se zapolnjuje tako, kot si sledijo števila.
 

PPM (Portable PixelMap)


Slika 2: Rasterska barvna slika

Izgled datoteke predstavljene rasterske slike zapisane v formatu PPM je:

P3
# Created by Paint Shop Pro 5
4 4
255
0 0 0 250 134 40 255 255 255 120 145 102
76 126 167 215 55 25 28 146 164 127 56 100
180 182 202 45 65 69 162 185 135 29 56 250
150 99 32 174 156 123 47 11 56 210 103 147

Prve štiri vrstice datoteke predstavljajo glavo grafičnega formata PPM. Znak P3 v prvi vrstici je potreben za razpoznavo tipa datoteke. Namesto znaka P3 se lahko pojavi tudi znak P6. Znak P3 pove, da gre za ASCII obliko zapisa, medtem ko bi znak P6 predstavljal binarno obliko.V drugi vrstici je napisan komentar, pred katerim mora biti obvezno znak #, da ga prevajalnik preprosto preskoči. Tako kot pri grafičnem formatu PGM sta v tretji vrstici podatka o širini in višini slike. Prvo število pove, da je slika 4 točke široka, drugo število pa pove, da je slika 4 točke visoka. V naslednji vrstici je število 255, ki predstavlja največjo svetlost barve in je v mejah od 0 do 255. Vrednost 0 pomeni, da je barva izklopljena, vrednost 255 pa pomeni, da je barva maksimalno prisotna.
Tudi pri formatu PPM so v naslednjih vrsticah zapisani podatki o barvi posamezne točke oziroma pixla. Ker je format PPM namenjen za barvne slike, pripadajo vsaki točki tri števila, in sicer za rdečo, zeleno in modro barvo. Tako nam kombinacija števil (0 0 0) predstavlja črno barvo, kombinacija (255 255 255) pa belo barvo. Rdečo barvo nato dobimo s kombinacijo (255 0 0), modro (0 0 255) in zeleno (0 255 0). Rastrska slika se začne sestavljati v levem zgornjem kotu in se zapolnjuje tako, kot si sledijo števila.
 

2.2. Konvolucija

Operacije, ki jih izvajamo na točkah oziroma pixlih rasterske slike pri procesiranju, se delijo v tri skupine:" točkovne operacije" (point operations), " sosedne operacije" (neighborhood operations) in "oblikovne operacije" (morphological operations). Najbolj pomembna  in mogočna "sosedna operacija" je konvolucija. Konvolucija v digitalni sliki pomeni, da ožje območje točk združimo skupaj z namenom, da bi dosegli željene rezultate. Matematični zapis konvolucije ima veliko oblik, uporabna pa je za izvrševanje mnogih funkcij. Splošno enačbo konvolucije lahko zapišemo na sledeč način:

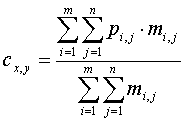
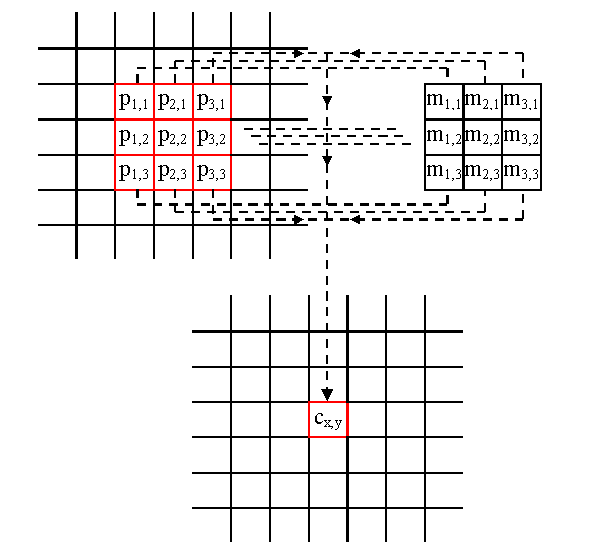
Slika 3 prikazuje operacijo konvolucije v slikovni obliki. Bistvo te operacije je konvolucijska maska ali jedro, prikazana s črko M na tej sliki. Tej konvolucijski maski lahko rečemo tudi filter, ki ima ustrezne elemente označene z m(i,j) in svojo dimenzijo m×n. Kot je prikazano na sliki, je vsak element v filtru pomnožen z ustrezno vrednostjo točke vhodne slike P. Rezultate množenja seštejemo in nato delimo z vsoto elementov filtra. Rezultat deljenja je točka oziroma pixel c(x,y) v obdelani sliki C.


Slika 3: Prikaz operacije konvolucije

Za zgornji primer je izpeljana enačba konvolucije sledeče oblike:

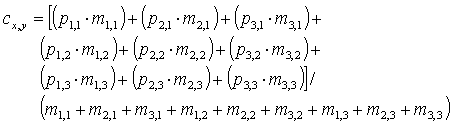
Operacija konvolucije zahteva veliko računsko moč. Za preračun ene točke je potrebno izvesti m×n množenj, m×n-1 seštevanj in eno deljenje. Za ivedbo konvolucije s filtrom 3×3 na barvni sliki 1024×1024 točk je tako potrebnih 27 milijonov množenj, 24 milijonov seštevanj in 3 milijone deljenj. Če pa velikost filtra povečamo na 5×5 ali 8×8 pri še večjih slikah, potem postanejo številke astronomsko visoke.
 

2.3. Filtri za zameglitev

Za razumevanje delovanja filtrov za zameglitev moramo poznati pojem visoke in nizke frekvence slike. V sliki, ki ima svetle bele like na črnem ozadju, prehod med robovi belih likov in črnega ozadja ustvarja visoko frekvenco. Vrednost točke se torej spreminja od visokih do nizkih vrednosti zelo hitro. Če pa se barve skozi površino spreminjajo počasi, kot npr. nebo pri sončnem zahodu, ima slika nizko frekvenco. Prav spreminjanje karakteristične frekvence slike je bistvo digitalnega procesiranja.
Filtri za zameglitev so nizkopasovni filtri. Enostaven filter velikosti 3×3 je prikazan na sliki 4. Izhodna točka ali pixel je enostavno povprečje vhodnih sosednih točk. Na območjih kjer je nizka frekvenca (vrednosti točk so približno enake), je vrednost izhodne točke skoraj identična vhodnim točkam. Nizkopasovni filter torej nizkih frkvenc ne spremeni. V področjih visoke frekvence pa se s povprečenjem točk zmanjšajo ostri barvni prehodi.


Slika 4: Enostaven filter za zameglitev 3×3


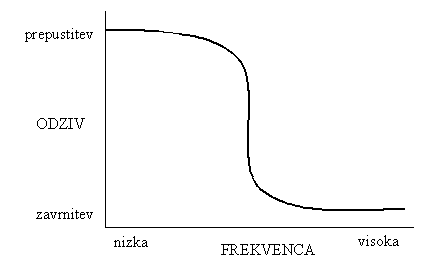
Slika 5: Odziv filtra za zameglitev

Na sliki 5 je prikazan odziv omenjenega filtra, ki prepušča nizke frekvence, visokih pa ne. Z zmanjšanjem visokih frekvenc, ki definirajo ostre robove, pravimo, da slika postane zamegljena.
Filtri za zameglitev so lahko tudi večjih dimenzij, kar povzroči večjo zameglitev slike. V mnogih grafičnih programih so na voljo tudi posebni filtri, ki ustvarijo videz gibanja (Motion blur) ali pa filtri za krožno zameglitev slike. Pri slednjem je učinek podoben, kot bi med fotografiranjem zavrteli fotoaparat ali spreminjali goriščno razdaljo objektiva. Največ pa se uporablja filter, katerega jakost določimo sami. Pri tem filtru dosežemo željen učinek na sliki s povprečenjem barv, ki se prilegajo Gaussovi krivulji (Gaussian blur).
 

3. Opis programa Tblur

Aplikacija je izdelana v programskem okolju Fortran PowerStation 4.0 in napisana v jeziku Fortran. Program najprej prebere datoteko grafičnega formata PGM ali PPM, nato uporabi metodo povprečenja sosednih točk in na koncu izdela datoteko ustreznaga  grafičnega formata. V nadaljevanju so prikazani bistveni elementi programske kode, ki so potrebni za razumevanje in pravilno delovanje programa. Celotno programsko kodo, napisano v omenjenem programskem jeziku, pa lahko tudi presnamete na svoj računalnik: tblur.txt

Program ob zagonu od uporabnika zahteva, da izbere zameglitev sivinske ali barvne slike. Po izbiri je potrebno vpisati ime vhodne datoteke grafičnega formata PGM (sivinska slika) ali PPM (barvna slika). Program na začetku prebere glavo datoteke in preveri pravilnost formata, nato pa prebere podatke o točkah. Branje poljubne datoteke omenjenih dveh formatov rešimo na naslednji način:

130   WRITE (*,12) 'Napisi ime vhodne datoteke tipa *.pgm'
12     FORMAT (/A41/)
         READ(*,*) VFILE
         OPEN(1,FILE=VFILE,STATUS='OLD')
         READ(1,*) TD, KOM
         IF ((TD=='P2').AND.(KOM=='#')) THEN
         READ (1,*) W,H,S
         ELSE
         WRITE(*,*) 'Napisali ste nepravilen tip datoteke!'
         GOTO 130
         END IF
         READ(1,*,END=140) (vt(k),k=1,n)
140   CONTINUE
         CLOSE (1)

Za nadaljno računanje s točkami je ugodno prebrane točke zapisati v obliki matrike. V glavi datoteke sta zapisani višina (H) in širina (W) slike, ki nam omogočita enostaven zapis tabele. Pri barvni sliki je matrika večja, saj vsaki točki pripadajo tri števila:
- sivinska slika

DO j=1,W
    DO i=1,H
        VTM(i,j)=VT(j+(i-1)*W)
    END DO
END DO

- barvna slika

DO j=1,(3*W)
    DO i=1,H
        VTM(i,j)=VT(j+(i-1)*(3*W))
    END DO
END DO

Dobljena matrika 5×5 za format PGM izgleda:

VTM(i-2,j-2)VTM(i-2,j-1)VTM(i-2,j)VTM(i-2,j+1)VTM(i-2,j+2)
VTM(i-1,j-2)VTM(i-1,j-1)VTM(i-1,j)VTM(i-1,j+1)VTM(i-1,j+2)
VTM(i,j-2)VTM(i,j-1)VTM(i,j)VTM(i,j+1)VTM(i,j+2)
VTM(i+1,j-2)VTM(i+1,j-1)VTM(i+1,j)VTM(i+1,j+1)VTM(i+1,j+2)
VTM(i+2,j-2)VTM(i+2,j-1)VTM(i+2,j)VTM(i+2,j+1)VTM(i+2,j+2)

Pri barvnih slikah pa je matrika za eno barvo nekoliko drugačna:

VTM(i-2,j-6)VTM(i-2,j-3)VTM(i-2,j)VTM(i-2,j+3)VTM(i-2,j+6)
VTM(i-1,j-6)VTM(i-1,j-3)VTM(i-1,j)VTM(i-1,j+3)VTM(i-1,j+6)
VTM(i,j-6)VTM(i,j-3)VTM(i,j)VTM(i,j+3)VTM(i,j+6)
VTM(i+1,j-6)VTM(i+1,j-3)VTM(i+1,j)VTM(i+1,j+3)VTM(i+1,j+6)
VTM(i+2,j-6)VTM(i+2,j-3)VTM(i+2,j)VTM(i+2,j+3)VTM(i+2,j+6)

Naslednji korak je izvedba operacije konvolucije s katero dosežemo učinek zameglitve. S programom lahko zameglimo izbrano sliko na tri različne načine. Pod izbiro Blur uporabimo enostaven filter velikosti 3×3, kjer imajo vsi elementi filtra vrednost 1. Pri izbiri Blur more je učinek zameglitve opaznejši, saj uporabimo filter velikosti 5×5, kjer imajo vsi elementi vrednost 1. V praksi se največ uporablja Gaussian blur, katerega jakost običajno določimo sami. V programu Tblur pa je uporabljen filter velikosti 5×5, kateremu priredimo vrednosti, ki se prilegajo Gaussovi krivulji. V nadaljevanju so prikazani uporabljeni filtri:

Filter 3×3:
1
1
1
1
1
1
1
1
1

Filter 5×5:
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1

Filter 5×5 (Gauss):
0.175
0.2
0.25
0.2
0.175
0.2
0.375
0.5
0.375
0.2
0.25
0.5
1
0.5
0.25
0.2
0.375
0.5
0.375
0.2
0.175
0.2
0.25
0.2
0.175

Algoritem povprečenja sosednih točk (konvolucija) za filter 5×5 (Gauss) izdelamo na sledeč način:
- sivinska slika

DO j=1,W
   DO i=1,H
        IT(i,j)=(VTM(i,j)+0.5*(VTM(i,j+1)+VTM(i,j-1)+VTM(i-1,j)+VTM(i+1,j))+
                   +0.375*(VTM(i-1,j-1)+VTM(i+1,j-1)+VTM(i-1,j+1)+VTM(i+1,j+1))+
                   +0.25*(VTM(i-2,j-2)+VTM(i-2,j+2)+VTM(i+2,j-2)+VTM(i+2,j+2))+
                   +0.2*(VTM(i-2,j)+VTM(i,j+2)+VTM(i,j-2)+VTM(i+2,j))+
                   +0.175*(VTM(i-2,j-1)+VTM(i-1,j-2)+VTM(i-2,j+1)+VTM(i-1,j+2)+
                   +VTM(i+1,j-2)+VTM(i+2,j-1)+VTM(i+2,j+1)+VTM(i+1,j+2)))/7.8
   END DO
END DO

- barvna slika

! povprečenje rdeče barve
DO j=1,3*W,3
   DO i=1,H
        IT(i,j)=(VTM(i,j)+0.5*(VTM(i,j+3)+VTM(i,j-3)+VTM(i-1,j)+VTM(i+1,j))+
                   +0.375*(VTM(i-1,j-3)+VTM(i+1,j-3)+VTM(i-1,j+3)+VTM(i+1,j+3))+
                   +0.175*(VTM(i-2,j-6)+VTM(i-2,j+6)+VTM(i+2,j-6)+VTM(i+2,j+6))+
                   +0.25*(VTM(i-2,j)+VTM(i,j+6)+VTM(i,j-6)+VTM(i+2,j))+
                   +0.2*(VTM(i-2,j-3)+VTM(i-1,j-6)+VTM(i-2,j+3)+VTM(i-1,j+6)+
                   +VTM(i+1,j-6)+VTM(i+2,j-3)+VTM(i+2,j+3)+VTM(i+1,j+6)))/7.8
   END DO
END DO

! povprečenje zelene barve
DO j=2,3*W,3
   DO i=1,H
        IT(i,j)=(VTM(i,j)+0.5*(VTM(i,j+3)+VTM(i,j-3)+VTM(i-1,j)+VTM(i+1,j))+
                   +0.375*(VTM(i-1,j-3)+VTM(i+1,j-3)+VTM(i-1,j+3)+VTM(i+1,j+3))+
                   +0.175*(VTM(i-2,j-6)+VTM(i-2,j+6)+VTM(i+2,j-6)+VTM(i+2,j+6))+
                   +0.25*(VTM(i-2,j)+VTM(i,j+6)+VTM(i,j-6)+VTM(i+2,j))+
                   +0.2*(VTM(i-2,j-3)+VTM(i-1,j-6)+VTM(i-2,j+3)+VTM(i-1,j+6)+
                   +VTM(i+1,j-6)+VTM(i+2,j-3)+VTM(i+2,j+3)+VTM(i+1,j+6)))/7.8
   END DO
END DO

! povprečenje modre barve
DO j=3,3*W,3
   DO i=1,H
        IT(i,j)=(VTM(i,j)+0.5*(VTM(i,j+3)+VTM(i,j-3)+VTM(i-1,j)+VTM(i+1,j))+
                   +0.375*(VTM(i-1,j-3)+VTM(i+1,j-3)+VTM(i-1,j+3)+VTM(i+1,j+3))+
                   +0.175*(VTM(i-2,j-6)+VTM(i-2,j+6)+VTM(i+2,j-6)+VTM(i+2,j+6))+
                   +0.25*(VTM(i-2,j)+VTM(i,j+6)+VTM(i,j-6)+VTM(i+2,j))+
                   +0.2*(VTM(i-2,j-3)+VTM(i-1,j-6)+VTM(i-2,j+3)+VTM(i-1,j+6)+
                   +VTM(i+1,j-6)+VTM(i+2,j-3)+VTM(i+2,j+3)+VTM(i+1,j+6)))/7.8
   END DO
END DO

Na podoben način zapišemo še v primeru ostalih dveh filtrov. Na koncu mora uporabnik zapisati še ime izhodne datoteke in podatki se v datoteko nato zapišejo:

       WRITE(*,*) 'Napisi ime izhodne datoteke tipa *.ppm:'
       READ(*,*) IFILE
       OPEN(2,FILE=IFILE,STATUS='NEW')
       WRITE(2,13) TD,'# Created by Tblur',W,H,S
13   FORMAT(A2/A18/I5,I4/I3)
       DO i=1,H
           WRITE(2,14) (IT(i,j),j=1,W)
       END DO
14   FORMAT (2000(I3,1X))
       CLOSE(2)

Če želite lahko program Tblur presnamete na svoj računalnik: tblur.exe
 

4. Zagon programa Tblur in primeri

Zagon:

Program Tblur najprej presnemite v poljuben direktorij na vašem računalniku (npr. C:\DOWNLOAD). Pod isto mapo morate presneti tudi slike grafičnega formata PGM ali PPM, ki jih želite obdelati s programom. Zaženite datoteko oziroma program Tblur.exe in sledite zahtevam programa.
Ker je obdelava rasterskih slik zelo zahtevna, je potrebno upoštevati navodila glede največje velikosti barvne in sivinske slike. Največja velikost barvne slike formata PPM je 1000000 točk, največja velikost sivinske slike formata PGM pa je 3000000 točk.

Priprava slik:

Slike lahko pripravite za obdelavo in si jih nato ogledati s poljubnim grafičnim programom, ki odpira grafična formata PGM in PPM. V okolju MS-Windows priporočam ogled s programom Paint Shop Pro, v okolju X-Windows pa s programom XV.
Program Paint Shop Pro lahko kot shareware dobite zastonj na spletni strani: ftp.arnes.si/software/simtelnet.

Praktična uporaba meglenja slik:

Z zameglitvijo slike dosežemo predvsem zmanjšanje kontrasta med sosednjimi točkami. To pomeni, da zmanjšamo šum v tistih delih slike, kjer prihaja do ostrih barvnih sprememb. Ostri barvni prehodi se zgladijo s povprečenjem barv točk. Šum na sliki ni nič drugega kot zelo visoka frekvenca slike, ki se pojavlja na omejenih področjih. Učinek zameglitve je najbolj izrazit na črnobelem posnetku. Zameglitev se velikokrat uporablja na skeniranih slikah, na katerih vedno nastane sivkast zrnat film. Z zameglitvijo se zrna eliminirajo, toda na žalost se izgubijo ostri robovi predmetov na sliki. Prav zaradi tega z zameglitvijo na smemo preveč pretiravati.
Obstaja boljši način odstranitve tega filma, in sicer s frekvenčnimi operacijami. Če sliko obravnavamo kot kombinacijo različnih frekvenc, jo s Fourier-jevo transformacijo pretvorimo v spekter moči, odstranimo odvečno frekvenco (npr. zrnat film) in na koncu izvedemo še inverzno transformacijo.
Zameglitev slike se velikokrat uporablja tudi pri umetniških slikah, da se dosežejo posebnih efekti. Lahko pa meglenje uporabljamo za navidezno zmanjšanje zrnatosti, predvsem pri črnobelih slikah. Če sliko močno povečamo, bomo zagotovo opazili zrnatost. Z majhno zameglitvijo slike se opazovalcu zazdi, da je zrnatost zmanjšanja. Ostri barvni prehodi se pri tem zgladijo, kar daje željeni učinek. Vendar pa zameglitev v tem primeru ne sme biti prevelika, saj lahko izgubimo ostre robove predmetov, slika pa postane zelo obremenjujoča za oči.
Meglenje slike uporabljamo tudi takrat, kadar želimo poudariti predmete v ospredju. V tem primeru zameglimo ozadje in tako zmanjšamo navidezno globino ter povečamo pozornost na objekte v ospredju.

S programom Tblur lahko sivinsko ali barvno sliko zameglimo na tri načine, kot je prikazano na naslednjih slikah:

Sivinska slika formata PGM:


Slika 6: Osnovna sivinska slika



Slika 7: Zamegljena slika (Blur)



Slika 8: Zamegljena slika (Gaussian blur)



Slika 9: Zamegljena slika (More blur)


Učinek zgladitve ostrih barvnih prehodov s povprečenjem barv točk je najbolj opazen pri črnobeli sliki, kjer sta prisotni le črna in bela barva. Po zameglitvi se na prehodu iz črne na belo barvo pojavijo tudi sivi odtenki:


Slika 14: Osnovna črno-bela slika



Slika 15: Zamegljena slika (More blur)


Barvna slika formata PPM:


Slika 10: Osnovna barvna slika



Slika 11: Zamegljena slika (Blur)



Slika 12: Zamegljena slika (Gaussian blur)



Slika 13: Zamegljena slika (More blur)


Posebni filtri:

Predhodno smo zapisali, da imajo mnogi grafični programi na voljo tudi posebne filtre za zameglitev. Lahko pa filtre v teh programih izdelamo tudi sami. Npr. v programu Paint Shop Pro 5 zaženemo ukaz Image/User Defined Filters.../New... in napišemo vrednosti elementov filtra, ki ga nato uporabimo na izbrani sliki. Tako izdelane filtre lahko poimenujemo in shranimo.

Kot primer lahko navedemo filter, ki zamegli sliko v izbrani smeri (Motion blur). Učinek je podoben, kot bi s fotoaparatom slikali predmet v gibanju. Na spodnji sliki je zanimiva predvsem vodoravna smer, to je smer letenja letala. Da dosežemo željeni učinek, moramo v filtru uteži postaviti v izbrani smeri.

Z ustreznim filtrom ustvarimo učinek gibanja:
0
0
0
0
0
0
0
0
0
0
1
1
1
1
1
0
0
0
0
0
0
0
0
0
0


Slika 15: Osnovna sivinska slika



Slika 16: Zamegljena slika (Motion blur)


Zelo zanimiva je zameglitev slike s poudarkom robov. Učinek dosežemo s filtrom, ki ima v središču matrike negativno vrednost, vrednosti v sosednijh celicah pa so pozitivne in simetrično razporejene:

1
1
1
1
-4
1
1
1
1


Slika 17: Osnovna sivinska slika



Slika 18: Zameglitev s poudarkom robov


 

5. Literatura

1

Howard E.Burdick
Digital imaging
McGraw-Hill, 1997
2

Linnea Dayton and Jack Edition
The Photoshop 3 Wow! Book
McGraw-Hill, 1997

Avtor:

Tomaž Bučar
Zaboršt 58
1262 Dol pri ljubljani
Slovenija
tel:+386 61/788-159
e-mail:tomaz.bucar@kiss.uni-lj.si