Ko je model sestavljen želimo, da bi ga lahko gledali z različnih strani, ga približali ali oddaljili in celo izvedli "prehod skozi" (walk through) ali "prelet okrog" (fly around) modela. Vse to je s PEX-om enostavno izvedljivo.
Spremembe pogledov so proces, s katerim povemo PEX-u kje smo glede na model in kako ga želimo videti. To so interaktivni procesi.
Obstaja več modelov pogledov (viewing models), ki jih s PEX-om lahko uporabljamo. Model pogledov določa veličine, ki so uporabljene za sestavo pogleda. Preprost model pogleda predvideva: polje pogleda (field of view), smer pogleda (viewing direction) in točko gledišča (eye point). Bolj splošen model ima več parametrov in je bolj prilagodljiv. PEXlib določa zelo prilagodljiv model pogledov, ki zadosti potrebam večine aplikacij. S klicanjem dveh uporabnih funkcij kreiramo nizek nivo transformacij pogledov potrebnih PEX-u.
PEXlib predvideva dva modela pogledov, od katerih je eden bolj splošen. Ogledali si bomo bolj splošen model, ki se uporablja tudi v PHIGS-u in drugih 3D vmesnikih.
Določiti moramo vse faktorje, ki vplivajo na sliko:
- kako daleč od modela stojimo in ali vidimo celo sceno
- središče scene, kamor je usmerjena kamera
- pokončen ali vodoraven položaj kamere
To so faktorji, ki jih je dokaj lahko določiti, težje jih je matematično natančno opredeliti z določenimi vrednostmi, ki jih potem posredujemo PEXlib-u. PEXlib določa poti za predstavitev teh veličin, mi se moramo odločiti za njihove vrednosti. Programer mora jasno opredeliti vse vpletene faktorje in ker ti vplivajo drug na drugega, moramo vedeti kako delujejo v celoti.
Ko je stopnja modeliranja končana, imamo določeno sceno v 3D splošnem koordinatnem sisiemu (WC). Vsak objekt je postavljen v določen položaj glede na izhodišče splošnega koordinatnega sistema (WC). Naša naloga je določitev 2D slike te scene na zaslonu.
Najprej izberemo točko, kamor bo usmerjena kamera in s tem določimo smer pogleda. To točko imenujemo referenčna točka pogleda (view reference point), ki lahko leži kjerkoli v splošnem koordinatnem sistemu (WC).
Nadalje izberemo določeno smer, ki naj bo smer skozi referenčno točko pogleda. Položaj kamere določimo nekje na tej liniji. Kje je to nas sedaj še ne zanima. Določiti pa moramo kako je kamera obrnjena oz. katera smer ja za kamero navzgor. Rezultat tega je normalni vektor "usmeritve navzgor". Smer ni nikakor omejena z orientacijo splošnega koordinatnega sistema (WC). Je pa smer navzgor ponavadi pravokotna na smer pogleda.
Z določitvijo referenčne točke pogleda, smeri pogleda in "smer navzgor" za kamero, imamo določen nov koordinatni sistem imenovan referenčni koordinatni sistem pogleda VRC (view reference coordinate system).
Za VRC koordinatni sistem velja:
- izhodišče koordintnega sistema je referenčna
točka pogleda
- smer pogleda je os z koordinatnega sistema VRC
- ploskev x-y je ravnina pravokotna na smer pogleda - os
z in gre skozi referenčno točko pogleda
- "smer navzgor" je os y
- os x je tretja koordinata pravokotna na osi y
in z
Koordinatni sistem VRC v PEXlib-u določa orientacijo pogleda (view orientation). Za poznavanje tega moramo vedeti nekaj več.

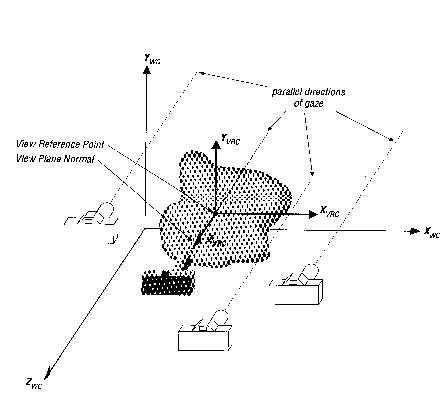
1.) Smer pogleda se imenuje normala pogledne ravnine (view plane normal). Položaj kamere ni omejen samo na lego v tej smeri. Kamero lahko s te linije umaknemo, vendar je vedno usmerjena vzporedno z normalo pogledne ravnine. Glej sliko 15. Povedano drugače, referenčna točka pogleda in normala pogledne ravnine določata neskončno možnih smeri pogleda, ki pa so med seboj vzporedne.
2.) Normala pogledne ravnine je usmerjena linija ali vektor, ki gre od referenčne točke pogleda navzven. Kamera je usmerjena v nasprotni smeri normale pogledne ravnine. Ko določimo normalo pogledne ravnine, ki je os z za naš koordinatni sistem VRC, moramo namestiti kamero na pozitivno stran osi z. To pomeni namestiti kamero "nasproti" sceni. Če želimo iti "za" sceno, moramo določiti normali pogledne ravnine nasprotno smer. Dokler ne določimo smeri normale pogledne ravnine, ne moremo govoriti o tem kaj je "nasproti" in kaj "za". Od naše izbire smeri gledanja je odvisno kaj je "nasproti" in kaj "zadaj".
3.) Čeprav si mislimo, da je "smer navzgor" določena pravokotno na normalo pogledne ravnine, lahko določimo vektor pogleda navzgor (view up vector), ki je usmerjen kamorkoli, le vzporedno z normalo pogledne ravnine ne. PEXlib sam preračuna pravo "smer navzgor" s projekcijo vektorja na ravnino x-y koordinatnega sistema VRC, kjer projekcija postane os y .
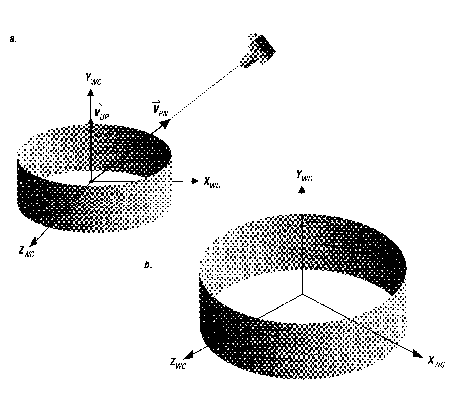
Vzemimo za naš model odprt cilinder s slike 16a. Njegovo središče je v izhodišču splošnega koordinatnega sistema (WC). Dober pogled nanj dobimo, če se postavimo nasproti na desno in rahlo navzgor. Glej sliko 16a. Kamero usmerimo v njegovo središče, torej določimo referenčno točko pogleda (0, 0, 0). Vektor pogleda navzgor določimo (0, 1, 0), kar je vzporedno z osjo y. Smer pogleda pa je vzporedno z vektorjem (1, 1, 1), ki je naša normala pogledne ravnine. Tako orientacijo pogleda prikazuje slika 16a. Rezultat pogleda je na sliki 16b.
Naloga je določiti parametre orientacije pogleda in izračunati transformacijo orientacije pogleda, ki jo pošljemo PEX-u. Primer nastavitve parametrov orientacije pogleda je:
PEXCoord view_ref_pt; PEXVector view_up_vec, view_plane_normal; view_ref_pt.x = 0; view_ref_pt.y = 0; view_ref_pt.z = 0; view_up_vec.x = 0; view_up_vec.y = 1; view_up_vec.z = 0; view_plane_normal.x = 1; view_plane_normal.y = 1; view_plane_normal.z = 1;
Te parametre moramo preurediti s transformacijo orientacije pogleda. To naredimo s funkcijo PEXViewOrientationMatrix:
PEXViewEntry view;
int err;
err = PEXViewOrientationMatrix(
&view_ref_pt,
&view_plane_normal,
&view_up_vec,
view.orientation);
Funkcija vrne transformacijo pogleda vrnjeno v členu view.orientation, ki jo posredujemo PEXlib-u v tabeli pogleda.
Funkcija PEXViewOrientationMatrix je določena:
int PEXViewOrientationMatrix(
PEXCoord *view_ref_pt,
PEXVector *view_plane_normal,
PEXVector *view_up_vec,
PEXMatrix orientation_matrix)
Argumenti so:
view_ref_pt ... kazalec na referenčno točko pogleda
view_plane_normal ... kazalec na vektor normale na pogledno ravnino
view_up_vec ... kazalec na vektor pogleda navzgor
orientation_matrix ... spremenljivka, v kateri PEXlib vrne
preračunano transformacijo orientacije pogleda
Funkcija vrača:
Osnovna orientacija pogleda pomeni:
- referenčna točka pogleda je v izhodišču
splošnega koordinatnega sistema (WC)
- vektor pogled navzgor je v smeri osi y WC
- normala pogledne ravnine je v smeri osi z WC
S temi vrednostmi VRC sovpada s splošnim koordinatnim sistemom WC. Glej sliko 17. Določeno je, da je pozitivna smer osi y v koordinatnem sistemu WC, smer vektorja pogleda navzgor (view_up_vec) in je smer pogleda v nasprotni smeri osi z v WC.
Osnovna orientacija bo delovala pravilno, če postavimo objekt v splošnem koordinatnem sistemu (WC) tako, da je pogled razumen. To pomeni, da mora model ustrezati enotskim meram kocke, ki ima spodnji levi kot v izhodišču splošnega koordinatnega sistema (WC).
Določili smo parametre, ki so potrebni za orientacijo, ne vemo pa: kje v smeri pogleda je postavljena kamera, kako široko in visoko bo kamera zajela sceno, katero pravilo bomo uporabili za spremembo objektov v 3D prostoru v 2D projekcijo in kje v oknu se bo pojavila izbrana podoba. Vse to določimo z načrtovanjem pogleda (view mapping), ki pretvori celo sceno ali le njen določen del v ravno podobo.
Kot primer načrtovanja pogleda poglejmo primer osnovnega (splošnega) načrtovanja pogleda. Ta je določen sledeče:
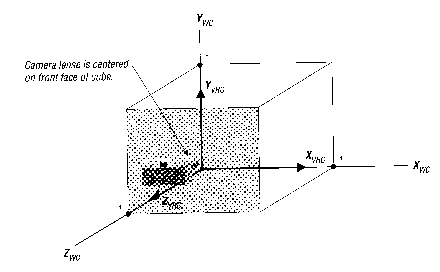
Vidno polje je omejeno na vse kar je znotraj enotske kocke splošnega koordinatnega sistema (WC) od izhodišča v pozitiven oktant. To pomeni, da vidimo samo tisto, kar je znotraj koordinat x, y, z med 0 in 1. Glej sliko 17.
Kamera je postavljena v središče "prednje" strani kocke pri z = 1. Položaj v WC koordinatah je (0.5, 0.5, 1).
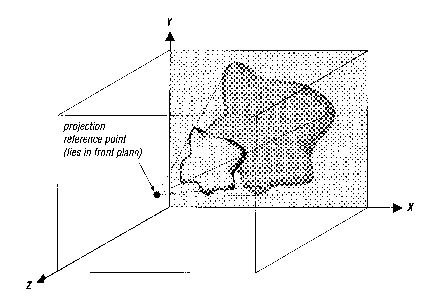
Model projeciramo na "zadnjo" stran kocke, ki leži na ravnini x-y. Tu se nekoliko oddaljimo od podobnosti snemanja s kamero. Namesto projekcije na film kamere si zamislimo kraj, kjer bomo namestili kamero. To je referenčna točka projekcije (projection reference point). S te točke se vse projecira na ravnino x-y. Glej sliko 18. Na zadnjo stran kocke pade le določen del projecirane podobe. Ta je "ujet" za prikaz.
Slika 18 prikazuje, kaj je mišljeno kot projekcija vsebine volumna na ravnino. Če si zamislimo površino objektov znotraj kocke kot zbirko točk in narišemo linijo od referenčne točke projekcije skozi vsako točko površine, lahko določimo kje ta linija preseka ravnino x-y (razen primerov kjer je linija vzporedna ravnini x-y). Te točke na ravnini x-y ustvarijo podobo, ki se imenuje perspektiva projekcije. Osnovno (splošno) načrtovanje uporablja vzporedno projekcijo. Ta se razlikuje od perspektivne projekcije po tem, da je razdalja od zadnje strani kocke do referenčne točke projekcije neskončna (koordinata z je neskončna, x in y koordinati pa sta nespremenjeni), tako da so vse linije perspektive med seboj vzporedne.
Skoraj vse parametre, ki določajo pogled, lahko spremijamo. Videli smo že, da referenčni koordinatni sistem (VRC), ki je določen z orientacijo, ne sovpada nujno s splošnim kordinatnim sistemom (WC). Podobno lahko prosto izbiramo tudi vrednosti pri načrtovanju pogleda.
Opazili smo že lahko, da pri perspektivni projekciji nismo ujeli celotne notranjosti enotske kocke. Projecirali smo le objekte, ki so bili znotraj piramidnega volumna. Vrh te piramide je bil v referenčni točki projekcije, osnovna ploskev pa notranjost na zadnji strani kocke. Glej sliko 18. Drugače pa je pri vzporedni projekciji, kjer "ujamemo" celotno notranjost kocke. Ta prostor, ki je projeciran na 2D projecirno površino, ki obdaja vse primitive, ki jih dejansko vidimo, imenujemo volumen pogleda (view volume). Velikost in obliko tega volumna določa pet faktorjev. Prikazani so na sliki 19.
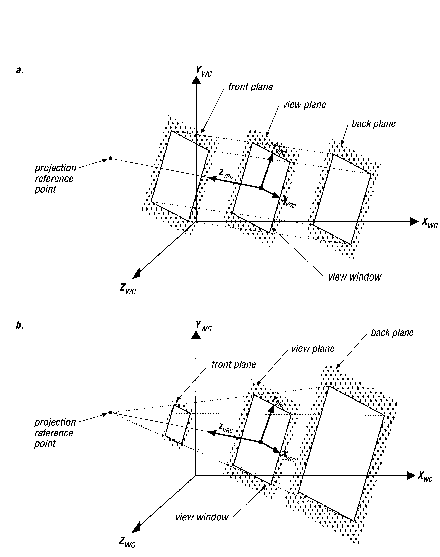
To je lahko katerakoli ploskev vzporedna z ravnino x-y referenčnega koordinatnega sistema (VRC). Kot bomo videli pozneje je nekoliko omejena. Prednja ploskev določa prednjo stran volumna pogleda.
Tudi ta je lahko katerakoli ploskev vzporedna ravnini x-y VRC-ja. Biti mora na isti strani referenčne točke projekcije kot je prednja ploskev in bolj oddaljena od te točke kot je prednja ploskev. Zadnja ploskev označuje zadnjo stran volumna pogleda. Prednja in zadnja ploskev skupaj določata globini volumna pogleda.
Ploskev pogleda je ploskev, na katero je model projeciran. V našem preprostem primeru s slike 17, je ploskev pogleda zadnja stran enotske kocke in je hkrati tudi ravnina x-y VRC-ja. Ploskev pogleda je lahko katerakoli ploskev vzporedna ravnini x-y. Leži lahko celo izven volumna pogleda, za zadnjo ploskvijo ali pred prednjo ploskvijo, vendar za referenčno točko projekcije. Ponavadi ploskev pogleda leži med prednjo in zadnjo ploskvijo ali sovpada z eno od njiju.
Okno pogleda je poseben pravokotnik na ploskvi pogleda. Določa širino in višino volumna pogleda.
V primeru perspektivne projekcije (slika 19b) je referenčna točka projekcije točka, iz katere so vsi objekti projecirani na okno pogleda. V primeru vzporedne projekcije (slika 19a) so linije projeciranja vzporedne liniji, ki teče iz referenčne točke projeciranja v središče okna pogleda. V obeh primerih referenčna točka projekcije ponavadi leži na normali pogledne ravnine (os z VRC). Leži lahko kjerkoli, le med prednjo in zadnjo ploskvijo ali na ploskvi pogleda ne. Lahko si zamislimo premikanje referenčne točke projekcije skozi prostor, medtem pa ostane ploskev pogleda nespremenjena in pravokotna na os z. Namišljeno oko nam pokaže sliko dinamično spremenljive podobe.
Gornji parametri določajo volumen pogleda in samo projecirano podobo. Objekti izven volumna pogleda se navadno ne prikažejo, čeprav lahko spremenimo tudi to.
Vsi parametri za načrtovanje pogleda so podani relativno na koordinatni sistem VRC in ne na splošni koordinatni sistem (WC). Prednja, zadnja in ploskev pogleda so določene z razdaljo vzdolž osi z od referenčne točke pogleda. Okno pogleda je določeno z 2D točkami z koordinatama x in y v koordinatnem sistemu VRC. Koordinate z okna pogleda pa sovpadajo s koordinatami z ploskve pogleda. Referenčna točka projekcije je na osi z koordinatnega sistema VRC in tako sta koordinati x in y nič. Orientacija pogleda ne orientira samo kamere, ampak določa tudi koordinatni sistem in s tem načrtovanje pogleda. Orientacijo moramo torej pametno izbrati. Referenčno točko pogleda ne moremo postaviti v nek popolnoma prost položaj, ampak mora biti usklajen s položajem modela.
Navedeni so primeri določitve parametrov za načrtovanje pogleda:
PEXCoord prp; PEXCoord2D view_window[2]; double view_plane, back_plane, front_plane; int perspective; perspective = True; view_plane = 0; prp.x = 0; prp.y = 0; prp.z = 10; view_window[0].x = -1.5; view_window[1].x = 1.5; view_window[0].y = -1.5; view_window[1].y = 1.5; back_plane = -1.5; front_plane = 1.5;
Podane parametre posredujemo funkciji PEXViewMappingMatrix, ki izvrši transformacijo.
PEXViewEntry view;
int err;
err = PEXViewMappingMatrix(view_window, &viewport,
perspective, &prp, view_plane, back_plane,
front_plane, view.mapping);
Funkcija PEXViewMappingMatrix je določena:
int PEXViewMappingMatrix(
PEXCoord2D view_window[2],
PEXNPCSubVolume *proj_viewport,
int perspective,
PEXCoord *proj_ref_point,
double view_plane,
double back_plane,
double front_plane,
PEXMatrix mapping_matrix)
Argumenti so:
view_window ... polje med dvema točkama okna pogleda. Prva določa levo spodnje ogljišče in druga desno zgornje ogljišče okna.
proj_viewport ... področje v NPC koordinatah, v katero se načrtuje volumen pogleda
perspective ... neke vrste "stikalo" za določitev projekcije. True določa projekcijo v perspektivi, False pa vzporedno projekcijo.
proj_ref_point ... kazalec na referenčno točko projekcije
view_plane ... položaj ploskve pogleda v VRC (koordinata z)
back_plane ... položaj zadnje ploskve v VRC (koordinata z)
front_plane ... položaj prednje ploskve v VRC (koordinata z)
mapping_matrix ... spremenljivka, v katero se zapiše transformacija načrtovanja pogleda
Funkcija vrača:
Parametre funkcije PEXViewMappingMatrix smo že spoznali. Izjema je viewport, ki pa ga bomo opisali kasneje.
Spoznajmo novo dejstvo. Projekcija objekta 3D v podobo 2D se ne izvrši v koordinatnem sistemu VRC. Zgodi se po dodatni transformaciji. Volumen pogleda se najprej prenese v koordinatni sistem, ki je definiran kot 3D kocka, potem pa se izvrši projekcija. Ta koordinaten sistem se imenuje normaliziran projekcijski koordinatni sistem (normalized projection coordinate system NPC).
Za ta zaplet obstajajo trije glavni razlogi:
1.) Splošni koordinatni sistem (WC) je od primera do primera različnih razsežnosti. Določiti moramo, po kakšnih pravilih naj ga prenesemo v okno X, ki je tudi lahko razičnih velikosti. Odgovor je prenos volumna pogleda v nek "združen " predpisan NPC sistem. Temu pa sledi prenos 3D kocke NPC -ja v okno. To loči definicijo pogleda od velikosti okna.
2.) Po določitvi prednje in zadnje strani primitiva, določimo skrite linije in skrite površine. Preračuna pa se vpliv globine prostora (depth cueing). Da se te operacije lahko izvršijo potrebujemo koordinaten sistem orientiran na oko opazovalca, ki bo še vedno razsežnosti 3D. NPC zapolnjuje to potrebo. Os z sistema NPC je vedno usmerjena proti opazovalcu in tako je vse, kar je usmerjeno v pozivni smeri osi z, prednja stran primitiva, kar pa je usmerjeno v negativni smeri osi z, je zadnja stran primitiva.
3.) Ustrezna predstavitev volumna pogleda je potrebna za izvajanje operacije izrezovanja oz. odstranjevanje delov modela, ki jih ne želimo prikazati. Sistem NPC omogoča enostavno označevanje ravnin izsekov.
Pri uporabi vzporedne projekcije se s prenosom volumna pogleda v enotski sistem NPC nič ne spremeni. Zamislimo pa si prenos piramidnega volumna pogleda v sistem NPC. PEX prenese volumen v volumen enotske kocke, ob tem pa se izvrši raztezanje, krčenje ali karkoli drugega. Ta proces je lahko za predstavitev težek, matematično pa ni zahteven in rezultat je primeren.
Določitev smeri navzgor sedaj sovpada z osjo y sistema NPC. Sedaj lahko sploščimo kocko tako, da prikažemo le koordinati x in y vsake točke v tem prostoru in opustimo koordinato z ter tako dobimo 2D projekcijo. Imamo pa še vedno 3D predstavitev podobe in to nam omogoča lažje izrezovanje in izvajanje drugih operacij.
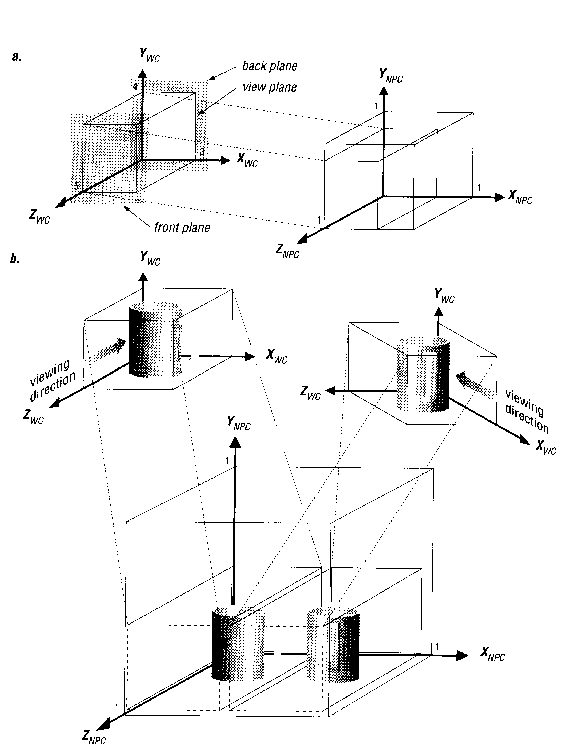
Pri načrtovanju pogleda ni nujno, da volumen pogleda prenesemo v celoten prostor enotske kocke v sistemu NPC. Volumen pogleda lahko prenesemo v katerikoli del te kocke imenovane odprtina pogleda projekcije (projection viewport). Glej sliko 20a.
Nadalje lahko določimo več različnih pogledov in jih prenesemo v različne odprtine pogledov ter s tem razdelimo okno na polja. V vsakem polju prikažemo en pogled. Glej sliko 20b.
Odprtino pogleda projekcije določimo v koordinatah NPC od zadnje spodnje leve točke do prednje zgornje desne točke. Večina programov s knjižnico PEXlib uporablja celotno enotsko kocko, tako da je odprtina omejena s točkama (0, 0, 0) in (1, 1, 1).
PEXNPCSubVolume viewport; viewport.min.x = 0; viewport.max.x = 1; viewport.min.y = 0; viewport.max.y = 1; viewport.min.z = 0; viewport.max.z = 1;
Struktura PEXNPCSubVolume je določena:
typedef struct{
PEXCoord min;
PEXCoord max;
}PEXNPCSubVolume;
Odprtina pogleda se posreduje funkciji PEXViewMappingMatrix, ki vgradi projekcijo odprtine pogleda v vrnjeno matriko transformacije načrtovanja pogleda.
Transformaciji - orientacija pogleda in načrtovanje pogleda ter operaciji - izsek in "stikalo" izseka so glavni deli definicije pogleda (view definition) ali samo view (pogled). Definicija pogleda se shrani v tabelo pogleda (view table) prikazovalnika (renderer-ja). To je ena od tabel stanja (PEX Lookup tables).
Vsak zapis v tabeli ima parametre kot je opisano in je naslovljen z indeksom pogleda (view index). V tabeli pogleda je lahko večje število zapisov. Ponavadi ima tabela v naprej določene zapise, ki jih potem popravljamo, lahko pa tudi kreiramo nove.
Pogled na predmet izberemo z navedbo indeksa pogleda med operacijo obdelave (traversal) strukture s funkcijo PEXSetViewIndex:
void PEXSetViewIndex(
Display *dpy,
XID resource_id,
PEXOCRequestType request_type,
unsigned int view_index)
Nov je argument:
Ta funkcija kreira izhodni ukaz za spremembo veljavnega indeksa pogleda v vodu seznama stanja (pipeline state list). Veljaven indeks določa zapis, ki opiše pogled, ki naj ga PEX uporabi za prikaz primitivov. Osnovni splošni indeks je 0.
V našem primeru smo določili pogled:
unsigned int view_num = 1; PEXSetViewIndex(dpy, model, PEXOCStore, view_num);
Tabelo pogleda nastavimo s funkcijo PEXSetTableEntries:
void PEXSetTableEntries(
Dysplay *dpy,
PEXLookupTable table,
unsigned int start,
unsigned int num_entries,
int table_type,
PEXPointer entries)
Argumenti so:
Pogled je definiran s strukturo:
typedef struct{
unsigned short clip_flag;
unsigned short reserved;
PEXNPCSubVolume clip_limits;
PEXMatrix orientation;
PEXMatrix mapping;
}PEXViewEntry;
Transformacije orientacije pogleda in načrtovanje pogleda sta podani v orientation in mapping članih strukture.
Primer uporabe funkcije PEXSetTableEntries:
unsigned int view_num = 1;
PEXLookupTable view_table;
PEXViewEntry view;
PEXSetTableEntries(dpy, view_table, view_num, 1,
PEXLUTView, (PEXPointer) &view);
V tem primeru funkcija nastavi zapis 1 v tabeli podani z view_table na vrednosti vsebovane v view.
Rekli smo že, da se koordinata z zavrže, dejansko pa se pretvori v koordinate načrta DC (device coordinates) in se opusti potem, ko je že uporabljena za določitev kaj se vidi in kaj ne (skrite linije in površine).
Odprtina pogleda prikazovalnika je izražena v koordinatnem sistemu načrta (DC) in velikost je podana v točkah na zaslonu (pixlih).
Pokazali bomo kako uporabimo orientacijo pogleda za interaktivno spreminjanje kotov pod katerimi gledamo model. To naredimo s spreminjanjem normale na pogledno ravnino kot odziv na premikanje miške. Preprost način za kontrolo normale na pogledno ravnino je kontrola sferičnih koordinat. Glej sliko 21. Vodoraven pomik miške pomeni spremembo kota vektorja okrog osi y (theta) in navpičen pomik miške spremeni kot vektorja okoli ravnine x-z (phi). Tako velja:
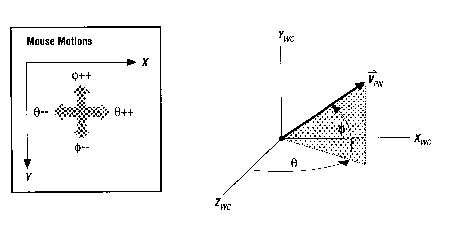
view_plane_normal.x = cos(phi)*sin(theta); view_plane_normal.y = sin(phi); view_plane_normal.z = cos(phi)*cos(theta);
Začetna vrednost za normalo na pogledno ravnino je (1, 1, 1) in ustreza kotoma:
theta = phi = M_PI/4;
Koti se ob vsakem malenkostnem premiku miške spremenijo za faktor:
#define PAN_SCALE (M_PI/500)
in kota sta:
theta += PAN_SCALE*(event.xmotion.x - lastx); phi += PAN_SCALE*(lasty - event.xmotion.y);
lastx in lasty sta spremenljivki, ki povesta položaj miške pred pomikom. Ena točka na zaslonu (pixel) pri spremembi položaja pomeni M_PI/500 spremembe kota v radianih, kot sprememba kota pogleda.
Ko imamo novo normalo na pogledno ravnino, lahko ponovno izračunamo matriko orientacije pogleda in popravimo parametre v tabeli pogleda.
/*Sprememba normale na pogledno ravnino*/
view_plane_normal.x = cos(phi)*sin(theta);
view_plane_normal.y = sin(phi);
view_plane_normal.z = cos(phi)*cos(theta);
/*Izracun transformacije orientacije pogleda*/
err = PEXViewOrientationMatrix(&view_ref_pt, &view_plane_normal,
&view_up_vec, view.orientation);
/*Popravljanje parametrov v tabeli pogleda*/
if(!err){
PEXSetTableEntries(dpy, view_table, view_num, 1,
PEXLUTView, (PEXPointer) &view);
lastx = event.xmotion.x;
lasty = event.xmotion.y;
redraw();
}
Pomembno je, da preverimo vrnjeno vrednost funkcije PEXViewOrientationMatrix, ker parametri orientacije lahko postanejo nepravilni (normala na pogledno ravnino lahko postane vzporedna na vektor view_up_vec). V tem primeru ne vnesemo novih podatkov v tabelo pogleda.