S pomočjo računske geometrije se rešujejo tudi problemi,
ki nastajajo pri načrtovanju delovnih gibov robotov. Na prvi pogled
izgledajo algoritmi precej abstraktni, brez večjih povezav z realnim
stanjem, vendar se izkažejo za učinkovite pri proučevanju dejanskih
razmer.
Robot oziroma delovna roka robota R je premikajoči se objekt,
ki ima specifične geometrijske karakteristike. Lahko ga opišemo
kot točko, linijski segment, konveksni mnogokotnik, itd. Robot
R je v nekem začetnem položaju s. Naloga je oblikovati
načrt gibanja tako, da pride R do končnega položaja, ne
da bi pri tem trčil v katerokoli oviro. Zdrs meje R ob
mejo ovire ni trk. Tako določeno pot se imenuje prosta pot. Pri
tem nastanejo trije bistveni problemi:
1. Ali obstaja prosta pot za R od s do t.
2. Poiskati prosto pot za R od s do t.
3. Poiskati najkrajšo prosto pot za R od s
do t.
Pojem 'najkrajša' ni vedno popolnoma jasen. Predvsem ne v primerih,
ko je R linijski segment in je dovoljeno njegovo vrtenje.
Najkrajša pot obstaja, če sploh obstaja kakšna pot med s
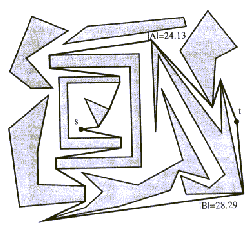
in t. Na Sliki 7.1 je prikazan primer, kjer je s
začetna točka, t pa končna. Ovire so prikazane kot mnogokotniki
na ravnini. Za s in t velja, da nista v notranjosti
nobenega teh mnogokotnikov. Vrisani sta dve izmed možnih poti.
Pot A in pot B. Pot A je krajša in je sploh
najkrajša možna pot danega primera.

Navadno je prvi korak določitev vseh možnih poti in hkrati določitev
ožjega izbora, v katerem je gotovo tudi najkrajša pot. V ta ožji
izbor sodijo tiste poti, katerih segmenti imajo krajišče v s
in t in v temenih mnogokotnikov (ovir). Točki s
in t sta tako lahko upooštevani kot mnogokotnika z enim
samim temenom. Ožji izbor je t.i. vidnostni graf. Vidnostni graf
niza mnogokotnikov je graf, katerega vozlišča sovpadajo s temeni
mnogokotnikov, njegovi robovi pa povezujejo ta vozlišča tako,
da nobeno ne pade v notranjost kateregakoli mnogokotnika (ovire).
Vidnostni graf Slike 7.1 je prikazan na Sliki 7.2.
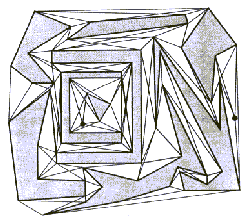
S konstrukcijo vidnostnega grafa je določen ožji izbor, to je
končen niz poti od s do t, med katerimi je tudi
najkrajša mogoča pot. Naslednji korak je torej iz ožjega izbora
določiti najkrajšo pot. Dolžina je preprosto določena z vsoto
dolžin vseh linijskih segmentov, ki pot določajo. Algoritem za
določanje najkrajše poti temelji na enakomernem oddaljevanju od
začetne točke s po vseh možnih poteh. Ko je po določenem
času dosežena končna točka t, je ob poznavanju hitrosti
oddaljevanja določljiva najkrajša pot.
Naj bo R konveksen mnogokotnik, ki predstavlja roko robota,
naj bo rR osnovna točka. Naj bo P ovira. Potem je
P'=P-R niz točk, ki je za r prepovedan
v smislu, da:
1. Če se R premakne tako, da je točka r nedvoumno v notranjosti P', potem R
zadane v P.
2. Če se R pomika tako, da r leži na P', potem se R dotika P.
3. Če se R pomika tako, da je r nedvoumno
zunaj P', potem je RP=.
V nadaljevanju je v grobem predstavljen algoritem za določevanje poti konveksnega mnogokotnika R.
Naj bodo P1,P2,...,Pm ovire na poti s skupnim
številom temen n. Algoritem je sestavljen iz štirih korakov:
1. Povečanje vseh ovir na Pi'=Pi-R.
2. Določiti unijo P'=iPi'.
3. Poiskati del, kjer sta točki s in t.
4. Poiskati pot med točkama s in t v tem
delu.
Na Sliki 7.3 je prikazana roka robota R in osem ovir (pobarvane
temno). Prostor, kjer je mogoče gibanje, je sestavljeno iz treh
delov. V njih so točke a,b in c. Iz začetnega
stanja, kot je prikazano na sliki, R lahko doseže le točko
a, točki b in c sta nedosegljivi. Tako je
vprašanje, ali je t dosegljiv iz s, zreducirano
na, ali sta točki s in t v istem delu.
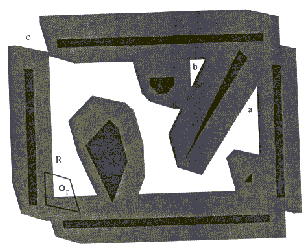
Slika 7.3 Robot - konveksni mnogokotnik R z osnovno
točko r. Konveksni mnogokotniki (pobarvani temno) predstavljajo
ovire na poti R, senčeno področje je P', kamor osnovna
točka r ne sme prodreti po zgoraj omenjenih treh pravilih.
Podpodročje načrtovanja gibanja je načrtovanje gibanja veččlenkaste
roke robota. To je veriga linijskih elementov Li, i=1,...,n,
ki so med seboj povezani v členkih Ji, i=1,...,n.
Členek J0 je pritrjen na temelj. Členek Ji za 0in
je členek med Li in Li+1. Jn je vrh Ln
(Slika 7.4).
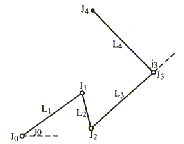
Dolžina elementa Li je li in je načeloma nespremenljiva. Kot z vrhom v Ji je ji, merjen v nasprotni smeri urinih kazalcev med Li in Li+1. Kot je merjen od pozitivne osi x. Roka A je določena s seznamom dolžin elementov Li: (l1,...,ln). Niz točk, ki je dosegljiv z veččlenkasto roko, je vedno zaprt med dva koncentrična kroga, ki imata središče v J0 in polmera ri in r0.
Naj bo A=(l1,l2) roka z dvema členkoma. Če
je l1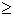 l2, je dosegljivo področje
kolobar z zunanjim radijem r0=l1+l2 in notranjim
radijem ri=l1-l2 (Slika 7.5a). Če je l1=l2
je ri=0. Če je l1l2 (Slika 7.5b), je dosegljivo
področje še vedno kolobar z r0=l1+l2 in r=l2-l1
ali ri=l1-l2.
l2, je dosegljivo področje
kolobar z zunanjim radijem r0=l1+l2 in notranjim
radijem ri=l1-l2 (Slika 7.5a). Če je l1=l2
je ri=0. Če je l1l2 (Slika 7.5b), je dosegljivo
področje še vedno kolobar z r0=l1+l2 in r=l2-l1
ali ri=l1-l2.
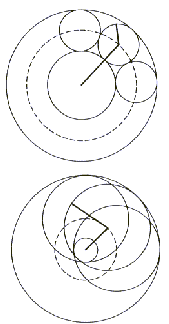
Razporeditev elementov Li glede na njihove dolžine li
ni pomembno, saj razporeditev ne vpliva na dosegljivost (Slika
7.6).
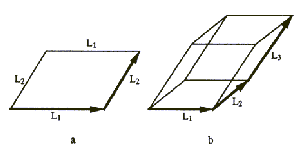
Slika 7.6 Paralelogram za dva (a) in tri (b) linijske segmente
kažeta, da vrstni red ne vpliva na dosegljivost.
Zunanji polmer je tako vedno 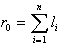 . Za notranji
radij ni vedno tako preprosto. Da je ri0, mora biti najdaljši
segment roke daljši, kot so skupaj dolgi vsi ostali segmenti.
To je najbolje vidno, če je najdaljši segment prvi v nizu A
(Slika 7.8).
. Za notranji
radij ni vedno tako preprosto. Da je ri0, mora biti najdaljši
segment roke daljši, kot so skupaj dolgi vsi ostali segmenti.
To je najbolje vidno, če je najdaljši segment prvi v nizu A
(Slika 7.8).
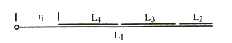
Sledi torej, da je dosegljivo področje centrični kolobar z zunanjim
premerom 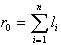 in notranjim ri=0, če
je najdaljiši segment dolžime lM
krajši kot polovica celotne dolžine roke, drugače je
in notranjim ri=0, če
je najdaljiši segment dolžime lM
krajši kot polovica celotne dolžine roke, drugače je 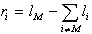 .
.
V to področje spadajo še razni primeri ločljivosti.