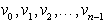 točke na ravnini, naj bodo
točke na ravnini, naj bodo 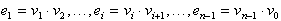 linijski segmenti, ki povezujejo točke na ravnini med seboj. Obojih
je n in določajo mnogokotnik, če:
linijski segmenti, ki povezujejo točke na ravnini med seboj. Obojih
je n in določajo mnogokotnik, če:
V računski geometriji imajo velik pomen mnogokotniki.
Z njimi se lahko popisujejo objekti v realnem svetu, hkrati pa
so primerni za računalniško obdelavo. Po zgradbi so lahko povsem
enostavni, tak je s tremi linijskimi elementi trikotnik, lahko
pa so sestavljeni iz več tisoč elementov. Večje, kompleksnejše
mnogokotnike je ponavadi potrebno razstaviti na več enostavnejših
delov.
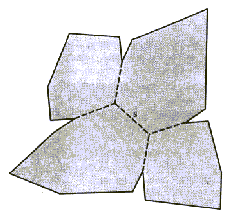
Definicija mnogokotnika: Mnogokotnik je območje na ravnini,
ki je od okolice razmejeno z nizom linijskih elementov. Topološko
gledano je mnogokotnik homeomorfična oblika kroga, oziroma njegova
deformacija.
Naj bodo 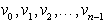 točke na ravnini, naj bodo
točke na ravnini, naj bodo 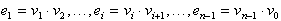 linijski segmenti, ki povezujejo točke na ravnini med seboj. Obojih
je n in določajo mnogokotnik, če:
linijski segmenti, ki povezujejo točke na ravnini med seboj. Obojih
je n in določajo mnogokotnik, če:
1. Je presečišče med dvema sosednjima linijskima segmentoma,
v krožnem redu, ena sama skupna točka: 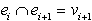 ,
za vse
,
za vse  .
.
2. Se nesosednji segmenti ne sekajo med seboj: 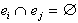 ,
za vse
,
za vse 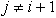 .
.
Prvi pogoj daje mnogokotniku podobnost krogu zaradi krožnega stikanja
linijskih segmentov med seboj po sistemu konec z začetkom. Drugi
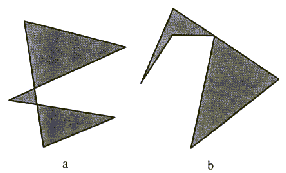
pogoj pa definira enostavnost mnogokotnikov. Poznamo tudi neenostavne
mnogoktnike (Slika 2.1).
Točke na ravnini vi so temena mnogokotnika, linijske povezave
med njimi ei so robovi mnogokotnika. Vsak enostaven mnogokotnik
P razdeli ravnino na dva dela. Meja mnogokotnika P
je 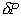 . Velja
. Velja 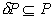 .
.
Pri manipuliranju z mnogokotniki je potrebno te večkrat deliti na manjše, enostavnejše dele. Osnovna delitev je triangulacija oziroma delitev na trikotnike. Pri tem se postavlja vprašanje, ali se lahko preko vsakega mnogokotnika izvede triangulacijo.
Obstoj triangulacije je tesno povezan z obstojem diagonale v mnogokotniku,
to pa se lahko postavi le, če ima mnogokotnik vsaj eno nedvoumno
izbočeno teme. Iz tega se lahko postavijo trije logični zaključki:
1. Vsak mnogokotnik mora imeti najmanj eno nedvoumno izbočeno teme.
2. Vsak mnogokotnik z 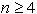 temeni ima
diagonalo.
temeni ima
diagonalo.
3. Vsak mnogokotnik 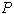 z
z 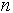 temeni se da razdeliti na trikotnike (triangulirati) z dodajanjem
(nobene ali večih) diagonal.
temeni se da razdeliti na trikotnike (triangulirati) z dodajanjem
(nobene ali večih) diagonal.
Za dokaz prve postavke je potrebno privzeti mejo P mnogokotnika
P kot pot, po kateri hodi hodec v nasprotni smeri urinih
kazalcev. Vsak njegov obrat v levo označuje nedvoumno izbočeno
teme, vsak njegov obrat v desno pa nedvoumno vbočeno teme. Naj
bo L premica, ki teče skozi najnižje teme mnogokotnika
v; najnižje glede na koordinato y. Če je takih temen
več, naj bo to najbolj desno, najnižje teme. Notranjost mnogokotnika
P je nad premico L. V temenu v hodec nedvoumno
naredi obrat v levo, kar pomeni, da ima vsak mnogokotnik najmanj
eno nedvoumno izbočeno teme (Slika 2.2).
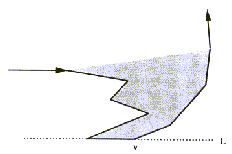
Slika 2.2 V nejbolj desnem, najnižjem temenu se hodec obrne
v levo; teme v je nedvoumno izbočeno.
Naj bosta temeni pred in za temenom v označeni z a
in b. Če daljica ab meje P ne seka, niti
se je ne dotika, potem je ab nedvoumno diagonala. Če pa
ab seka oziroma se dotika meje P, potem ima ta mnogokotnik
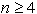 , trikotnik avb pa vsebuje še najmanj
eno teme mnogokotnika P, ki ni a, v ali b.
Naj bo x teme mnogokotnika P v trikotniku avb,
ki je najbližje temenu v v pravokotni smeri na ab.
Tako je teme x prvo teme, ki ga zadane premica L,
ko se pomika iz temena v proti ab. Nedvoumno v prostoru
avb, ki je omejen s polravnino L (temno senčeno
na sliki), ni nobene točke meje P, razen temena x.
Tako je daljica vx nedvoumno diagonala mnogokotnika P
(Slika 2.3).
, trikotnik avb pa vsebuje še najmanj
eno teme mnogokotnika P, ki ni a, v ali b.
Naj bo x teme mnogokotnika P v trikotniku avb,
ki je najbližje temenu v v pravokotni smeri na ab.
Tako je teme x prvo teme, ki ga zadane premica L,
ko se pomika iz temena v proti ab. Nedvoumno v prostoru
avb, ki je omejen s polravnino L (temno senčeno
na sliki), ni nobene točke meje P, razen temena x.
Tako je daljica vx nedvoumno diagonala mnogokotnika P
(Slika 2.3).

Dokaz o obstoju diagonale posredno dokazuje, da se da vsak mnogokotnik
razdeliti na trikotnike. Naj bo 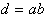 diagonala
mnogokotnika P. Po definiciji diagonala d seka mejo
mnogokotnika
diagonala
mnogokotnika P. Po definiciji diagonala d seka mejo
mnogokotnika 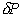 samo v svojih krajiščih.
Diagonala d razdeli mnogokotnik P na dva mnogokotnika
P', ki imata manj kot n temen, in s tem postane
del
samo v svojih krajiščih.
Diagonala d razdeli mnogokotnik P na dva mnogokotnika
P', ki imata manj kot n temen, in s tem postane
del 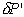 . V vsakem mnogokotniku P'
je mogoče določiti novo diagonalo
. V vsakem mnogokotniku P'
je mogoče določiti novo diagonalo 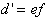 , ki
P' razdeli na dva manjša mnogokotnika (Slika 2.4). Ta proces
se lahko ponavlja, dokler mnogokotnik P ni razdeljen na
same trikotnike.
, ki
P' razdeli na dva manjša mnogokotnika (Slika 2.4). Ta proces
se lahko ponavlja, dokler mnogokotnik P ni razdeljen na
same trikotnike.

Triangulacijo preko mnogokotnika je mogoče narediti na več načinov,
število katerih narašča z n. Za vse velja, da je za triangulacijo
mnogokotnika P potrebno 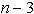 diagonal,
ki mnogokotnik P razdelijo na
diagonal,
ki mnogokotnik P razdelijo na 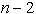 trikotnikov. Vsota vseh notranjih kotov mnogokotnika P
z n temeni je
trikotnikov. Vsota vseh notranjih kotov mnogokotnika P
z n temeni je 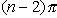 .
.
V teoriji grafov ima pomembno mesto t.i. dualnost grafa. Gre za
lastnost, da je določene podatke moč predstaviti na več načinov
(dva-dual). Triangulacija mnogokotnika P je ponavadi predstavljena
z vrisanimi diagonalami, lahko pa tudi z grafom T, ki je
druga oblika predstavitve istih podatkov. Graf T, dualnost
triangulacije mnogokotnika je graf, ki je sestavljen iz vozlišč
in povezav med njimi. Vozlišča predstavljajo trikotnike triangulacije,
povezave med njimi pa skupne stranice trikotnikov triangulacije
oziroma digonalo, ki je skupna dvema trikotnikoma (Slika 2.5).
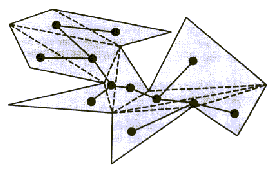
Velja, da je graf T, dualnost triangulacije, drevo, ki
je sestavljen iz vozlišč, v katerih se srečajo največ tri povezave.
Vozlišča grafa T stopnje ena so končne točke grafa T
oziroma uhlji mnogokotnika P. Vozlišča druge stopnje ležijo
na veji T in jo podaljšujejo. Vozlišča tretje stopnje so
razvejišča grafa T. Iz povedanega sledi, da ima vsak mnogokotnik
z 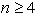 temeni vsaj dva neprekrivajoča se uhlja.
temeni vsaj dva neprekrivajoča se uhlja.
Razdeljevanje na trikotnike se uporablja pri preračunavanju površine
mnogokotnikov. Mnogokotnik se razdeli na trikotnike, izračuna
se površino posameznega trikotnika, vsota površin vseh trikotnikov
je površina mnogokotnika.
V splošnem je površina trikotnika osnovnica krat višina polovic.
Vendar v pogojih, ko so podana temena a,b,c
trikotnika T na ravnini, ta formulacija ni več primerna.
V tem primeru je uporaben vektorski produkt, katerega velikost
predstavlja površino paralelograma s stranicama A in B.
Polovica paralelograma je trikotnik s stranicama A in B,
pri čemer velja 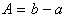 in
in 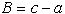 .
Vektorski produkt je izračunljiv s pomočjo determinante:
.
Vektorski produkt je izračunljiv s pomočjo determinante:
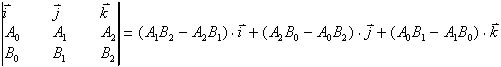
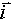 ,
, 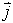 in
in 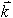 so enotski vektorji v x, y in z smeri. V
dvodimenzijskem prostoru sta
so enotski vektorji v x, y in z smeri. V
dvodimenzijskem prostoru sta 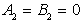 , od zgornjega
izraza ostane
, od zgornjega
izraza ostane 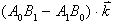 . Površina trikotnika, če
se upošteva
. Površina trikotnika, če
se upošteva 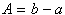 in
in 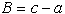 ,
je:
,
je:
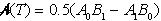 ,
,
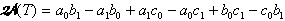 .
.
V deterministični obliki je dvakratna površina trikotnika 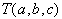 izračunljiva z:
izračunljiva z:
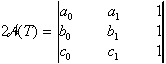 .
.
Vsak konveksen mnogokotnik se lahko trivialno razdeli na trikotnike
tako, da se eno krajišče vseh diagonal d pripne v eno teme
vk (Slika 2.6).
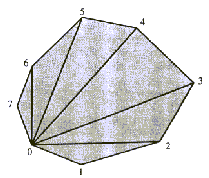
Slika 2.6 Tiangulacija konveksnega mnogokotnika; vse diagonale
imajo eno skupno krajišče v temenu v0.
Površina tako razdeljenega mnogokotnika, ki ima temena
označena v nasprotni smeri urinih kazalcev z 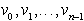 ,
je lahko zapisana kot
,
je lahko zapisana kot
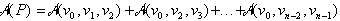 .
.
Ker je razdeljevanje na trikotnike izvedljivo na več načinov,
je tudi površino mnogokotnika moč zapisati na več načinov. Naj
bo 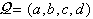 štiristrani konveksen mnogokotnik,
ki ga je mogoče razdeliti na trikotnike na dva načina (Slika 2.7).
štiristrani konveksen mnogokotnik,
ki ga je mogoče razdeliti na trikotnike na dva načina (Slika 2.7).
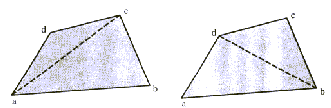
V prvem primeru velja:
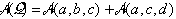
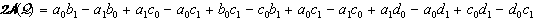 ,
,
po ureditvi
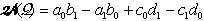 .
.
Do enakega izraza se pride tudi v drugem primeru. Razvidno je,
da izraz ne vsebuje segmenta ac, kar pomeni, da postavitev
diagonale ne vpliva na končni rezultat 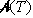 .
.
Če so temena štiristranega konveksnega mnogokotnika popisana s koordinatama xi in yi, je splošna enačba za izračun dvojne površine mnogokotnika enaka
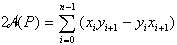 .
.
Pri nekonveksnem štiristranem mnogokotniku (Slika 2.8) je možen
en sam način triangulacije. Diagonala ac je izven mnogokotnika,
ostane le ena notranja diagonala ab. Površina mnogokotnika
je:
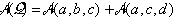 .
.
Zaradi lastnosti vektorskega produkta je površina acd negativna
in se od abc odšteje. Tako prej omenjena enačba za izračun
površine štiristranih konveksnih mnogokotnikov velja tudi za štiristrane
nekonveksne mnogokotnike.

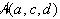 je negativna.
je negativna.
Izkaže se, da je enačba za izračun površine štiristranih mnogokotnikov
splošna in velja tudi za mnogokotnike, katerih 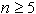 .
.
Pri posplošitvi omenjenega načina, pri katerem se seštevajo površine
trikotnikov, naj bo izhodišče točka p, ki je povsem poljubna
in naj leži zunaj mnogokotnika P (ni nujno). Naj bo 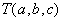 trikotnik, katerega temena so orientirana v nasprotni smeri urinih
kazalcev, naj bo p katerakoli točka na ravnini. Potem velja:
trikotnik, katerega temena so orientirana v nasprotni smeri urinih
kazalcev, naj bo p katerakoli točka na ravnini. Potem velja:
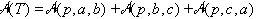 .
.

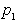 in
in 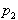 .
.
Naj bo izhodiščna točka 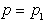 (Slika 2.9).
Potem je prvi člen enačbe za izračun površine
(Slika 2.9).
Potem je prvi člen enačbe za izračun površine 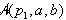 negativen zaradi svoje orientiranosti; ostala dva člena sta pozitivna.
Površina
negativen zaradi svoje orientiranosti; ostala dva člena sta pozitivna.
Površina 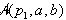 predstavlja natančno tisto površino
štiristranega mnogokotnika
predstavlja natančno tisto površino
štiristranega mnogokotnika 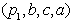 , ki je zunaj
trikotnika T. Tako je končna površina natančno kot določena
, ki je zunaj
trikotnika T. Tako je končna površina natančno kot določena
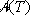 . Podobno velja tudi za izhodiščno točko
. Podobno velja tudi za izhodiščno točko
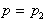 . Obe površini,
. Obe površini, 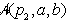 in
in 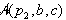 sta zaradi svoje orientiranosti negativni
in se od
sta zaradi svoje orientiranosti negativni
in se od 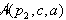 , ki je pozitivna, odštejeta.
Ostanek je natančno
, ki je pozitivna, odštejeta.
Ostanek je natančno 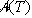 . Podobno velja za
katerokoli poljubno točko na ravnini, znotaj ali zunaj trikotnika
T.
. Podobno velja za
katerokoli poljubno točko na ravnini, znotaj ali zunaj trikotnika
T.
Pri razdeljevanju mnogokotnikov na trikotnike je najprej potrebno
poiskati diagonalo mnogokotnika. Diagonala razdeli mnogokotnik
na dva dela. Postopek je potrebno ponavljati, dokler mnogokotnik
ni razdeljen na same trikotnike. Da je daljica 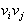 ,
,
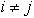 diagonala mnogokotnika P mora
veljati: da ne seka meje mnogokotnika P in, da je v vsej
svoji dolžini v notranjosti P. Diagonale mnogokotnika
se med seboj ne sekajo.
diagonala mnogokotnika P mora
veljati: da ne seka meje mnogokotnika P in, da je v vsej
svoji dolžini v notranjosti P. Diagonale mnogokotnika
se med seboj ne sekajo.
Določanje diagonal je preprosta aplikacija, ki se ponavlja, dokler
niso določene vse diagonale mnogokotnika: za vsak rob e mnogokotnika
P, ki ne seka nobenega konca diagonale s, se preveri,
če e seka s. Ko je ugotovljeno presečišče med e
in s, daljica s ni diagonala mnogokotnika. Če noben
tak rob ne seka s, potem je s diagonala mnogokotnika
P. V primeru kolinearnosti točk ta način ni uspešen (Slika
2.10).

Če je rob, sosedenj robu i, kolinearen z ij, potem
ij ni diagonala. Naj bo 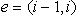 rob mnogokotnika,
kolinearen z ij. Mogoča sta primera, ko je daljica ij
daljša od e; pri
rob mnogokotnika,
kolinearen z ij. Mogoča sta primera, ko je daljica ij
daljša od e; pri 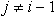 (Slika 2.10a)
in ko je daljica ij krajša od e (Slika 2.10b), vendar
ta ni več enostaven mnogokotnik.
(Slika 2.10a)
in ko je daljica ij krajša od e (Slika 2.10b), vendar
ta ni več enostaven mnogokotnik.
Vzporedno z aplikacijo določanja diagonal je potrebno za vsako
diagonalo preveriti, če ne seka druge diagonale. To se preveri
z medsebojnim primerjanjem koordinat krajišč obeh diagonal. Na
koncu je potrebno za vsko diagonalo preveriti, če leži v notranjosti
mnogokotnika P (Slika 2.11).

Vprašanje notranjosti in zunanjosti je test lokalne narave. Če
je diagonala 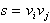 v okolici obeh temen
v okolici obeh temen 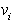 in
in 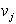 v notranjosti mnogokotnika P,
potem je v notranjosti mnogokotnika v vsej svoji dolžini. Diagonala
v vsej svoji dolžini namreč ne seka meje mnogokotnika P.
Zadostno je testiranje ene same končne točke diagonale. Če je
diagonala s v okolici točke vi v notranjosti mnogokotnika,
potem je v notranjosti mnogokotnika tudi v okolici točke vj
in obratno. Podobno velja tudi za zunanjost. Test se tako zoži
na pregled okolice točke vi. Možna sta primera, ko je vi
izbočeno (Slika 2.12a) ali vbočeno (Slika 2.12b) teme.
v notranjosti mnogokotnika P,
potem je v notranjosti mnogokotnika v vsej svoji dolžini. Diagonala
v vsej svoji dolžini namreč ne seka meje mnogokotnika P.
Zadostno je testiranje ene same končne točke diagonale. Če je
diagonala s v okolici točke vi v notranjosti mnogokotnika,
potem je v notranjosti mnogokotnika tudi v okolici točke vj
in obratno. Podobno velja tudi za zunanjost. Test se tako zoži
na pregled okolice točke vi. Možna sta primera, ko je vi
izbočeno (Slika 2.12a) ali vbočeno (Slika 2.12b) teme.

Slika 2.12 Diagonala 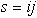 je v trikotniku
določenim z
je v trikotniku
določenim z 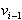 ,
, 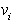 ,
,
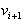 : (a) izbočeno;(b) vbočeno.
: (a) izbočeno;(b) vbočeno.
Na sliki 2.12a je diagonala ij s krajiščem v izbočenem
temenu v. Jasno je, da je diagonala v notranjosti mnogokotnika
P, če je v notranjosti trikotnika z vrhom v temenu v.
To pomeni, da mora biti teme 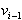 na levi
strani
na levi
strani 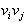 in teme
in teme 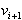 ne levi strani
ne levi strani 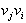 . Ta pogoj se preverja
s pomočjo računanja površine med točkami i, j in
i-1 ter med točkami i, i+1 in j. Če
je površina pozitivna, potem predpostavka levega drži, če je negativna,
predpostavka levega ne drži.
. Ta pogoj se preverja
s pomočjo računanja površine med točkami i, j in
i-1 ter med točkami i, i+1 in j. Če
je površina pozitivna, potem predpostavka levega drži, če je negativna,
predpostavka levega ne drži.
V primeru vbočenosti temena i ta način odpove, saj sta
lahko temeni i-1 in i+1 hkrati obe na desni, obe
na levi ali vsako na svoji strani diagonale ij. Podobnost
s prejšnjim primerom je ta, da je notranjost pri izbočenem temenu
enaka zunanjosti pri vbočenem temenu. Notrajnost in zunanjost
sta zamenjani. Pri drugem primeru torej velja (test po istem načinu
kot pri izbočenem temenu), če diagonala ni zunanja, potem je notranja.
Testira se zunanjost. Pred testiranjem notranjosti oziroma zunanjosti
je tako potrebno določiti, ali je vi izbočeno ali vbočeno
teme. Teme vi je izbočeno, če je teme 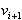 na levi strani ali na
na levi strani ali na 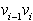 . Po dogovoru je
teme
. Po dogovoru je
teme 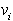 , pri katerem je notranji kot enak
, tudi izbočeno.
, pri katerem je notranji kot enak
, tudi izbočeno.
Zgoraj omenjeni način razdeljevanja mnogokotnikov na trikotnike
se ne uporablja prav pogosto, saj je zaradi svoje strukture vsakokratnega
pregeledovanja pravilnosti diagonale precej počasen.
Hitrejši je način, pri katerem se postavlja diagonalo med temeni
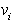 in
in 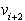 , pri čemer
mora biti
, pri čemer
mora biti 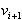 izbočeno teme. Ta način se
imenuje tudi način odrezovanja uhljev mnogokotnika. Po definiciji
ima vsak mnogokotnik z
izbočeno teme. Ta način se
imenuje tudi način odrezovanja uhljev mnogokotnika. Po definiciji
ima vsak mnogokotnik z 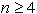 vsaj dva neprekrivajoča
se uhlja. Na sliki 2.13 je
vsaj dva neprekrivajoča
se uhlja. Na sliki 2.13 je 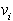 ,
, 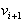 ,
,
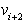 uhelj mnogokotnika.
uhelj mnogokotnika.
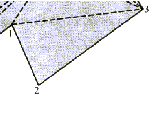
Triangulacija se začne v izhodiščnem temenu 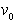 .
Poiskati je potrebno prvo trojico temen
.
Poiskati je potrebno prvo trojico temen 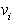 ,
,
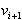 ,
, 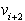 , ki določajo
uhelj mnogokotnika, t.j. izbočeno teme z vrhom v temenu
, ki določajo
uhelj mnogokotnika, t.j. izbočeno teme z vrhom v temenu 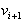 .
Ko je taka trojica najdena, je daljica
.
Ko je taka trojica najdena, je daljica 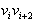 diagonala mnogkotnika. Trikotnik
diagonala mnogkotnika. Trikotnik 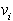 ,
, 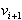 ,
,
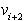 se odreže od preostanka mnogokotnika.
Postopek se ponavlja, dokler od mnogokotnika ne ostane samo (zadnji)
trikotnik. Triangulacija po načinu odrezovanja uhljev je s tem
končana (Slika 2.14). Izhoden podatek je seznam diagonal, ki so
definirane z lastnimi krajišči glede na označevanje vhodnega podatka
mnogokotnika (Tabela 2.1).
se odreže od preostanka mnogokotnika.
Postopek se ponavlja, dokler od mnogokotnika ne ostane samo (zadnji)
trikotnik. Triangulacija po načinu odrezovanja uhljev je s tem
končana (Slika 2.14). Izhoden podatek je seznam diagonal, ki so
definirane z lastnimi krajišči glede na označevanje vhodnega podatka
mnogokotnika (Tabela 2.1).
Tabela 2.1: Izhodni podatek, seznam diagonal za sliko 2.14.
| Diagonale: | |
| 1 - 3 | 12 - 14 |
| 4 - 6 | 9 - 14 |
| 3 - 6 | 8 - 14 |
| 3 - 7 | 8 - 15 |
| 1 - 7 | 7 - 15 |
| 0 - 7 | 7 - 16 |
| 9 - 11 | 7 - 17 |
| 9 - 12 |
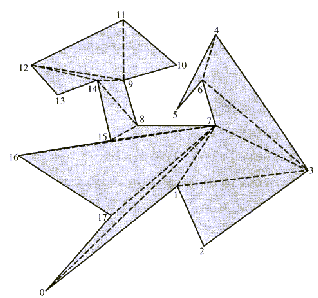
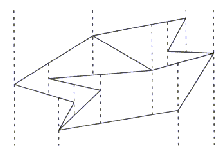
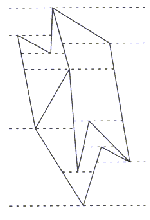
Poleg razdeljevanja na trikotnike, je mnogokotnik moč razdeliti
tudi na trapeze; na konveksne površinske elemente. Ta razdelitev
je lahko osnova za nadaljno razdeljevanje na trikotnike. Razlika
med triangulacijo in razdeljevanjem na trapeze je ta, da so pri
prvi razdelitveni elementi diagonale, pri drugi pa horizontalne
oziroma verikalne (horizontalna in vertikalna razdelitev na trapeze)
linije skozi temena v, ki so v primeru mnogokotnika omejene
z mejo mnogokotnika P (Slika 2.15), v primeru ureditve
linijskih elementov pa s temi elementi ali pa se nadaljujejo v
neskončnost (Slika 2.16).
Razdeljevanje na trapeze je lahko izvedeno z različnimi algoritmi.
Z determinističnimi ali z naključnimi inkrementalnimi algoritmi.
Pri determinističnem načinu gre za pregledovanje mnogokotnika
oziroma planarnega grafa s pomočjo horizontalne ali vertikalne
linije. Če se privzame za pregledovalno linijo vertikalo, potem
koordinata x predstavlja čas, v katerem se linija L
pomika od 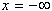 proti
proti 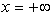 .
Naj bo N niz n linearnih segmentov na ravnini (Slika
2.16).
.
Naj bo N niz n linearnih segmentov na ravnini (Slika
2.16).
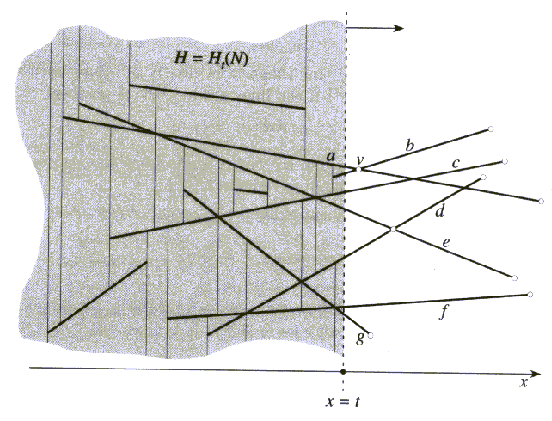
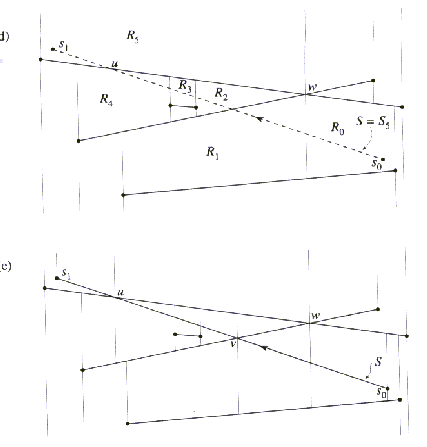
Naj bo H(N) trapezoidna dekompozicija, ki jo želimo dobiti
kot izhoden podatek. Naj bo 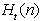 presek med
polravnino
presek med
polravnino 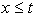 in H(N). Med procesom
pregledovanja je potrebno ohranjati oziroma obnavljati
in H(N). Med procesom
pregledovanja je potrebno ohranjati oziroma obnavljati 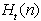 ,
ki pri
,
ki pri 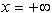 postane H(N).
postane H(N). 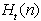 se obnavlja vsakič, ko linija L preide kakšno izmed karakterističnih
točk (krajišče segmenta, presečišče segmentov). Linija L
tako napredujej proti
se obnavlja vsakič, ko linija L preide kakšno izmed karakterističnih
točk (krajišče segmenta, presečišče segmentov). Linija L
tako napredujej proti 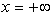 od ene karakteristične
točke do druge. V vsakem trenutku je potrebno vedeti, katera bo
naslednja karakteristična točka, ki jo bo linija L zadela.
Vse karakteristične točke so popisane v t.i. popisu dogodkov.
Razvrščene so po naraščujoči koordinati x. Tako je v vsakem
trenutku
od ene karakteristične
točke do druge. V vsakem trenutku je potrebno vedeti, katera bo
naslednja karakteristična točka, ki jo bo linija L zadela.
Vse karakteristične točke so popisane v t.i. popisu dogodkov.
Razvrščene so po naraščujoči koordinati x. Tako je v vsakem
trenutku 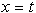 znano, katera karakteristična
točka je prva na desni strani linije
znano, katera karakteristična
točka je prva na desni strani linije 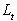 .
Presečišč segmentov v prvi fazi v tem seznamu ni. Ta so določljiva
s pomočjo mejnega seznama. V tem seznamu so zapisani vsi segmenti,
ki jih v danem trenutku
.
Presečišč segmentov v prvi fazi v tem seznamu ni. Ta so določljiva
s pomočjo mejnega seznama. V tem seznamu so zapisani vsi segmenti,
ki jih v danem trenutku 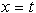 linija L
seka. Za sliko 2.16 je mejni seznam a,b,c,d,e,f,g
Do presečišča lahko pride le med segmentoma, ki sta si v mejnem
seznamu sosednja. Glede na to (Slika 2.16), da se razdalja med
a in b, ko se L približuje presečišču v,
manjša, se lahko vsako naslednje presečišče natančno določi v
naprej. Ko je določeno, se ga pripiše v popis dogodkov. Na začetku
pregledovanja sta H(N) in mejni seznam prazna. V popisu
dogodkov so krajišča vseh elementov N razvrščena po naraščujoči
koordinati x. Vsakič. ko linija L preide karakteristično
točko, se ta v popisu dogodkov zbriše. To pomeni, da se zbriše
točka z najmanjšo vrednostjo x. Ko linija L preide
karakteristično točko p, se dogaja naslednje (Slika 2.17):
linija L
seka. Za sliko 2.16 je mejni seznam a,b,c,d,e,f,g
Do presečišča lahko pride le med segmentoma, ki sta si v mejnem
seznamu sosednja. Glede na to (Slika 2.16), da se razdalja med
a in b, ko se L približuje presečišču v,
manjša, se lahko vsako naslednje presečišče natančno določi v
naprej. Ko je določeno, se ga pripiše v popis dogodkov. Na začetku
pregledovanja sta H(N) in mejni seznam prazna. V popisu
dogodkov so krajišča vseh elementov N razvrščena po naraščujoči
koordinati x. Vsakič. ko linija L preide karakteristično
točko, se ta v popisu dogodkov zbriše. To pomeni, da se zbriše
točka z najmanjšo vrednostjo x. Ko linija L preide
karakteristično točko p, se dogaja naslednje (Slika 2.17):
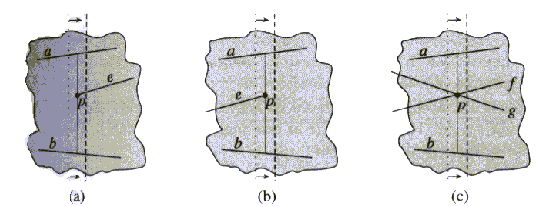
Slika 2.17 Pregledovanje (a) leve krajiščne točke; (b)
desne krajiščne točke; (c) presečišča.
1. Točka p je levo krajišče segmenta 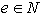 .
V tem primeru se e doda mejnemu seznamu. Segmenta a
in b, za katera se predpostavi, da vedno obstajata (lahko
se ju umetno doda nad in pod vse ostale segmente niza N),
sta pred in za e v popravljenem mejnem seznamu. V tem trenutku
se spremeni tudi H, ki se mu doda segment e in vertikalna
povezava med a in b, ki gre skozi točko p.
V mejnem seznamu sta sedaj segmenta a in e sosednja.
Če se sekata na desni strani točke p, je to presečišče
natančno določljivo. Ob predpostavki, da ga v popisu dogodkov
še ni, se novo presečišče tja vpiše. Isto se naredi tudi za segmenta
b in e.
.
V tem primeru se e doda mejnemu seznamu. Segmenta a
in b, za katera se predpostavi, da vedno obstajata (lahko
se ju umetno doda nad in pod vse ostale segmente niza N),
sta pred in za e v popravljenem mejnem seznamu. V tem trenutku
se spremeni tudi H, ki se mu doda segment e in vertikalna
povezava med a in b, ki gre skozi točko p.
V mejnem seznamu sta sedaj segmenta a in e sosednja.
Če se sekata na desni strani točke p, je to presečišče
natančno določljivo. Ob predpostavki, da ga v popisu dogodkov
še ni, se novo presečišče tja vpiše. Isto se naredi tudi za segmenta
b in e.
2. Točka p je desno krajišče segmenta 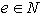 .
V tem primeru se e izbriše iz mejnega seznama. V H
se doda vertikalna povezava med a in b, ki gre skozi
točko p. Segmenta a in b postaneta v popravljenem
mejnem seznamu sosednja. Če se sekata ne desni strani točke p,
je to presečišče natančno določljivo. Ob predpostavki, da ga v
popisu dogodkov še ni, se novo presečišče tja vpiše.
.
V tem primeru se e izbriše iz mejnega seznama. V H
se doda vertikalna povezava med a in b, ki gre skozi
točko p. Segmenta a in b postaneta v popravljenem
mejnem seznamu sosednja. Če se sekata ne desni strani točke p,
je to presečišče natančno določljivo. Ob predpostavki, da ga v
popisu dogodkov še ni, se novo presečišče tja vpiše.
3. Točka p je presečišče dveh segmentov 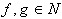 .
V popravljenem mejnem seznamu segmenta f in g zamenjata
mesti. Popravi se H, kamor se vpiše presečišče p
in vertikalna linija med segmentoma a in b, ki gre
skozi točko p. V popravljenem mejnem seznamu sta sedaj
sosednja segmenta a in f ter b in g.
Za oba para je potrebno preveriti mogoče presečišče desno od točke
p (kot opisano v točki 1.) in ob predpostavki, da ga v
popisu dogodkov še ni, se novo presečišče tja vpiše.
.
V popravljenem mejnem seznamu segmenta f in g zamenjata
mesti. Popravi se H, kamor se vpiše presečišče p
in vertikalna linija med segmentoma a in b, ki gre
skozi točko p. V popravljenem mejnem seznamu sta sedaj
sosednja segmenta a in f ter b in g.
Za oba para je potrebno preveriti mogoče presečišče desno od točke
p (kot opisano v točki 1.) in ob predpostavki, da ga v
popisu dogodkov še ni, se novo presečišče tja vpiše.
Inkrementalni algoritem za razdeljevanje na trapeze temelji na
dodajanju linijskih segmentov v niz N po naključnem vrstnem
redu. Za vsak novo dodan linijski segment se doda karakteristične
vertikale, ki so del trapezoidne dekompozicije. Naj bo N
niz n linijskih segmentov na ravnini in H(N)
rezultirajoča trapezoidna dekompozicija. H(N) nastaja
inkrementalno z dodajanjem segmentov iz niza N, enega za
drugim po naključnem vrstnem redu. V i-tem koraku algoritma
je zgrajen 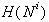 , pri čemer
, pri čemer 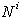 predstavlja niz prvih i-tih naključno izbranih linijskih
segmentov (Slika 2.18 c).
predstavlja niz prvih i-tih naključno izbranih linijskih
segmentov (Slika 2.18 c).
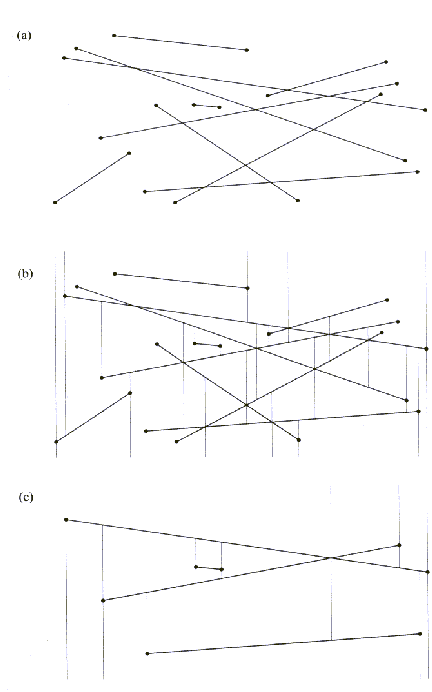
Slika 2.18 (a) N: niz segmentov; (b) H(N);
(c) 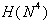 ; (d) potovanje vzdolž
; (d) potovanje vzdolž 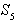 v
v 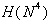 ; (e)
; (e) 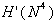 .
.
Predpostavimo, da je določen trapez v 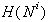 ,
ki vsebuje eno izmed krajišč linijskega segmenta S, naj
bo to točka
,
ki vsebuje eno izmed krajišč linijskega segmenta S, naj
bo to točka 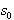 . Potrebno je potovati v
. Potrebno je potovati v 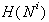 vzdolž linijskega segmenta S od krajišča
vzdolž linijskega segmenta S od krajišča 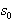 proti krajišču
proti krajišču 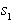 in pri tem pregledovati
že določene trapeze
in pri tem pregledovati
že določene trapeze 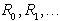 v
v 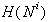 (Slika 2.18d). Naj bo f katerikoli trapez v
(Slika 2.18d). Naj bo f katerikoli trapez v 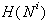 ,
ki ga linijski segment S seka. Vsak tak trapez je potrebno
razdeliti (Slika 2.19) in dodati vertikalo.
,
ki ga linijski segment S seka. Vsak tak trapez je potrebno
razdeliti (Slika 2.19) in dodati vertikalo.
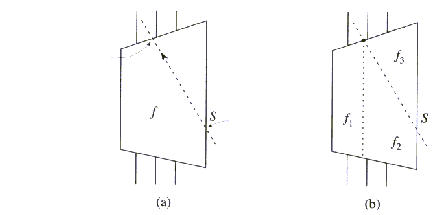
Če linijski segment S preseka zgornjo ali spodnjo stranico
trapeza f, potem je potrebno skozi to presečišče postaviti
vertikalo, ki je sestavni del trapezne dekompozicije. Če krajišče
segmenta S leži v notranjosti trapeza f, kot v primeru
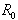 in
in 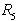 na sliki
2.18d, potem je potrebno skozi to krajišče postaviti vertikalo.
Ko so pregledani vsi trapezi vzdolž segmenta S in dodane
vse vertikale, je določena nova razvrstitev
na sliki
2.18d, potem je potrebno skozi to krajišče postaviti vertikalo.
Ko so pregledani vsi trapezi vzdolž segmenta S in dodane
vse vertikale, je določena nova razvrstitev 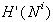 .
Prikazana je na sliki 2.18e. Sledi dodajanje naslednjega linijskega
segmenta iz niza N. Končno stanje je prikazano na sliki
2.18b.
.
Prikazana je na sliki 2.18e. Sledi dodajanje naslednjega linijskega
segmenta iz niza N. Končno stanje je prikazano na sliki
2.18b.
Poleg razdeljevanja na trikotnike in trapeze, je mnogokotnik moč
razdeliti tudi na konveksne površinske elemente. Pri tem se je
potrebno držati dveh načel:
1. Razdeliti mnogokotnik na čim manj konveksnih površinskih elementov.
2. Izvesti to razdelitev v čim krajšem člasu.
Ti dve načeli si nasprotujeta. Tako se možne rešitve razdeljevanja razlikujejo po tem, katero od obeh načel je upoštevano v večji meri. Poiskati je potrebno kompromisno rešitev med obema načeloma.
Dekompozicijo mnogkotnika P je mogoče narediti s pomočjo
diagonale ali s pomočjo segmentov. Razlika je v tem, da so krajišča
diagonal vedno temena 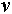 mnogokotnika P,
za segmente pa je pomembno samo to, da njihova krajišča ležijo
nekje na P. Delitev s pomočjo segmentov je precej bolj
zapletena, vendar ponuja optimalnejše rezultate. Teorem (Chazzele)
pravi:
mnogokotnika P,
za segmente pa je pomembno samo to, da njihova krajišča ležijo
nekje na P. Delitev s pomočjo segmentov je precej bolj
zapletena, vendar ponuja optimalnejše rezultate. Teorem (Chazzele)
pravi:
Naj bo najmanjše število konveksnih površinskih elementov. Za
mnogkotnik z r vbočenimi temeni velja, 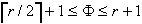 .
.
Če se skozi temena, ki imajo notranji kot (vbočeno), potegne
diagonala, nujno nastaneta dva konveksna površinska elementa.
Število takih elementov je r+1. Z eno diagonalo je torej
mogoče dobiti največ dva taka elementa. Rezultat je 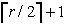 konveksnih elementov (Slika 2.20, Slika 2.21).
konveksnih elementov (Slika 2.20, Slika 2.21).
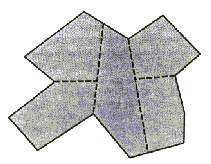
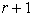 konveksnih
elementov:
konveksnih
elementov: 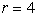 ; 5 elementov.
; 5 elementov.

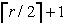 konveksnih
elementov:
konveksnih
elementov: 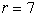 ; 5 elementov.
; 5 elementov.Tako dekompozicijo je mogoče dobiti na način odvzemanja nepomembnih diagonal. Diagonala d je nepomembna za teme v, če bi njena odstranitev ustvarila površinski element, ki bi bil v temenu v vbočen. Teme v mora biti tako v vsakem primeru vbočeno. Vsako vbočeno teme ima največ dve pomembni diagonali. Diagonalo, ki ni pomembna za nobeno teme, imenujemo nepomembna digonala.
Algoritem je preprost. Najprej se preko mnogokotnika P
izvede triangulacija. Nato se po vrsti odvzemajo nepomembne diagonale.
Na sliki 2.22 je prikazano vbočeno teme 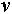 .
Sosednji temeni sta
.
Sosednji temeni sta 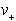 in
in 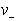 .
Levo od
.
Levo od 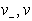 je polravnina
je polravnina 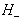 ,
desno od
,
desno od 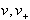 je polravnina
je polravnina 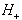 .
Na polravnini
.
Na polravnini 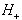 je lahko največ eno pomembna
diagonala. Če sta diagonali dve, je tista, ki je bližja
je lahko največ eno pomembna
diagonala. Če sta diagonali dve, je tista, ki je bližja 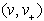 ,
nepomembna. Njena odstranitev v temenu v ne povzroči vbočenosti
površinskega elementa. Podobno velja tudi za polravnino
,
nepomembna. Njena odstranitev v temenu v ne povzroči vbočenosti
površinskega elementa. Podobno velja tudi za polravnino 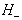 .
.
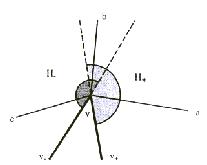
Slika 2.22 Pomembne diagonale. Diagonala a je ne
nepomembna, saj diagonala b v polravnini 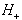 še vedno zagotavlja vbočenost v temenu v. Podobno je tudi
d nepomembna diagonala.
še vedno zagotavlja vbočenost v temenu v. Podobno je tudi
d nepomembna diagonala.
Razdeljevanje s segmenti je precej bolj zapleteno, vendar ponuja
optimalnejše rezultate. Mogoča je tudi delitev, pri kateri se
delitveni segmenti s meje mnogokotnika P ne dotikajo
(Slika 2.23).