UNIVERZA V LJUBLJANI
Fakulteta za strojništvo
REKONSTRUKCIJA POVRŠIN
DIPLOMSKA NALOGA VISOKOŠOLSKEGA ŠTUDIJA
Aleš DROLC
Mentor: izr. prof. dr. Jože Duhovnik, dipl. inž.
Ljubljana, 1997
To diplomsko nalogo posveèam mojim staršem, ki so mi študij omogoèili in mi ves èas stali ob strani.
D Tek. štev.: 4747 UDK 519.68
REKONSTRUKCIJA POVRŠIN
Aleš Drolc
Kljuène besede: Raèunska geometrija, raèunalniška grafika, rekonstrukcija površin, zajem prostorskih toèk, Delaunayeva triangulacija, Voronoi diagram, konveksna lupina, nekonveksna lupina.
Izvleèek: Diplomska naloga predstavlja mehanski sistem za zajem prostorskih toèk in metodo za rekonstrukcijo površine iz razpršenih podatkov. V prvem delu so predstavljene teoretiène osnove raèunske geometrije in osnovni algoritmi, v drugem pa mehanski sistem za zajem prostorskih toèk, z opisom povezave z raèunalnikom, in lgoritem za rekonstrukcijo površine, ki ni nujno konveksna.
D Tek. štev.: 4747 UDC 519.68
SURFACE RECONSTRUCTION
Aleš Drolc
Key words: Computational geometry, computer graphics, surface reconstruction, canning of 3D points, Delaunay triangulation, Voronoi diagram, convex hull, nonconvex hull.
Abstract: In the thesis a mechanical system for scanning 3D points and a method for surface reconstruction from scattered data are presented. In the first part theoretical rounds of computational geometry and some ground applications are described. In the second part a mechanical system for scannin 3D points with description of connection between the system and the computer and the application for surface reconstruction, which is not necessary convex, are presented.
Kazalo
1 Uvod 15
2 Geometrija in osnove algoritmov 25
2.1 Zgodovinska prièakovanja 25
2.1.1 Kompleksnost v klasièni geometriji 25
2.2 Algoritem 25
2.2.1 Algoritem: Izraz in ovrednotenje uèinka 26
2.2.2 Podatkovne strukture 28
2.2.2.1 Podatkovna struktura DCEL 29
2.2.2.2 Odsekova drevesna struktura 30
2.3 Definicije osnovnih geometrijskih elementov 31
3 Mnogokotniki 33
3.1 Definicija mnogokotnika 33
3.2 Triangulacija - razdeljevanje na trikotnike 34
3.2.1 Obstoj izboèenega temena 34
3.2.2 Obstoj diagonale 35
3.2.3 Obstoj triangulacije in njene lastnosti 35
3.2.4 Dualnost triangulacije 36
3.3 Površina mnogokotnika 37
3.3.1 Vektorski produkt 37
3.3.2 Površina konveksnega mnogokotnika 37
3.3.3 Površina štiristranega konveksnega mnogokotnika 38
3.3.4 Površina štiristranega nekonveksnega mnogokotnika 39
3.3.5 Površina mogokotnika, raèunana iz poljubnega centra 40
3.4 Izvedba triangulacije 40
3.4.1 Diagonala - notranja ali zunanja 40
3.4.2 Triangulacija z odstranjevanjem ušes 42
3.5 Razdeljevanje na trapeze 43
3.5.1 Trapezna dekompozicija s pregledovanjem ravnine 44
3.5.2 Inkrementalni algoritem trapezne dekompozicije 46
3.6 Razdeljevanje mnogokotnikov na konveksne površinske elemente 49
3.6.1 Optimalna konveksna razdelitev mnogokotnika 51
3.7 Ravninski elementi v prostoru 51
4 Konveksne lupine v 2D 53
4.1 Algoritem za konstrukcijo lupine v 2D 54
4.1.1 Deterministièen algoritem za konstrukcijo konveksne lupine v 2D 54
4.1.2 Nakljuèni algoritem za konstrukcijo konveksne lupine v 2D 56
4.2 Nekonveksna lupina niza toèk na ravnini 59
5 Konveksne lupine v 3D 61
5.1 Polieder 51
5.2 Inkrementalni algoritem za konstrukcijo konveksne lupine v 3D 64
5.3 Višje dimenzije 66
5.4 Nekonveksna lupina niza toèk v prostoru 68
6 Voronoi diagram 69
6.1 Definicija Voronoi diagrama 69
6.2.1 Odnos med Delaunayevo triangulacijo in Voronoi diagramom 72
6.3 Konstrukcija Voronoi diagrama 73
6.3.1 Deterministièen algoritem za konstrukcijo Voronoi diagrama 73
6.3.2 Inkrementalni algoritem za konstrukcijo Voronoi diagrama 75
6.4 Aplikacije povezane z Voronoi diagrami 76
6.4.1 Najbližji sosed 76
6.4.2 Maksimiziranje najmanjših kotov triangulacije 76
6.4.3 Najveèji prazen krog 77
6.4.4 Najmanjše razvejišèe 79
6.4.5 Problem trgovskega potnika 79
6.5 Posplošitve Voronoi diagrama 79
7 Zajem prostorskih toèk 81
7.1 Mehanski sistem za zajemanje prostorskih toèk 81
7.1.1 Napake pri zajemanju prostorskih toèk 82
7.2 Napajalnik 84
7.3 Analogno digitalni konverter 84
7.3.1 Povezava A/D konverterja z raèunalnikom 84
7.3.2 Komunikacija med raèunalnikom in A/D konverterjem 85
7.4 Doloèanje koordinatnih vrednosti iz geometrije sistema 89
7.5 Zapis zajetih prostorskih toèk v datoteko 90
8 Rekonstrukcija površin 93
8.1 Triangulacija površine 93
8.2 Delaunayeva triangulacija v 2D 94
8.2.1 Najveèji prazen krog 94
8.2.2 Pregledovanje ravnine 96
8.2.3 Princip tretje toèke 96
8.2.3.1 Raèunanje polmera najveèje prazne toèke 97
8.3 Delaunayeva triangulacija v 3D 97
8.4 Proces rekonstrukcije površine - Delaunayeva triangulacija 97
8.4.1 Podatkovne strukture 98
8.4.2 Algoritem rekonstrukcije površine 98
8.4.3 Zaèetek pregledovanja v prostoru 100
8.4.4 Princip tretje toèke 100
8.4.4.1 Postavljanje lokalnega koordinatnega sistema 101
8.4.5 Raèunanje normale 103
8.5 Vhod in izhod 103
8.5.1 Vhod 103
8.5.2 Izhod 104
8.6 Rekonstrukcija površine 106
8.6.1 Oblika in število toèk 106
8.6.2 Primer in uporaba 107
8.7 Problemi 110
9 Zakljuèek 111
Literatura 113
Dodatek 115
1 Uvod
Pri prouèevanju razliènih dogodkov, pojavov, lastnosti elementov, ipd., si je velikokrat pot do rezultata mogoèe olajšati s pomoèjo razliènih analiz ali rekonstrukcij. Podatke, ki jih je mogoèe zbrati na razliène naèine, je potrebno po doloèenih zakonih ali predpisih urediti. Podatki so lahko:
· temperature, izmerjene s temperaturnim senzorjem na razliènih mestih,
· temperature, izmerjene s temperaturnim senzorjem na istem mestu v èasovnih presledkih,
· izmerjeni ekonomskosocialni kazalci,
· izmerjeni pretoki skozi cevovode,
· toèke, doloèene z odèitavanjem površine, itd [9].
Za vse zgoraj naštete podatke (in tudi ostale neomenjene) velja, da so le redko zbrani v neko urejeno obliko, ki bi že sama po sebi ponujala rešitev, ampak jih je potrebno v urejeno obliko šele spraviti. To velja tudi za podatke, ki se jih dobi z odč
itavanjem površine. Ti podatki so ponavadi neurejeni in razpršeni.Podatki, na podlagi katerih je potrebno narediti rekonstrukcijo ploskve, so lahko dobljeni na razliène naèine: z mehanskim sistemom za odèitavanje 3D toèk, z laserskim 3D skenerjem, s pomoèjo ultrazvoka, itd. Te toèke so lahko razpršene po ravnini (2D ali ravninske), ali pa so razpršene v prostoru (3D ali prostorske).
Namen je torej, da bi bilo iz vhodnih neurejenih podatkov, ki so lahko ravninski ali prostorski, mogoèe sklepati o geometriji in topologiji površine, oz. z naèrtnim odèitavanjem toèk zagotoviti digitaliziran model površine ali modela, ki bi ga bilo mogoèe uporabiti pri analiziranju ali pri modeliranju veèjih, bolj zahtevnih oblik. Pri tem je ena možnost naèin, pri katerem se ugotavljajo odnosi med podatki, rezultat pa je popis površine s funkcijo (v odvisnosti od kompleksnosti površine) in drugi, ki temelji na razliènih algoritmih raèunske geometrije, in toèke v prostoru povezuje v "dobre" trikotnik
e, te pa naprej v optimalno trikotniško mrežo.
V nadaljevanju je pozornost posveèena drugi možnosti, t.j. z uporabo razliènih algoritmov raèunske geometrije izdelati algoritem, ki bo sposoben rekonstrukcije površine, ki ne bo nujno konveksna.
Za pridobivanje razpršenih podatkov je bil izbran mehanski sistem za odèitavanje 3D toèk. Pri tem naèinu odèitavanja je najveèji problem natanènost sistema. Za opisan primer je bilo odloèeno, da je poudarek na prikazu postopka odèitavanja in ne na natanènosti sistema. Sistem je sestavljen iz treh palic in treh potenciometrov v treh vrtišèih. Potenciometri odèitavajo relativni kot med posameznimi palicami, kar zadošèa za doloèitev koordinat toèke v prostoru. Z uporabo optiènih enkoderjev v zgibih in po naroèilu izdelanih elementov, bi se natanènost bistveno poveèala, vendar bi se s tem sistem podražil.
V raèunski geometriji vsa teorija temelji na konveksnosti. Tako na stopnji lupin na ravnini, kot tudi kasneje pri konstruiranju lupin v prostoru. Veèina algoritmov, ki gotovo rešujejo probleme pri nedvoumni konveksnosti, pri konstrukciji ali rekonstrukciji površine, ki ni nujno konveksna, v popolnosti odpove. Tako je bilo potre
bno za rešitev združiti različne naèine reševanja in ideje, ki jih uporabljajo razlièni algoritmi, pri tem pa postaviti tudi nekaj omejitev, ki jih na tej stopnji ni mogoèe preseèi.
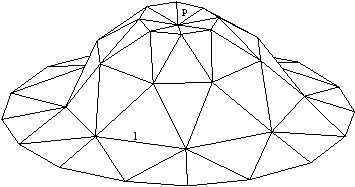
Algoritmi za doloèanje konveksnih lupin temeljijo na ovijanju (deterministièen naèin) ali na dodajanju posameznih toèk in doloèanju, ali leži toèka znotraj ali zunaj lupine in v odvisnosti od tega popravljanju lupine (nakljuèen naèin). Ta dva naèina konkavnosti ne prepoznavata; vsako konkavno teme postavita v notranjost lupine. Na Sliki 1.1 je prikazano konkavno podroèje površine. Zgoraj omenjena naèina toèke p ne bi prepoznala kot del lupin, ampak bi jo postavila v njeno notranjost. Konkavna so tudi vsa temena na robu l. Algoritem, ki bo sposoben prepoznavanja konkavnosti, bo v principu podoben naèinu ovijanja, vendar bo hkrati upošteval odnose med toèkami, kar popisujeta Voronoi diagram in Delaunayeva triangulacija.

Slika 1.1 Konkavno podroèje površine je v toèki p in po robu l.
Lupino je potrebno glede na toèke v prostoru oblikovati iz površinskih elemetnov. To so lahko trikotniki, štirikotniki ali kakšni drugi konveksni mnogokotniki. V nadaljevanju je prikazan postopek, ki lupino v prostoru oblikuje iz optimalnih trikotnikov. Tako razdelitev omogoèa Delaunayeva triangulacija, ki zagotovi maksimiziranje najmanjših kotov (Slika 1.1).
V naslednjem poglavju je predstavljenih nekaj pogledov, ki so v zgodovini vodili, da se je geometrija kot taka sploh rodila in se kasneje pod razliènimi vplivi razvijala do nivoja, na kakršnem je danes. Z uveljavitvijo raèunalnikov se je v sklopu geometrije razvila nova veja, t.i. raèunska geometrija, ki si pri reševanju geometrijskih problemov pomaga s posebnimi podatkovnimi strukturami in z razliènimi metodami reševanja (algoritmi) s pomoèjo raèunalnika.
Splošno gledano je raèunska geometrija prouèevanje algoritmov, s pomoèjo katerih se rešujejo geometrijski problemi na raèunalniku.
Pri ožjem pojmovanju rač
unske geometrije je ta opredeljena kot proces iskanja in razvršèanja preko doloèene množice elementov. Najpreprostejši primer je razvršèanje enodimenzionalnih toèk po koordinatnih vrednostih. Naj bo niz N sestavljen iz n elementov na realni osi R. Pri tem naj R predstavlja enodimenzionalen prostor R1. Naloga je razvrstiti elemente po njihovih koordinatah. Temu ustreza (Slika 1.2):
Problem razvršèanja:
Potrebno je poiskati ureditev H(N) na R, ki bo oblikovana iz danega niza toèk N in bo zadostila zahtevanim pogojem [7].
![]()
Slika 1.2 Razvrstitev H(N) predstavlja ureditev toèk p
i glede na koordinatno vrednost.
S problemom razvršèanja se povezuje problem iskanja.
Problem iskanja:
Potrebno je združiti ureditev
H'(N) z ureditvijo H(N) tako, da je pri katerikoli dani toèki qÎ R mogoèe doloèiti interval v H(N), ki to toèko vsebuje.
V primeru prostorske triangulacije je ureditev H(N) triangualcija T(N) preko danega niza toèk v R3. Ureditev T(N) enaka D(N), t.j. Delaunayevi triangulaciji, ki je najboljša možna razdelitev, saj maksimizira najmanjše kote trikotnikov (Slika 1.3).
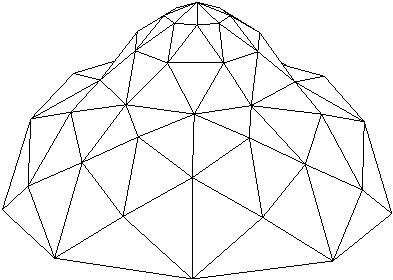
Slika 1.3 D(N); n = 51 niza N v R
3.
Pri dinamiènih procesih se niz N spreminja z dodajanjem oziroma odvzemanjem toèk oz. katerihkoli drugih elementov. Tu je potrebno hitro prilagajanje ureditev H(N) in H'(N) med vsakim dejanjem dodajanja ali odvzemanja.
Problema razvršèanja in iskanja se lahko združita: dan je niz N, sestavljen iz n elementov na osi R. Oblikovati je mogoèe ureditvi H(N) in H'(N). S pomoèjo slednje je mogoèe doloèiti
položaj katerekoli točke v H(N).
Razvršèanje toèk na osi R je najpreprostejši primer raèunske geometrje. Pri premiku v višje dimenzije, niz elementov N ni veè niz toèk, temveè niz linijskih segmentov, ploskev, polprostorov, itd., v R
d prostoru.R
d predstavlja d-dimenzionalen prostor. Razvrstitev H(N) tako predstavlja ureditev vsega ali samo del prostora Rd, v katerem je niz N. H(N) se imenuje tudi geometrijski kompleks. Pod tem se razume zbir razèlenjenih nizov, razliènih dimenzij, skupaj z medsebojnimi povezavami v prostoru Rd. Najpreprostejši primer je planarni graf, ki je sestavljen iz temen, robov in ploskev ter povezav med njimi. Element, v geometrijskem kompleksu, dimenzije j se imenuje j-ploskev. 0-ploskev ali nièdimenzionalna ploskev je teme, 1-ploskev ali enodimenzionalna ploskev je rob, itd. V tem primeru je terminologija prilagojena planarnemu grafu.
Vsakega geometrijskega problema se je mogoèe lotiti s pomoèjo deterministiènih ali nakljuènih algoritmov [7].
Deterministièni naèini:
· Inkrementalna metoda: Dodajanje elementov doloèenega niza enega za drugim po znanem vrstnem redu.
· Deljenje in združevanje: Delitev niza po nekem določenem naèinu in ponovna združitev.
· Iskanje med zaporednimi razvrstitvami, ki so doloèene.
· Pregledovanje.
Nakljuèni naèini:
· Sluèajna inkrementalna metoda: Dodajanje elementov doloèenega niza enega za drugim brez znanega vrstnega reda.
· Nakljuèno deljenje in združevanje: Nakljuèna delitev niza in ponovna združitev.
· Iskanje med zaporednimi razvrstitvami, ki so nakljuène.
Slabost deterministiènih naèinov je v tem, da so težko prilagodljivi razmeram v veèdimenzionalnih prostorih. Celo v dvodimenzionalnem prostoru so lahko nakljuèni algoritmi uèinkovitejši kot deterministièni.
V tretjem poglavju so predstavljeni osnovni elementi raèunske geometrije in zakonitosti njihove postavitve na ravnini.
Osnovni element raèunske geometrije je toèka, ki je lahko postavljena:
· na premico pi = [ xi] Î R1,
· na ravnino pi = [ xi, yi] Î R2,
· v prostor pi = [ xi, yi, zi] Î R3.
Z razliènimi postavitvami in naèini združevanja teh toèk je mogoèe oblikovati ravninske in prostorske elemente. Na ravnini so to linijski segmenti in iz njih sestavljeni mnogokotniki. Mnogokotniki so obmoèja na ravnini, ki so od okolice razmejeni z nizom linijskih segmentov. Linijski segmenti ali robovi se med seboj dotikajo v temenih. Temena so lahko vboèena ali izboèena, kar vpliva na obliko mnogokotnika in na možnost postavitve diagonale med dve temeni. S postavljanjem diagonal v mnogokotnik se doseže triangulacija ali razdeljevanje na trikotnike. Mogoèi so še drugi naèini razdeljevanja mnogokotnikov: na trapeze, na konveksne površinske elemente. Razdeljevanje mnogokotnikov na površinske podelemente je izvedljivo s pomoèjo algoritmov. Na Sliki 1.4 je prikazan mnogokotnik z osemnajstimi temeni, preko katerega je izvedena triangulacija.
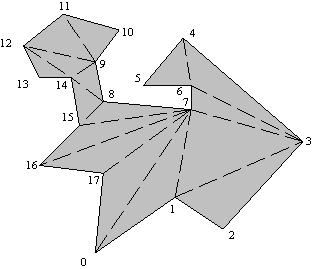
Slika 1.4 Mnogokotnik z n = 18 temeni.
V poglavjih 4 in 5 so predstavljene lupine na ravnini in v prostoru. Okoli niza toèk N na ravnini je mogoèe oviti ovoj, ki se dotika samo skrajnih toèk, medtem ko so vse ostale toèke v njegovi notranjosti. Te geometrijske forme se imenujejo lupine. Pri lupinah je pomembno, kako so predstavljene. Lupina je lahko prikazana kot niz neurejenih skrajnih toèk niza N, ki so med seboj sicer povezane, vendar ta povezava ni nakazana. Ali pa je lupina prikazana kot urejen niz skrajnih toèk niza v nasprotni smeri urinih kazalcev, ki so med seboj povezane z robovi. Unija vseh takih robov je lupina niza toèk N na ravnini.
Podobno velja tudi za niz toèk N v prostoru. Osnovni princip je enak: okoli vseh skrajnih toèk niza N v prostoru je potrebno oviti ovoj tako, da bodo vse toèke niza v njegovi notranjosti ali vsaj na njegovi meji. Pri predstavitvi prostorske lupine je dilema enaka kot na ravnini, le da je tu dodana možnost predstavitve s površinskimi elementi, ki se med seboj dotikajo v robovih in temenih, ki jih doloèajo skrajne toèke niza N.
Zgoraj povedano velja za konveksne lupine. Pri lupinah, ki niso nujno konveksne, navedeni opisi odpovejo, saj gre lupina lahko tudi skozi toèke, ki niso ekstremne, zaradi tega opisani naèin ovijanja ovoja okoli niza toèk N za nekonveksne lupine odpove. V nekonveksnih temenih je notranji kot > p . V tem primeru je potrebno lupino graditi na medsebojnih odnosih najbližjih si točk in upoštevati doloèene omejitve. Na Sliki 1.5 je prikazana nekonveksna lupina niza toèk N in konveksna lupina, kakršna bi nastala iz istega niza toèk N po naèinu ovijanja ovoja okoli vseh skrajnih toèk.
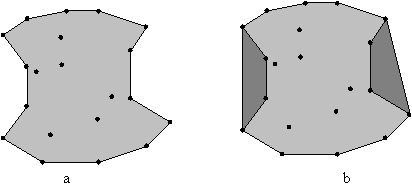
Slika 1.5 Lupina na ravnini. (a) Nekonveksna lupina; (b) konveksna lupina.
Enak problem nastane pri konstrukciji nekonveksene lupine v prostoru. Vsako nekonveksnost je potrebno prepoznati skozi postavitev prostorskih toèk oz. s pomoèjo doloèenih omejitev. Na Sliki 1.6 je prikazana konveksna lupina v 3D, ikozaeder. Sestavljen je iz dvajsetih trikotnikov, ki se med seboj dotikajo v dvanajstih temenih in tridesetih robovih. Njegova konstrukcija je mogoèa z ovijanjem ovoja okoli skrajnih toèk niza toèk N v prostoru.
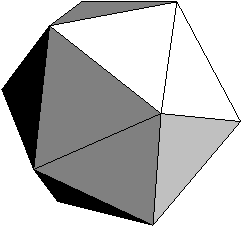
Slika 1.6 Konveksna lupina v 3D, ikozaeder.
Na ravnini je lupina sestavljena iz robov, ki povezujejo med seboj pare toèk. V prostoru je lupina sestavljena iz površinskih elementov: trikotnikov (Slika 1.6), kvadratov ali drugih mnogokotnikov. Površinske elemente se prilagaja namenu uporabe modela doloèenega telesa. Vrsti uporabljenih površinskih elementov je potrebno prilagoditi naèin odèitavanja toèk z modela. Pri trikotniških mrežah je možnosti postavitev trikotnikov več, vendar le ena daje najboljšo možno rekonstrukcijo površine. Na Sliki 1.7 je prikazano, kako postavitev trikotnikov med istimi štirimi točkami vpliva na površino. V tem primeru izbira vpliva tudi na konveksnost površine.
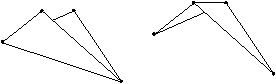
Slika 1.7 Razlièna postavitev trikotnikov za štiri toèke v prostoru.
V 6. poglavju so obravnavani odnosi med toèkami niza N, kar popisujejo Voronoi diagrami. Voronoi diagram ravnino razdeli tako, da v vsakem Voronoi obmoèju leži samo ena toèka niza N, rob tega obmoèja pa leži natanèno na polovici med dvema sosednjima toèkama. Omenjena lastnost vodi do najboljše možne triangulacije, ki se imenuje Delaunay-eva triangulacija in je v bistvu dvojnost Voronoi diagrama. Delaunayeva triangulacija zagotavlja tako razdelitev površine, da so vsi trikotniki kar se da "debeli", to pomeni, da imajo èim veèje notranje kote.
To lastnost je mogoèe v kombinaciji z ostalimi normativi uporabiti pri konstrukciji nekonveksne lupine v prostoru. Na Sliki 1.8 je prikazana Delaunayeva triangulacija in neka poljubna triangulacija za niz toèk N na ravnini.
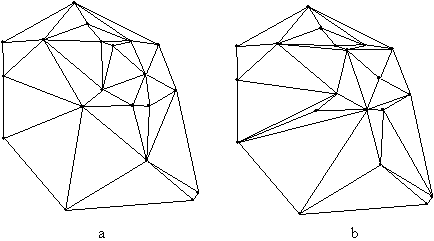
Slika 1.6 Triangulacija toèk na ravnini: (a) Delaunayeva; (b) poljubna.
V 7. poglavju je predstavljen sistem za zajemanje prostorskih toèk. Narejen je bil z namenom, da se pokaže možnost mehanskega zajemanja 3D točk, kar je bistveno ceneje od laserskega 3D skenerja. Uporabljeni elementi so najcenejši možni in prav tako izdelava. Zaradi tega je natanènost razmeroma slaba, a še vedno zadovoljiva za predstavitev delovanja sistema in kasneje za prikaz rekonstrukcije površine iz zajetih prostorskih toèk. Pokazana je prièakovana deformacija oblike zaradi nenatanènosti potenciometrov in v podpoglavju 7.6 dejanska deformacija valjaste oblike (Slika 1.8).
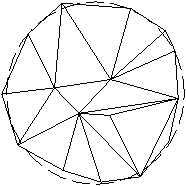
Slika 1.7 Deformacija valjastega dna.
A/D konverter digitalizira analogne podatke dobljene preko potenciometrov. Ta je povezan z raèunalnikom preko LPT porta. Prikazani sta sliki napajalnika konverterja in njegova povezava z raèunalnikom.
Digtalizirane podatke preèita program napisan v C, ki upošteva èasovni diagram A/D pretvorbe in jih sproti zapisuje v datoteko "tocke.dat". Diagram A/D pretvorbe je prikazan v podpoglavju 7.3.2.
Iz geometrije sistema in vrednosti na potenciometrih je mogoèe doloèiti koordinatne vrednosti toèke v prostoru.
V 8. poglavju je predstavljen celoten potek rekonstrukcije površine. Najprej osnovni elementi geometrije, ki so podrobneje opisani v 3. poglavju. V podpoglavju 8.2 je opisan princip triangulacije v 2D. Temelji na pregledovanju ravnine (uporabljen pri algoritmih opisanih v 3. poglavju) in lastnostih Delaunayeve triangulacije. To je predvsem lastnost najveèjega praznega kroga, ki je natanèneje opisana v podpoglavju 6.4.3. Postopek je zastavljen tako, da ga je mogoèe uporabiti tudi v prostoru, kar je prikazano v podpoglavjih 8.3 in 8.4. V podpoglavju 8.4 je natanèno opisan celoten postopek triangulacije oz. rekonstrukcije površine v 3D. V podpoglavju 8.5 sta prikazani vhodna in izhodna oblika rekonstrukcije in v podpoglavju 8.6 še nekaj primerov in naèinov uporabe rekonstrukcij. Na Sliki 1.8 je prikazana rekonstrukcija površine.
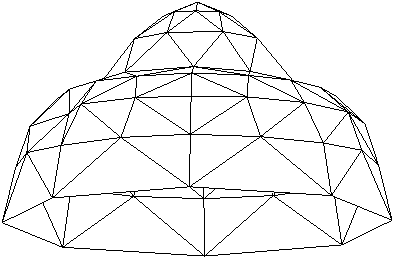
Slika 1.8 Rekonstrukcija površine.
2 GEOMETRIJA IN OSNOVE ALGORITMOV
2.1 Zgodovinska prièakovanja
Osnovna motiviranost k reševanju geometrijskih problemov izvira že iz starega Egipta in antič
ne Grèije.Za reševanje geometrijskih problemov je bil pomemben izum Evklidove strukture, to je sheme, ki na slogovno èist naèin vsebuje prepletanje algoritma in njegovega dokaza. Evklidova shema izpolnjuje vse, kar se zahteva od algoritma: je jasna, nedvoumna, natanèna in predvsem zakljuèena celota, ki da konèni rezultat. Shema je pomembna tudi zato, ker doloèa zbir orodij in operacij, ki se jih sme pri reševanju problemov uporabljati. Vprašanje, ki je v dobi reševanja problemov raèunske geometrije s pomoèjo raèunalnika še vedno aktualno je, ali je z Evklidovimi primitivi moè izpeljati do konca vse geometrijske "raèune". Nove mož
nosti reševanja so se pokazale, ko je Descartes predstavil koordinate in možnost prikazovanja geometrijskih problemov algebraično [3].
2.1.1 Kompleksnost v klasièni geometriji
Evklidove sheme so, razen za trivialne primere, zaradi nerazvitih primitivov, ki so dovoljeni, precej zapletene. Matematiki so se v kasnejših obdobjih precej posveèali vprašanju, kako zmanjšati število zaporedno potrebnih operacij na minimum, ki še vedno zagotavlja rešitev danega problema. Konèno število potrebnih operacij za rešitev problema predstavlja enostavnost rešitve oziroma merilo kompleksnosti. Tu pa je že podobnost s sodobno idejo èasovne kompleksnosti algoritma. Prav tako je vseskozi prisotno vprašanje prostora, ki ga potrebujemo za dokonèno rešitev problema.
2.2 Algoritem
V zadnjih petindvajsetih letih so se vzporedno z razvojem raèunalnikov pospešeno razvijali tudi algoritmi. Temeljna dela so v zaèetku sedemdesetih let pripomogla k sistematiziranemu uvajanju pravil, ki so v tem èasu prerasla v standard tega znanstvenega podroèja, ki se mu reèe raèunska geometrija.
Glavna elementa raèunske geometrije sta: algoritem in podatkovna struktura. Algoritmi so programi, ki jih je mogoèe izvajati na raèunalniku oziroma na primerni abstrakciji dejanskega raèunalnika. Podatkovne strukture so ureditve podatkov na naèin, ki v povezavi z algoritmi omogoèajo uèinkovito in elegantno rešitev raèunskih problemov.
2.2.1 Algoritem: Izraz in ovrednotenje uèinka
Algoritmi so oblikovani glede na doloèen naèin raèunanja; naèin raèunanja je primerna in zadostna abstrakcija fiziènega orodja - raèunalnika - na katerem se algoritem oziroma program izvaja. Ni potrebno niti zaželjeno, da se algoritmi pišejo v strojnem jeziku. Nasprotno, višji programski jezik Pidgin Algol, ki je standard na tem podroèju, teži k jasnosti, uèinkovitosti in zgošèenosti izraza. Pidgin Algol je neformalna in prilagodljiva oblika Algolu in njemu podobnim programskim jezikom. Jezik je precej strog pri kontrolnih strukturah, na drugi strani pa daje veliko svobode pri oblikovanju drugih izjav, kjer dopušèa obièajne matematiène izraze v povezavi z navadnim besednim izražanjem. Algoritem napisan v Pidgin Algolu je moè enostavno preoblikovati v katerikoli višji programski jezik [10].
Program se imenuje procedura in ima obliko
|
procedure ime ( parametri ) izjava. |
Izjava je lahko izpisana kot niz dveh ali veèih izjav, ki jih je potrebno med seboj združiti:
|
begin izjava;: : izjava end. |
Izjava je lahko oblikovana z navadnim besednim izrazom, ali pa z bolj formalno oblikovanim izrazom.
1. Prireditveni stavek:
|
spremenljivka := vir |
2. Pogojni stavek:
|
if pogoj then izjava ( else izjava ) |
3. Zanka, ki je lahko v eni od naslednjih oblik:
|
3a. for spremenljivka := vrednost until vrednost do izjava 3b. while pogoj do izjava 3c. repeat izjava until pogoj |
Razlika med while in repeat zankama je v tem, da je pri while-zanki pogoj testiran pred izvajanjem izjave, pri repeat-zanki pa je pogoj testiran kasneje.
4. Vrnitev vrednosti:
|
return izraz |
Izjava te vrste mora biti uporabljena v funkciji, ki je oblike
|
function ime ( parametri ) izjava. |
Izraz, ki ga vrne return, postane vir prireditvenega stavka, kot je pokazano v 1 zgoraj.
Vsi v nadaljevanju opisani algoritmi so oblikovani v Pidgin Algolu.
Èas, ki je potreben za izvršitev algoritma, je vsota vseh delnih èasov, v katerih se izvršijo posamezne opracije.Pri tem nas zanima tisti èas, ki je neodvisen od vrste raèunalnika, na katerem se algoritem izvaja ter predvsem, kako zahtevnost problema in kolièina vhodnih podatkov vplivata na èas izvajanja. Pri oblikovanju in analizi algoritma je potrebno za ovrednotenje izvajalnega èasa doloèiti število kljuènih operacij, ki se izvedejo. Ta naèin je uporaben pri doloèanju spodnje meje, pri èemer lahko vsaka neupoštevana for-zanka èas izvajanja samo poveèa. Pri doloèanju zgornje meje ta naèin ne da zadovoljivih podatkov. V tem primeru je potrebno upoštevati prav vse operacije, ki so se in ki bi se lahko izvedle v algoritmu. Sistem, ki opredeljuje spodnji, zgornji in vmesni èas izvajanja algoritmov je [10]:
·
O(f(N)) oznaèuje niz vseh funkcij g(N) tako, da obstajata pozitivni konstanti C in N0 ter da velja |g(N)|![]() Cf(N) za vse N
Cf(N) za vse N![]() N0.
N0.
·
W
(f(N)) oznaèuje niz vseh funkcij g(N) tako, da obstajata pozitivni konstanti C in N0 ter da velja g(N)![]() Cf(N) za vse N
Cf(N) za vse N![]() N0.
N0.
·
q
(f(N)) oznaèuje niz vseh funkcij g(N) tako, da obstajajo pozitivne konstante C1, C2 in N0 ter da velja C1f(N)![]() g(N)
g(N)![]() C2f(N) za vse N
C2f(N) za vse N![]() N0.
N0.
O(f(N)) tako oznaèuje funkcije, ki nikakor niso veèje kot nek konstanten èas f(N). Ta naèin se uporablja za oznaèevanje zgornje èasovne meje izvajanja. Nasprotno W (f(N)) oznaèuje funkcije, ki so vsaj tako velike kot nek konstanten èas f(N). Analogno se ta naèin uporablja za oznaèevanje spodnje èasovne meje izvajanja. q (f(N)) oznaèuje funkcije, ki so iste velikosti kot je f(N). Ta naèin se uprablja za doloèevanje "optimalnih" algoritmov.
Poleg èasa je drugo merilo kvalitete izvajanja algoritma prostor, ki je ponavadi definiran kot kolièina spomina, ki je potreben za izvedbo algoritma. Èasovna in prostorska kompleksnost sta tako dve glavni merili pri analizi izvajanj algoritmov. Pri izbiri algoritmov za posamezne aplikacije je potrebno upoštevati tudi dejstvo, da algoritem, ki je uspešen pri reševanju velikih problemov, ni nujno uspešen pri reševanju majhnih problemov, in obratno.
2.2.2 Podatkovne strukture
Algoritmi, ki se uporabljajo na podroèju raèunske geometrije, manipulirajo z objekti, ki niso na nivoju strojnega jezika. Podatke je zato potrebno urediti v èim preprostejšo strukturo, ki v povezavi z algoritmom omogoèa rešitev problema z raèunalnikom. Najpogosteje so podatki predstavljeni kot urejeni ali neurejeni nizi elementov.
Naj bo S niz elementov predstavljen s podatkovno strukturo in naj bo u poljubni element neke splošne množice, katere podmnožica je niz S. Glavne operacije, ki jih je mogoèe izvesti preko niza S, so:
1. MEMBER(u, S). Ali velja uÎ S? (možen odgovor da/ne.)
2. INSERT(u, S). Doda element u v niz S.
3. DELETE(u, S). Zbriše element u iz niza S.
Èe je { S1, S2, ..., Sk} zbir nizov, katerih medsebojni preseki so prazne množice, potem sta uporabni operaciji:
4. FIND(u). Vrne j, èe velja uÎ S
5. UNION(S
i, Sj; Sk). Združi niza Si in Sj in ga poimenuje Sk.
Kadar je doloèena splošna množica, so pomembne naslednje operacije:
6. MIN(S). Vrne najmanjši element niza S.
7. SPLIT(u, S). Razdeli niz S na { S
8. CONCATENATE(S
1, S2). Èe za poljubna u'Î S1 in u''Î S2 velja u'
Podatkovno strukturo si je abstraktno moè predstavljati kot premico, na kateri ima vsak podatek svojo toèko. V tem primeru je brisanje in dodajanje elementov povsem poljubno. Pri nekaterih aplikacijah se zahtevajo dodatne omejitve: elemente se dodaja na eni strani premice, briše se jih na drugi strani; brisanje in dodajanje elementov se izvaja na istem mestu. Neurejen niz je vedno mogoèe urediti upoštevaje lastnosti posameznih elementov oziroma s poimenovanjem elementov in abecednim razvršèanjem.
Pri raèunski geometriji je bilo potrebno obièajne podatkovne strukture prilagoditi specifiènosti problemov. Pri tem sta nastali nekonvencionalni strukturi DCEL (Double-Connected-Edge-List) in odsekovna drevesna struktura.
2.2.2.1 Podatkovna struktura DCEL
Struktura DCEL je primerna za predstavitev planarnih grafov na ravnini, kjer je G=(V, E) preslikava temen V
i v toèke na ravnini in Ei v povezave med temi toèkami tako, da se povezave med seboj ne sekajo, razen v svojih krajišèih. Planarni graf je tista oblika, pri kateri so povezave med toèkami ravni linijski elementi - robovi.Naj bo V={ v
1, ..., vn} in E={ e1, ..., en} . Graf predstavlja zaporedni zapis robov in temen, v katerih se robovi sekajo. Vsak rob je predstavljen natanèno enkrat. Primer DCEL podatkovne strukture je prikazan v Tabeli 2.1 in na Sliki 2.1 del planarnega grafa, ki ustreza podatkom v tabeli.
Tabela 2. 1: Primer DCEL podatkovne strukture.
|
V1 |
V2 |
F1 |
F2 |
P1 |
P2 |
|
|
1 |
||||||
|
2 |
||||||
|
: |
||||||
|
a1 |
1 |
2 |
1 |
2 |
a2 |
a3 |
|
: |
||||||
|
a2 |
4 |
1 |
1 |
|||
|
: |
||||||
|
a3 |
2 |
3 |
2 |
|||
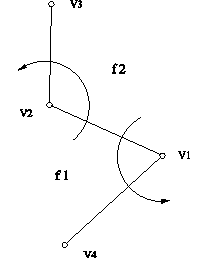
Slika 2.1 Del planarnega grafa za zgornjo DCEL podatkovno strukturo.
V prvih štirih poljih V1, V2, F1 in F2 so zapisani podatki, v zadnjih dveh poljih P1 in P2 so zapisani kazalci na podatkovna polja. V polju V1 je zapisano zaèetno teme roba, v polju V2 je zapisano konèno teme roba. V poljih F1 in F
2 sta zapisani imeni ploskev, ki ležita na levi in desni strani gledano iz V1 proti V2. Kazalec P1 kaže na rob, ki v nasprotni smeri urinih kazalcev z vrtiščem v V1 naslednji sledi robu (V1, V2). Podobno velja za kazalec P2, le da je tu vrtišèno teme V2.
V algoritmu opisanem v osmem poglavju je uporabljena poenostavljena struktura DCEL. Poenostavitev je potrebna, ker ne predstavlja planarnega grafa, ampak triangulacijo v prostoru.
2.2.2.2 Odsekovna drevesna struktura
Odsekovna drevesna struktura je statièno oblikovana za manipuliranje z odseki na realni osi, katerih ekstremi so del doloèenega niza na abscisi v obsegu [ 1, n] . Za celi števili l in r, za kateri velja l< r, odsekovna drevesna struktura T(l, r) nastaja: odsek v je sestavljen iz vrednosti B[ v] = l in E[ v] = r, pri èemer sta B zaèetek odseka in E konec odseka. Èe velja r-l> 1, potem je mogoèe odsek v preurediti v dva pododseka. V levega T(l, int((B[ v] +E[ v] )/2)) in desnega T(int((B[ v] +E[ v] )/2), r). Parametra B[ v] in E[ v] doloèata interval [ B[ v] , E[ v] ] Í [ l, r] v povezavi z odsekom v. Odsekovno drevesna struktura za l=4 in r=15 T(4, 15) je prikazana na Sliki 2.2.
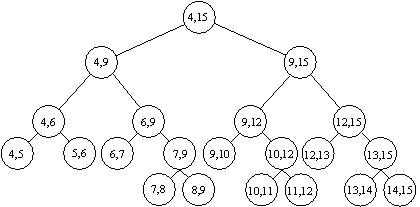
Slika 2.2 Odsekovna drevesna struktura T(4, 15).
2.3 Definicije osnovnih geometrijskih elementov
Elemetni, ki se uporabljajo za reševanje problemov s podroèja raèunske geometriji, so v glavnem toèke (niz toèk), ki so postavljene v evklidov prostor. Koordinatni sistem je doloèen tako, da je vsaka toèka predstavljena z vektorjem primerne dimenzije v kartezijevem koordinatnem sistemu. Za geometrijske elemetne ni nujno, da so sestavljeni iz konènega števila toèk, pomembno je, da te toèke zagotovijo konèno doloèljivost posameznega elementa. Tako velja, razen za toèko, ki doloèa sama sebe: premico doloèata dve poljubni toèki na njej, linijski segment doloèata toèki na njegovih krajišèih, ravnino doloèajo tri poljubne toèke te ravnine, mnogokotnik doloèa (urejen) niz toèk, itd. [ 7] .
Toèka. Toèko p glede na dimenzijo prostora doloèa (x
1, ..., xd) v Ed, pri èemer je Ed d-dimenzionalen evklidov prostor. Prav tako je toèko moè razumeti kot d-dimenzionalen vektor v Ed z vrhom v toèki p.
Premica. Dve razlièni toèki q
1 in q2 v Ed doloèata premico v tem prostoru kot linearno kombinacijo
a q1+(1-a )q2; (a Î R).
Bolj splošna oblika za k neodvisnih toèk pri (k![]() d) je
d) je
a 1q1+a 2q2+...+a k-1qk-1+(1-a 1-...-a k-1)qk; (a jÎ R, j=1,...k-1).
Linijski segment. Dve razlièni toèki q1 in q2 v Ed doloèata segment podobno kot premico, le da je potrebno zadostiti dodatnemu pogoju za koeficient a
a
q1+(1-a
)q2; (a
Î
R, 0![]() a
a
![]() 1).
1).
Taka kombinacija opisuje ravni linijski segment, ki povezuje toèki q1 in q2. Segment je lahko oznaèen tudi kot neurejen par ![]() .
.
Konveksen niz. Podroèje D v Ed je konveksno, èe je linijski segment ![]() med katerimakoli dvema toèkama q1 in q2 v Ed, v celoti v D.
med katerimakoli dvema toèkama q1 in q2 v Ed, v celoti v D.
Konveksna lupina. Konveksna lupina niza toèk S v Ed je meja okoli konveksnega niza in povezuje med seboj vse ekstremne toèke tega niza.
Mnogokotnik. V E2 je mnogokotnik doloèen kot konèen niz linijskih segmentov, ki se v parih dotikajo med seboj samo v svojih konènih toèkah. Linijski segmenti so robovi mnogokotnika, konène toèke pa temena mnogokotnika.
Planarni graf. Graf G=(V, E), pri èemer je V niz temen in E niz robov, je planarni, èe se ga da položiti na ravnino, ne da bi prekrival sam sebe. Planarni graf doloèa razdelitev ravnine oziroma podroèja na ravnini na manjša podpodroèja.
Triangulacija. Razdelitev ravninskega podroèja je triangulacija, èe so vsa njegova podpodroèja trikotniki. Triangulacija je planarni graf z najveèjim možnim številom robov, pri èemer se niti dva med seboj ne smeta sekati.
Polieder. V E3 je polieder doloèen s konènim nizom mnogokotnikov v prostoru, pri èemer se po dva in dva mnogokotnika med seboj dotikata samo v skupnem robu. Temena in robovi mnogokotnikov so hkrati tudi temena in robovi poliedra.
3 Mnogokotniki
V raèunski geometriji imajo velik pomen t.i. mnogokotniki. Z njimi je mogoèe popisovati objekte v realnem svetu, hkrati pa so primerni za raèunalniško obdelavo. Po zgradbi so lahko povsem enostavni (tak je s tremi linijskimi elementi trikotnik), lahko pa so sestavljeni iz veè tisoè elementov. Veèje, kompleksnejše mnogokotnike je ponavadi potrebno razstaviti na veè enostavnejših.
3.1 Definicija mnogokotnika
Mnogokotnik je obmoèje na ravnini, ki je od okolice razmejeno z nizom linijskih elementov. Topološko gledano je mnogokotnik homeomorfièna oblika kroga, oziroma njegova deformacija.
Naj bodo v
0, v1, v2, ..., vn-1 toèke na ravnini, naj bodo e0 = v0v1, e1 = v1v2, ..., ei = vivi+1, ..., en-1 = vn-1v0 linijski segmenti, ki povezujejo toèke na ravnini med seboj. Obojih je n in doloèajo mnogokotnik, èe [8]:
1. Je v krožnem redu preseč
išèe med dvema sosednjima linijskima segmentoma ena sama skupna toèka: eiÇ ei+1 = vi+1, za vse i = 0, ..., n-1.2. Se nesosednji segmenti ne sekajo med seboj: e
iÇ ej = Æ , za vse j¹ i+1.
Prvi pogoj doloèa mnogokotniku podobnost krogu zaradi krožnega stikanja linijskih segmentov med seboj po sistemu konec z zaèetkom, drugi pogoj pa definira enostavnost mnogokotnikov.
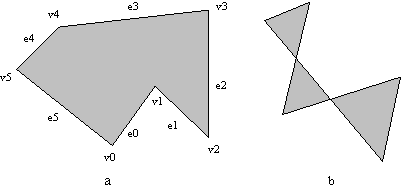
Slika 3.1 Mnogokotnik: (a) enostaven mnogokotnik - oznaèevanje temen in robov v nasprotni smeri urinih kazalcev; (b) neenostaven mnogokotnik.
Mnogokotniki, ki ne zadošèajo tema dvema pogojema, so neenostavni mnogokotniki (Slika 3.1b). Toèke na ravnini v so temena mnogokotnika, linijske povezave med njimi (temeni) e so robovi mnogokotnika. Vsak enostaven mnogokotnik P razdeli ravnino na dva dela. Meja mnogokotnika P je d P. Velja d PÍ P.
3.2 Triangulacija - razdeljevanje na trikotnike
Pri reševanju geometrijskih problemov s pomoèjo mnogokotnikov, je te potrebno veèkrat deliti na manjše, enostavnejše mnogokotnike. Osnovna delitev je delitev na trikotnike ali t.i. triangulacija. Glavno vprašanje, ki se pri tem zastavlja je, ali je na trikotnike mogoèe razdeliti vsak mnogokotnik.
Obstoj triangulacije je tesno povezan z obstojem diagonale v mnogokotniku. Postavitev diagonale v mnogokotnik je mogoèa le, èe ima mnogokotnik vsaj eno izboèeno teme. Iz tega sledijo trije logièni zakljuèki:
1. Vsak mnogokotnik mora imeti najmanj eno izboèeno teme.
2. Vsak mnogokotnik z n![]() 4 temeni ima diagonalo.
4 temeni ima diagonalo.
3. Vsak mnogokotnik P z n temeni se da razdeliti na trikotnike (triangulirati) z dodajanjem diagonal.
3.2.1 Obstoj izboèenega temena
Za dokaz prve postavke je potrebno privzeti mejo d P mnogokotnika P kot pot, po kateri hodi hodec v nasprotni smeri urinih kazalcev. Vsak njegov obrat v levo oznaèuje izboèeno teme mnogokotnika, vsak njegov obrat v desno pa vboèeno teme mnogokotnika. Naj bo L premica, ki teèe skozi najnižje teme mnogokotnika v
; najnižje glede na koordinato y. Èe je takih temen veè, naj bo to najbolj desno, najnižje teme. notranjost mnogokotnika P je nad premico L. V temenu v hodec naredi obrat v levo, kar pomeni, da ima vsak mnogokotnik najmanj eno izboèeno teme (Slika 3.2).
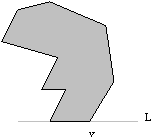
Slika 3.2
V najbolj desnem, najnižjem temenu se hodec obrne v levo; teme v je izboèeno.3.2.2 Obstoj diagonale
Naj bosta a in b temeni mnogokotnika P, ki ležita na meji mnogokotnika d
P pred in za temenom v. Èe daljica ab meje mnogokotnika d
P ne seka, niti se je ne dotika, potem je ab nedvoumno diagonala mnogokotnika. Èe pa se daljica ab dotika ali seka mejo mnogokotnika d
P, potem za ta mnogokotnik velja n![]() 4, v trikotniku D
avb pa je še najmanj eno teme mnogokotnika P, ki ni
4, v trikotniku D
avb pa je še najmanj eno teme mnogokotnika P, ki ni ![]() ,
, ![]() ali
ali ![]() . Naj bo x teme mnogokotnika P v trikotniku D
avb, ki je najbližje temenu v v pravokotni smeri na ab. Tako je teme x prvo teme, ki ga zadane premica L, ko se pomika iz temena v proti daljici ab (L |
|
ab). V prostoru D
avb, ki je omejen s premico L (temno senèeno na sliki), ni nobene toèke meje mnogokotnika d
P, razen temena x. Tako je daljica vx gotovo diagonala mnogokotnika P (Slika 3.3).
. Naj bo x teme mnogokotnika P v trikotniku D
avb, ki je najbližje temenu v v pravokotni smeri na ab. Tako je teme x prvo teme, ki ga zadane premica L, ko se pomika iz temena v proti daljici ab (L |
|
ab). V prostoru D
avb, ki je omejen s premico L (temno senèeno na sliki), ni nobene toèke meje mnogokotnika d
P, razen temena x. Tako je daljica vx gotovo diagonala mnogokotnika P (Slika 3.3).
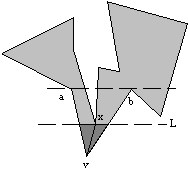
Slika 3.3 vx mora biti diagonala mnogokotnika P.
3.2.3 Obstoj triangulacije in njene lastnosti
Dokaz o obstoju diagonale posredno dokazuje, da se da vsak mnogokotnik razdeliti na trikotnike. Naj bo d = ab diagonala mnogokotnika P. Po definiciji diagonala d seka mejo mnogokotnika d
P samo v svojih krajišèih. Diagonala d razdeli mnogokotnik P na dva manjša mnogokotnika P', ki imata vsak manj kot n temen, in s tem postane del meje novih mnogokotnikov d
P' (Slika 3.4). V vsakem mnogokotniku P' (èe velja n'![]() 4) je mogoèe poiskati novo diagonalo d' = ef, ki mnogokotnik P' razdeli na dva nova manjša mnogokotnika. Tako deljenje je mogoèe ponavljati, dokler zaèetni mnogokotnik P ni razdeljen na same trikotnike.
4) je mogoèe poiskati novo diagonalo d' = ef, ki mnogokotnik P' razdeli na dva nova manjša mnogokotnika. Tako deljenje je mogoèe ponavljati, dokler zaèetni mnogokotnik P ni razdeljen na same trikotnike.
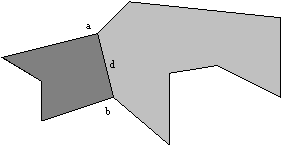
Slika 3.4 Diagonala ab razdeli mnogokotnik P na dva manjša mnogokotnika.
Triangulacijo preko mnogokotnika je mogoèe narediti na veè naèinov, število katerih narašèa s številom temen n. Za vse velja, da je za triangulacijo mnogokotnika P potrebno n - 3 diagonal, ki mnogokotnik P razdelijo na n - 2 trikotnikov.
3.2.4 Dualnost triangulacije
V teoriji grafov ima pomembno mesto t.i. dualnost ali dvojnost grafa. Gre za lastnost, da je doloèene podatke moè predstaviti na veè naèinov (dva-dualnost). Triangulacija mnogokotnika P je ponavadi predstavljena z vrisanimi diagonalami, lahko pa tudi z grafom T, ki je druga oblika predstavitve istih podatkov. Graf T, dualnost triangulacije mnogokotnika, je graf drevesne oblike, ki je sestavljen iz vozlišè in povezav med njimi. Vozlišèa predstavljajo trikotnike triangulacije, povezave med njimi pa skupne stranice trikotnikov triangulacije oziroma digonalo, ki je skupna dvema trikotnikoma (Slika 3.5).
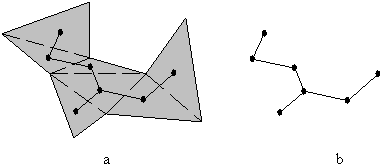
Slika 3.5 Dualnost triangulacije: (a) triangulacija mnogokotnika; (b) graf T.
Velja, da je graf T sestavljen iz vozlišè, v katerih se stikajo najveè tri povezave, in povezav med njimi. Vozlišèa grafa T stopnje ena so konène toèke grafa T oziroma uhlji poligona P. Vozlišèa druge stopnje ležijo na veji T in jo podaljšujejo. Vozlišèa tretje stopnje so razvejišèa grafa T. Iz povedanega sledi, da ima vsak mnogokotnik z n![]() 4 temeni vsaj dva neprekrivajoèa se uhlja.
4 temeni vsaj dva neprekrivajoèa se uhlja.
3.3 Površina mnogokotnika
Pri raèunanju površin mnogokotnikov si je mogoèe pomagati s triangulacijo. Mnogokotnik je potrebno razdeliti na trikotnike, izraèunati površino posameznih trikotnikov in vsota vseh je površina mnogokotnika.
3.3.1 Vektorski produkt
V splošnem je površina trikotnika osnovnica krat višina polovic. Vendar v pogojih, ko so podana temena a, b, c trikotnika T na ravnini, ta formulacija ni veè primerna. V tem primeru je uporaben vektorski produkt, katerega velikost predstavlja površino paralelograma s stranicama A in B. Polovica paralelograma je trikotnik s stranicama A in B, pri èemer velja A = b - a in B = c - a. Vektorski produkt je izraèunljiv s pomoèjo determinante:
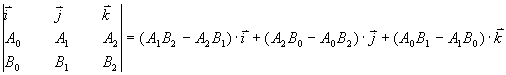 .
.
![]() ,
, ![]() in
in ![]() so enotski vektorji v x, y in z smeri. V dvodimenzijskem prostoru velja A2 = B2 = 0, od zgornjega izraza ostane (A0B1 - A1B0)×
so enotski vektorji v x, y in z smeri. V dvodimenzijskem prostoru velja A2 = B2 = 0, od zgornjega izraza ostane (A0B1 - A1B0)×
![]() . Površina trikotnika T(a, b, c) je:
. Površina trikotnika T(a, b, c) je:
A
(T) = 0.5(A0B1 - A1B0),2
A (T) = a0b1 - a1b0 - a1c0 - a0c1 - b0c1 - c0b1
ali
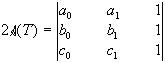 .
.
3.3.2 Površina konveksnega mnogokotnika
Vsak konveksen mnogokotnik je mogoèe trivialno razdeliti na trikotnike tako, da se eno krajišèe vseh diagonal d pripne v eno teme v
k (Slika 3.6).
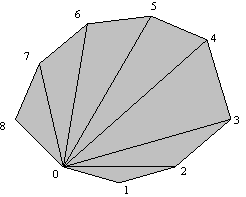
Slika 3.6 Tiangulacija konveksnega mnogokotnika; vse diagonale imajo eno skupno krajišèe v
0.
Površina tako razdeljenega poligona, ki ima temena oznaèena v nasprotni smeri urinih kazalcev z v
0, v1, ..., vn-1, je lahko zapisana kot
A
(P) = A (v0, v1, v2) + A (v0, v2, v3) + ... + A (v0, vn-2, vn-1).
3.3.3 Površina štiristranega konveksnega mnogokotnika
Ker je razdeljevanje na trikotnike izvedljivo na veè naèinov, je tudi površino mnogokotnika mogoèe zapisati na veè naèinov. Naj bo Q = (a, b, c, d) štiristrani konveksni mnogokotnik, ki ga je mogoèe triangulirati na dva naèina (Slika 3.7).
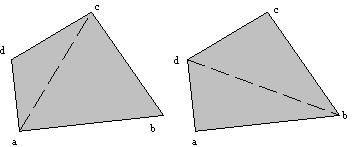
Slika 3.7
Dve možni triangulaciji štiristranega konveksnega mnogokotnika.
V prvem primeru velja
A
(Q) = A (a, b, c) + A (a, c, d)
2
A (Q) = a0b1 - a1b0 + a1c0 - a0c1 - b0c1 - c0b1 + a0c1 - a1c0 + a1d0 - a0d1 + c0d1 - d0c1,
po ureditvi:
2
A (Q) = a0b1 - a1b0 + c0d1 - d0c1.
Do enakega izraza pripelje raèunanje površine tudi v drugem primeru. Razvidno je, da izraz ne vsebuje segmenta ad, kar pomeni, da postavitev diagonale ne vpliva na konèni rezultat
A (Q).Èe so temena v
i štiristranega konveksnega mnogokotnika popisana s koordinatama xi in yi, je splošna enaèba za izraèun dvojne površine mnogokotnika enaka
![]() .
.
3.3.4 Površina štiristranega nekonveksnega mnogokotnika
Pri nekonveksnem štiristranem mnogokotniku (Slika 3.8) je možen en sam nač
in triangulacije. Diagonala ac je izven poligona, ostane le ab. Površina mnogokotnika je
A
(Q) = A (a, b, c) + A (a, c, d).
Zaradi lastnosti vektorskega produkta je površina D acd negativna in se od D abc odšteje. Tako prej omenjena enaèba za izraèun površine štiristranih konveksnih mnogokotnikov velja tudi za štiristrane nekonveksne mnogokotnike.
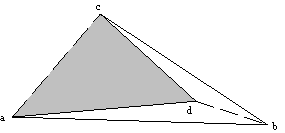
Slika 3.8 Nekonveksen mnogokotnik; senèena površina
A (a, c, d) je negativna.
Izkaže se, da je enač
ba za izraèun površine štiristranih mnogokotnikov splošna in velja tudi za mnogokotnike n
3.3.5 Površina mogokotnika, raèunana iz poljubnega centra
Pri posplošitvi omenjenega naèina, pri katerem se seštevajo površine trikotnikov, naj bo izhodišèe toèka ![]()
A
(T) = A (p, a, b) + A (p, b, c) +A (p, c, a).
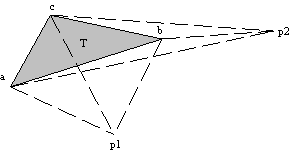
Slika 3.9 Površina trikotnika doloèljiva preko dveh zunanjih izhodišènih toèk p
1 in p2.
Naj bo izhodišèna toèka p = p
1 (Slika 3.9). Potem je prvi èlen enaèbe za izraèun površine A (p1, a, b) negativen zaradi svoje orientiranosti; ostala dva èlena sta pozitivna. Površina A (p1, a, b) predstavlja natanko tisto površino štiristranega mnogokotnika (p1, b, c, a), ki je zunaj trikotnika T. Tako je konèna površina natanèno A (T). Podobno velja tudi za izhodišèno toèko p = p2. Obe površini, A (p2, a, b) in A (p2, b, c) sta zaradi svoje orientiranosti negativni in se od A (p2, c, a), ki je pozitivna, odštejeta. Ostanek je natanèno A (T). Podobno velja za katerokoli poljubno toèko na ravnini, znotaj ali zunaj trikotnika T.
3.4 Izvedba triangulacije
3.4.1 Diagonala - notranja ali zunanja
Pri triangulaciji je potrebno najprej poiskati diagonalo mnogokotnika. Diagonala razdeli mnogokotnik na dva dela. Postopek je potrebno ponavljati, dokler mnogokotnik ni razdeljen na same trikotnike. Da je daljica v
ivj, i¹ j diagonala mnogokotnika P, mora veljati dvoje: da ne seka meje mnogokotnika d P in, da je v vsej svoji dolžini v notranjosti mnogokotnika P. Diagonale mnogokotnika se med seboj ne sekajo.Doloèanje diagonal [8] je preprosta aplikacija, ki se ponavlja, dokler niso doloèene vse diagonale mnogokotnika: za vsak rob e mnogokotnika P, ki se ne dotika nobenega krajišèa diagonale s, se preveri, èe e seka s. Ko je ugotovljeno preseèišèe med e in s, daljica s ni diagonala mnogokotnika. Èe noben tak rob ne seka s, potem je s diagonala mnogokotnika P. V primeru kolinearnosti toèk ta naèin ni uspešen (Slika 3.10).
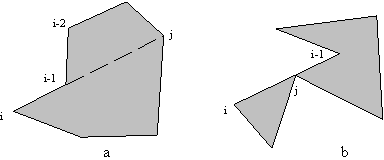
Slika 3.10 Teme, sosednje i, je kolinearno z ij.
Èe je rob vivi-1 kolinearen z vivj, potem vivj ni diagonala mnogokotnika. Naj bo rob mnogokotnika e = (vi-1, vj) kolinearen z vivj. Mogoèa sta primera, ko je daljica vivj daljša od e; pri j¹ i-1 (Slika 3.10a) in ko je daljica vivj krajša od e (Slika 3.10b), vendar to ni veè enostaven poligon.
Vzporedno z aplikacijo doloèanja diagonal je potrebno za vsako diagonalo preveriti, èe ne seka druge diagonale. To se preveri z medsebojnim primerjanjem koordinat krajišè obeh diagonal. Na koncu je potrebno za vsako diagonalo preveriti, ali leži v notranjosti mnogokotnika P.
Vprašanje notranjosti in zunanjosti je test lokalne narave. Èe je diagonala s = vivj v okolici temen vi in vj v notranjosti mnogokotnika P, potem je v notranjosti mnogokotnika v vsej svoji dolžini. Diagonala v vsej svoji dolžini namreč ne seka meje mnogokotnika d P. Zadostno je testiranje ene same konène toèke diagonale. Èe je diagonala s v okolici toèke vi v notranjosti mnogokotnika, potem je v notranjosti mnogokotnika tudi v okolici toèke vj in obratno. Podobno velja tudi za zunanjost. Test se tako zoži na pregled okolice točke vj. Možna sta primera, ko je teme v vj izboèeno (Slika 3.11a) ali vboèeno (Slika 3.11b).
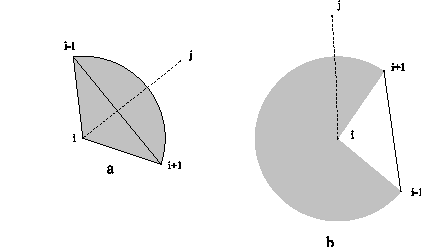
Slika 3.11 Diagonala s = ij izhaja iz trikotnika doloèenega s temeni v
i-1, vi, vi+1: (a) i je izboèeno teme;(b) i je vboèeno vboèeno teme.
Na sliki 3.11a je diagonala ij s krajišèem v izboèenem temenu v
i. Jasno je, da je diagonala v notranjosti mnogokotnika P, èe je v notranjosti trikotnika z vrhom v temenu vi. To pomeni, da mora biti teme vi-1 na levi strani diagonale vivj in teme vi+1 ne levi strani vjvi. Ta pogoj se preverja s pomoèjo raèunanja površine med temeni i, j in i-1 ter i, i+1 in j. Èe je površina (raèunana s pomoèjo vektorskega produkta) pozitivnega predznaka, potem predpostavka levega drži, če je negativnega predznaka, predpostavka levega ne drži.V primeru vboèenosti temena i ta naèin odpove, saj sta lahko temeni i-1 in i+1 hkrati obe na desni strani, hkrati obe na levi strani ali vsako na svoji strani diagonale ij. Podobnost s primerom a je ta, da je notranjost pri izboèenem temenu enaka zunanjosti pri vboèenem temenu. Notrajnost in zunanjost sta zamenjani. Pri drugem primeru torej velja (test po istem naèinu kot pri izboèenem temenu), èe diagonala ni zunanja, potem je notranja. Testira se zunanjost. Pred testiranjem notranjosti oziroma zunanjosti je tako potrebno doloèiti, ali je teme v
i izboèeno ali vboèeno. Teme vi je izboèeno, èe je teme vi+1 na levi strani ali na robu vi-1vi. Po dogovoru je teme vi, pri katerem je notranji kot enak
3.4.2 Triangulacija z odstranjevanjem ušes
Zgoraj opisani postopek triangulacije mogokotnikov se ne uporablja prav pogosto, saj je zaradi vsakokratnega pregledovanja pravilnosti diagonale precej poèasen.
Hitrejši je naèin, pri katerem se postavlja diagonalo med temeni v
i in vi+2, pri èemer mora biti vi+1 izboèeno teme. Imenuje se naèin odstranjevanja ušes mnogokotnika [8]. Po definiciji ima vsak mnogokotnik z nTriangulacija se zaène v izhodišènem temenu v
0. Poiskati je potrebno prvo trojico vi, vi+1, vi+2, (uhelj mnogokotnika), t.j. izboèeno teme z vrhom v vi+1. Ko je taka trojica najdena, je daljica vi, vi+2 gotovo diagonala mnogokotnika. Trikotnik vi, vi+1, vi+2 se 'odreže' od preostanka mnogokotnika. Postopek se ponavlja, dokler od mnogokotnika ne ostane samo (zadnji) trikotnik. Triangulacija po načinu odrezovanja ušes je s tem konèana (Slika 3.12). Izhoden podatek je seznam diagonal, ki so definirane z lastnimi krajišèi glede na oznaèevanje vhodnega podatka mnogokotnika (Tabela 3.1).
Tabela 3.1: Izhodni podatek: seznam diagonal za sliko 3.12.
|
Diagonale: |
||||
|
1 - 3 |
3 - 7 |
9 - 11 |
9 - 14 |
7 - 15 |
|
4 - 6 |
1 - 7 |
9 - 12 |
8 - 14 |
7 - 16 |
|
3 - 6 |
0 - 7 |
12 - 14 |
8 - 15 |
7 - 17 |

Slika 3.12 Mnogokotnik razdeljen na trikotnike po naèinu odstranjevanja uhljev.
3.5 Razdeljevanje na trapeze
Poleg razdeljevanja na trikotnike, je mnogokotnik mogoèe razdeliti tudi na trapeze (na konveksne površinske elemente). Ta razdelitev je lahko osnova za nadaljnje razdeljevanje na trikotnike. Razlika med triangulacijo in razdeljevanjem na trapeze je ta, da so pri prvi razdelitvi razdelitveni elementi diagonale, pri drugi razdelitvi pa so razdelitveni elementi horizontalne ali verikalne (horizontalna ali vertikalna trapezna dekompozicija) linije skozi temena v, ki so pri dekompoziciji mnogokotnika omejene z njegovo mejo d P (Slika 3.13), pri dekompoziciji ureditve èrt pa s èrtami samimi ali pa se nadaljujejo v neskonènost (Slika 3.14). Na Sliki 3.13 je prikazana vertikalna trapezna dekompozicija. Pri horizontalni trapezni dekompoziciji so razdelitvene èrte postavljene horizontalno.
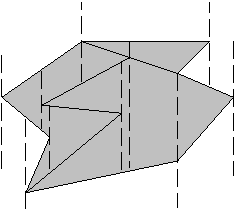
Slika 3.13 Vertikalna trapezna dekompozicija.
3.5.1 Trapezna dekompozicija s pregledovanjem ravnine
Razdeljevanje na trapeze je izvedljivo s pomoèjo razliènih deterministiènih ali nakljuènih inkrementalnih algoritmov. Pri deterministiènem naèinu gre za pregledovanje poligona oziroma planarnega grafa s pomoèjo horizontalne ali vertikalne linije [7]. Èe je pregledovalna linijo vertikala, potem koordinata x predstavlja èas, v katerem se pregledovalna linija L pomika od x = -¥ proti x = +¥ . Naj bo N niz n-tih linearnih segmentov na ravnini (Slika 3.14).
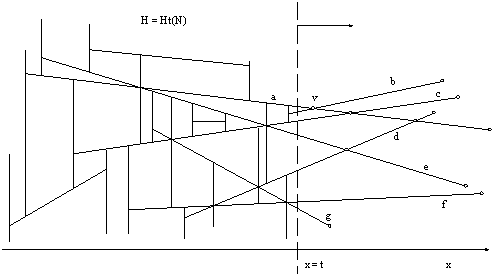
Slika 3.14 Pregledovanje ravnine z vertikalno linijo L.
Naj bo rezultat trapezne dekompozicije H(N). Naj bo H
t(n) presek med polravnino x
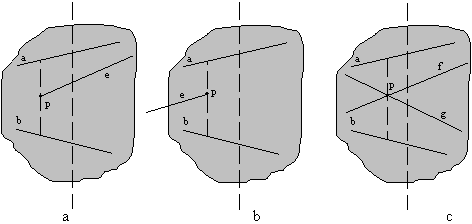
Slika 3.15 Pregledovanje (a) leve krajišène toèke linijskega segmenta e; (b) desne krajišène toèke linijskega segmenta e; (c) preseèišèa med linijskima segmentoma g in f.
1. Karakteristièna toèka p je levo krajišèe linijskega segmenta eÎ N. V tem primeru se segment e doda mejnemu seznamu. Segmenta a in b, za katera se predpostavi, da vedno obstajata (lahko se ju umetno doda nad in pod vse ostale segmente niza N), sta v popravljenem mejnem seznamu pred in za segmentom e. V tem trenutku se spremeni tudi H
2. Karakteristièna toèka p je desno krajišèe linijskega segmenta eÎ N. V tem primeru se segment e zbriše iz mejnega seznama. V H
t(n) se doda vertikalna povezava med segmentoma a in b, ki gre skozi karakteristièno toèko p. Segmenta a in b postaneta v popravljenem mejnem seznamu sosednja. Èe se sekata ne desni strani toèke p, je to preseèišèe natanèno doloèljivo. Ob predpostavki, da ga v popisu dogodkov še ni, se novo preseèišèe tja vpiše.
3. Karakteristièna toèka p je preseèišèe dveh linijskih segmentov e, fÎ N. V popravljenem mejnem seznamu segmenta f in g zamenjata mesti. Popravi se H
t(n), kamor se vpiše preseèišèe p in vertikalna povezava med segmentoma a in b, ki gre skozi karakteristièno toèko p. V popravljenem mejnem seznamu sta sedaj sosednja segmenta a in f ter b in g. Za oba para je potrebno preveriti obstoj preseèišèa desno od karakteristiène toèke p (kot opisano v toèki 1.) in ob predpostavki, da ga v popisu dogodkov še ni, se novo preseèišèe tja vpiše.
3.5.2 Inkrementalni algoritem trapezne dekompozicije
Inkrementalni algoritem trapezne dekompozicije [7] temelji na dodajanju linijskih segmentov v niz N po nakljuènem vrstnem redu. Za vsak na novo dodan linijski segment se dodajo karakteristiène vertikale, ki so del trapezne dekompozicije. Naj bo N niz n linijskih segmentov na ravnini (Slika 3.16) in H(N) konèni rezultat razdelitve na trapeze (Slika 3.17). H(N) nastaja inkrementalno z dodajanjem segmentov iz niza N, enega za drugim po nakljuènem vrstnem redu. V i-tem koraku algoritma je zgrajen H(N
i), pri èemer Ni predstavlja niz prvih i nakljuèno izbranih linijskih segmentov. Na Sliki 3.18 je prikazana trapezna dekompozicija za prve štiri linijske segmente.
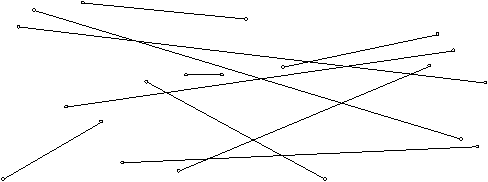
Slika 3.16 N: niz n linijskih segmentov na ravnini.
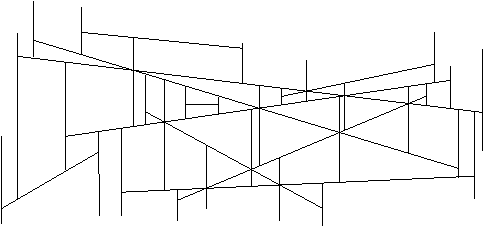
Slika 3.17 H(N): konèni rezultat trapezne dekompozicije.
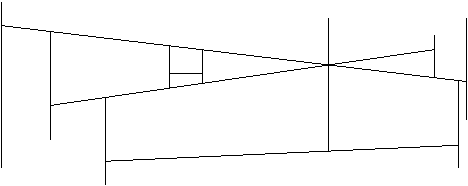
Slika 3.18 Trapezna dekompozicija H(N
4) za prve štiri linijske segmente.
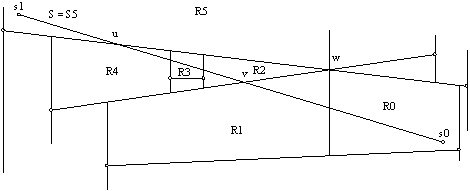
Slika 3.19
Potovanje vzdolž linijskega segmenta S = S5 od toèke s0 proti toèki s1v razdelitvi H(N4).
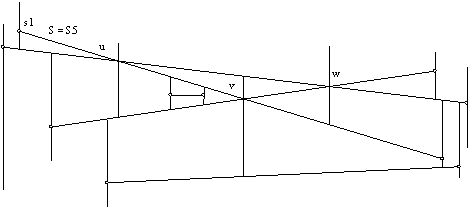
Slika 3.20 H'(N
4) = H(N5).
Naj bo H(N
4) trapezna dekompozicija po štirih dodanih linijskih segmentih. Naj bo toèka s0 eno dveh krajišè linijskega segmenta S = S5. Predpostavimo, da toèka s0 leži v trapezu, ki je v H(N4) že določen. Za doloèitev karakteristiènih toèk je potrebno pregledati vse že doloèene trapeze R0, R1, ... v H(N4), preko katerih gre novododani linijski segment S5. Potrebno je potovati vzdolž linijskega segmenta S = S5 od krajišèa s0 proti krajišèu s1 in pri tem pregledovati obmoèja R0, R1, ... (Slika 3.19). Naj bo f katerikoli trapez v H(Ni), ki ga linijski segment Si+1 seka. V vsakem pregledanem trapezu je potrebno ugotoviti karakteristiène toèke (Slika 3.20) in skozi njih dodati vertikale (za vertikalno dekompozicijo).
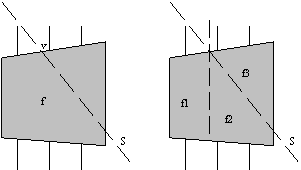
Slika 3.21 Razdeljevanje trapeza f.
Kaj se dogaja, ko linijski segment S
i+1 seka že določene trapeze, je prikazano na Sliki 3.21. Èe linijski segment
3.6 Razdeljevanje mnogokotnikov na konveksne površinske elemente
Mnogokotnike je mogoèe, poleg triangulacije in razdelitve na trapeze, razdeliti tudi na konveksne površinske elemente. Pri tem se je potrebno držati dveh naèel:
1. Razdeliti mnogokotnik na èim manj konveksnih površinskih elementov.
2. Izvesti to razdelitev v èim krajšem èlasu.
Ti dve naèeli si nasprotujeta. Tako se možne rešitve razdeljevanja razlikujejo po tem, katero od obeh naèel je upoštevano v veèji meri. Poiskati je potrebno kompromisno rešitev med obema naèeloma.
Dekompozicijo mnogokotnika P je mogoèe narediti s postavljanjem diagonal ali s postavljanjem linijskih segmentov. Razlika je v tem, da so krajišèa diagonal vedno temena v mnogokotnika P, za segmente pa je pomembno samo to, da njihova krajišèa ležijo nekje na meji mnogokotnika d P. Delitev s pomoèjo segmentov je precej bolj zapletena, vendar ponuja optimalnejše rezultate.
Teorem (Chazzele) [8] pravi:
Naj bo F
najmanjše število konveksnih površinskih elementov. Za mnogokotnik z r vboèenimi temeni velja, ![]() .
.
Èe se skozi temena, ki imajo notranji kot >
p
(vboèeno), potegnejo diagonale, nujno nastaneta dva konveksna površinska elementa. Število takih elementov je r + 1. Z eno diagonalo je torej mogoèe dobiti najveè dva taka elementa. Rezultat je ![]() konveksnih elementov (Slika 3.22, Slika 3.23).
konveksnih elementov (Slika 3.22, Slika 3.23).
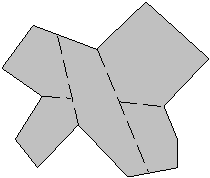
Slika 3.22 r + 1 konveksnih elementov: r = 4; 5 elementov.
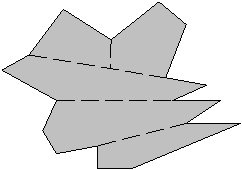
Slika 3.23 ![]() konveksnih elementov: r = 7; 5 elementov.
konveksnih elementov: r = 7; 5 elementov.
Tako dekompozicijo je mogoèe dobiti z odvzemanjem nepomembnih diagonal. Diagonala d je za teme v nepomembna, èe njena odstranitev ne ustvari površinskega elementa, ki bi bil v temenu v vboèen. Teme v mora biti tako v vsakem primeru vboèeno. Vsako vboèeno teme ima najveè dve pomembni diagonali. Diagonala, ki ni pomembna za nobeno teme, je nepomembna digonala.
Algoritem je preprost. Najprej je potrebno mnogokotnik P razdeliti na trikotnike in po vrsti odvzemati vse nepomembne diagonale. Na Sliki 3.24 je prikazano vboèeno teme v. Sosednji temeni sta v
+ in v-. Levo od v-, v je polravnina H-, desno od v, v+ je polravnina H+. Na polravnini H+ je lahko najveè ena pomembna diagonala. Èe sta diagonali dve, je tista, ki je bližja (v, v+), nepomembna. Njena odstranitev ne povzroèi vboèenosti površinskega elementa v temenu v. Podobno velja tudi za polravnino H-.
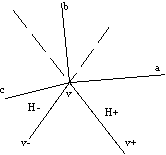
Slika 3.24 Pomembne diagonale. Diagonala a je nepomembna, saj diagonala b v polravnini H
+ še vedno zagotavlja izboèenost v temenu v. Podobno je tudi c nepomembna diagonala.
3.6.1 Optimalna konveksna razdelitev mnogokotnika
Razdeljevanje s segmenti je precej bolj zapleteno, vendar ponuja optimalnejše rezultate. Mogoèa je tudi delitev, pri kateri se delitveni segmenti s meje mnogokotnika d P ne dotikajo (Slika 3.25).
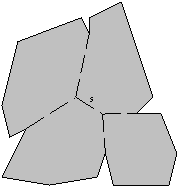
Slika 3.25 Optimalna konveksna razdelitev mnogokotnika.
3.7 Ravninski elementi v prostoru
Za popisovanje teles v prostoru se prav tako uporabljajo zgoraj našteti elementi, le da so njihove funkcije nekoliko spremenjene. Osnovni element je še vedno toèka, doloèena s tremi kordinatnimi vrednostmi in ne dvema, kot na ravnini:
toèka v prostoru p
i = [ xi, yi, zi] Î R3.
Mnogokotnik je še vedno obmoèje na ravnini, ki je lahko katerakoli ravnina v prostoru; razmejitev med notranjostjo in zunanjostjo mnogokotnika doloèa niz linijskih segmentov. Razmejitev med notranjostjo in zunanjostjo prostorskih teles pa ne doloèajo veè linijski segmenti mnogokotnika, ampak površinski elementi, ki jih ti mnogokotniki doloèajo. Naèeloma so lahko ti površinski elementi poljubni mnogokotniki, vendar so to ponavadi konveksni mnogokotniki, najveèkrat trikotniki ali konveksni štirikotniki.
Pri rekonstrukciji površine, opisani v 8. poglvju, so uporabljeni površinski elementi, ki loèujejo prostorsko notranjost od zunanjosti, Delaunayevi trikotniki.
4 Lupine v 2D
Èe gre pri mnogokotnikih v grobem za razdeljevanje ravnine na dva dela, t.j. na zunanjost in notranjost mnogok
otnika, so lupine že bolj kompleksne strukture. Ne samo, da predstavljajo eno osrednjih področij raèunske geometrije, temveè je z njimi mogoèe rešiti tudi velik del ostalih problemov, ki se pojavljajo z razvojem raèunske geometrije.Konveksna lupina je uporabna kot samostojna struktura, ali pa kot pripomoèek za graditev kompleksnejših oblik in preko tega za prouèevanje njihove geometrije in topologije.
Pojem konveksnosti je naèeloma doloèljiv nedvoumno, za prepoznavanje konveksnosti in konveksnih lupin pa kljub temu obstaja veè razliènih definicij. Nekatere izmed njih so:
1. Nizu elementov R
2. Konveksna lupina, sestavljena iz niza toèk N, je presek vseh polravnin, ki vsebujejo ta niz N.
3. Konveksna lupina, sestavljena iz niza toèk N na ravnini, je najmanjši konveksni mnogokotnik, ki obdaja niz N. V takem primeru ne obstaja noben manjši mnogokotnik P', za katerega bi veljalo P É P' Ê N.
4. Konveksna lupina, sestavljena iz niza toèk N na ravnini je unija vseh trikotnikov, ki jih doloèajo toèke niza N.
5. Konveksen niz toèk x
1,..., xk je vsota x1 + ... +xk , pri èemer mora veljati ai
Pri reševaju problemov s podroèja lupin je glavno vprašanje, kaj naj bo rezultat oz. kako naj bo oblikovan izhodni podatek. Naj bo N niz n-tih neurejenih toèk na ravnini. Kot izhoden podatek je možen seznam vseh skrajnih toèk niza N, ali pa doloèena meja mnogokotnika. Skrajne toèke niza N so temena konveksne lupine, meja mnogokotnika pa je konveksen mnogokotnik, ki niz toèk na ravnini s konveksno lupino omejuje - razmejuje od okolice. Razlika je v tem, da se s podatkom o meji dobi niz toèk, ki po vrstnem redu doloèajo lupino, ponavadi v nasprotni smeri urinih kazalcev, pri seznamu skrajnih toèk pa so ti podatki neurejeni.
4.1 Algoritem za konstrukcijo lupine v 2D
Za doloèanje konveksnih lupin obstaja cela vrsta algoritmov. V splošnem se delijo na deterministiène in nakljuène. Tu se pokaže prednost nakljuènih algoritmov, saj so v splošnem razširljivi na veèdimenzionalne prostore, medtem ko ni nujno, da bodo deterministièni algoritmi, ki so uporabni na ravnini, uporabni tudi v prostoru. Èe že, je lahko njihovo izvajanje zapleteno ali zelo poèasno. V nadaljevanju sta na kratko predstavljena po dva deterministièna in dva nakljuèna algoritma.
4.1.1 Deterministièen algoritem za konstrukcijo konveksne lupine v 2D
Pri prvem deterministiènem naèinu je potrebno konveksno lupino razdeliti na zgornjo in spodnjo verigo [7] (Slika 4.1).
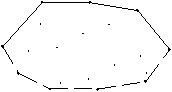
Slika 4.1 Zgornja in spodnja veriga.
Loènici med njima sta toèki z najmanjšo in najveèjo vrednostjo koordinate x. Toèke iz niza N je potrebno razporediti po narašèujoèi koordinati x. Glavna ideja je, da se nizu N
i, ki vsebuje prvih i že pregledanih točk, dodajajo naslednje toèke, za katere se preverja, ali ležijo na konveksni lupini ali v njeni notranjosti.Naj bo N
i niz prvih i toèk, naj bo U(Ni) zgornja veriga, ki je že določena v okviru Ni. Naslednja toèka, ki jo je potrebno pregledati, je p = pi+1. Zadnja, za katero je ugotovljeno, da je del verige U(Ni), naj bo toèka r. Iz toèke r je potrebno potovati po meji U(Ni) v levo in pregledovati že postavljene točke na zgornji verigi. Pri toèki q je pregledovanje konèano, saj leži naslednja toèka s pod linijo pq. Oèitno je, da je v zgornjo verigo U(Ni+1) potrebno pripisati povezavo med toèkama p in q ter zbrisati vse toèke iz že doloèene verige U(Ni), ki so desno od toèke q (Slika 4.2). Enak postopek je potrebno ponoviti še za doloèanje spodnje verige.
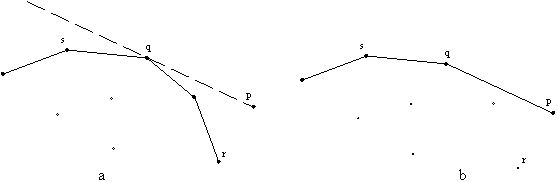
Slika 4.2 Dodajanje nove toèke. (a) U(N
i); (b) U(Ni+1).
Drugi deterministièen algoritem je znan kot Graham-ov algoritem [8]. Vhodni podatek je niz n-tih toèk N, za katerega je potrebno ugotoviti konveksno lupino. Ideja temelji na izbiri neke poljubne toèke x v notranjosti meje mnogokotnika in ureditvi vseh toèk niza N po narašèujoèem relativnem kotu v nasprotni smeri urinih kazalcev (Slika 4.3).
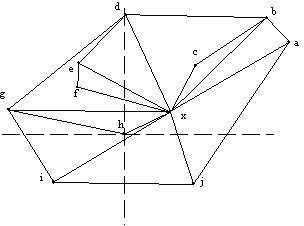
Slika 4.3 Toèka x je poljubna, ostale so oznaèene glede na narašèujoèi kot
; a
Naslednji korak je pregledovanje že urejenih toč
k na ravnini. Prvi toèki niza S, ki doloèa konveksne lupine, sta S = (a, b). Naslednja toèka, ki sledi glede na narašèujoèe kote, je toèka c. Konveksnost v vsaki toèki se doloèa z že omenjeno metodo hodca po meji mnogokotnika. Ker hodec po že postavljeni lupini naredi na poti a, b, c v toèki b zavoj v levo, je toèka b gotovo izboèeno teme in toèka c se pripiše nizu S = (a, b, c). Kot naslednjo je potrebno preveriti toèko d. Na poti b, c, d naredi hodec v temenu c zavoj v desno. To pomeni, da je c gotovo vboèeno teme in kot tako ne more biti del meje konveksnega mnogokotnika oz. konveksne lupine. Toèka c se iz niza S izbriše, vpiše se toèka d, S = (a, b, d). Ta postopek je potrebno ponavljati, dokler v nizu S prvi in zadnji element nista enaka; S = (a, b, d, e, g, i, j, a).Glavni problem je, da ni moè z gotovostjo trditi, da sta toèki a in b na meji konveksnega mnogokotnika oz. na konveksni lupini. Tako bi se v primeru, da nista, postopek preverjanja nadaljeval naprej, kljub temu, da je bil pregledan že ves niz N. Med zaèetkom in koncem niza S ne bi bilo logiène povezave.
Problem nastane tudi v primeru, èe je že v prvem koraku, pri trojici S = (a, b, c), ugotovljeno, da je teme b nedvoumno vboèeno, t.j. da hodec v tem temenu naredi obrat v desno. Toèka b tako ne more biti del niza S. V tem primeru je potrebno b iz niza S = (a, b) zbrisati. Ostane samo S = (a). Z eno samo toèko naslednje toèke ni mogoèe preverjati, potrebni sta najmanj dve.
Rešitev je, èe se za nakljuèno toèko x izbere najnižjo (po koordinati y) toèko niza N. Èe sta taki toèki dve, naj bo izbrana najbolj desna, najnižja toèka niza N. Zaporedno urejanje po narašèujoèih kotih je enako kot prej omenjeno. Glede na velikost relativnega kota naj bodo toèke zdaj oznaèene s p0, p1, ..., pn-1 v nasprotni smeri urinih kazalcev. V tem primeru je logièno,da so toèke p0, p1 in pn-1 na meji konveksnega mnogokotnika oz. na konveksni lupini. S tem sta odpravljena oba prej omenjena problema. Novo oznaèevanje in urejanje je prikazano na Sliki 3.4.
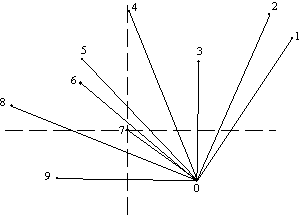
Slika 4.4 Osnova urejanja je toèka 0, (na Sliki 4.3 toèka j).
4.1.2 Nakljuèni algoritem za konstrukcijo konveksne lupine v 2D
Prvi nakljuèni algoritem temelji na dodajanju polprostorov Rd, v tem primeru polravnin R2, v ureditev H(N). H(N) predstavlja presek vseh že dodanih polravnin. Polravnina je najosnovnejša konveksna lupina. Presek konveksnih lupin da vedno novo konveksno lupino. Presek polravnin je torej konveksna lupina [7].
Naj bo N niz polravnin in H(Ni) konveksna lupina, t.j. presek vseh polravnin po dodani polravnini S = Si. Naslednji korak je dodajanje (i+1). polravnine S = Si+1 k ureditvi H(Ni) (Slika 4.5).
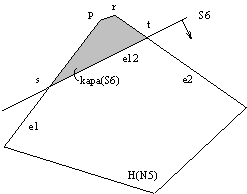
Slika 4.5 Dodajanje polravnine S = Si+1 k ureditvi H(Ni).
Ureditev H(Ni+1) bo nastala iz H(Ni) po odstranitvi kape i+1, ki je presek H(Ni) Ç
![]() , pri èemer je polravnina
, pri èemer je polravnina ![]() komplementarna polravnini S. Najprej je potrebno izbrati poljubno teme p Î
H(Ni), ki leži na komplementarni ravnini
komplementarna polravnini S. Najprej je potrebno izbrati poljubno teme p Î
H(Ni), ki leži na komplementarni ravnini ![]() i+1. Èe tako teme ne obstaja, se lahko ravnino S = Si+1 izpusti, saj ne vpliva na H(Ni+1) = H(Ni) Ç
Si+1. Èe tako teme obstaja, je potrebno pregledati robove ureditve H(Ni) in ugotoviti preseèišèi (vedno sta dve) med H(Ni) in mejo polravnine Si+1 (oziroma
i+1. Èe tako teme ne obstaja, se lahko ravnino S = Si+1 izpusti, saj ne vpliva na H(Ni+1) = H(Ni) Ç
Si+1. Èe tako teme obstaja, je potrebno pregledati robove ureditve H(Ni) in ugotoviti preseèišèi (vedno sta dve) med H(Ni) in mejo polravnine Si+1 (oziroma ![]() i+1).
i+1).
Pregledovanje H(Ni) se zaène v temenu p. Naj bo f prvi rob, ki ga je potrebno pregledati. Èe f v celoti leži na polravnini ![]() , potem ga je potrebno s pripadajoèima temenoma odstraniti. Prvi rob f, ki leži na
, potem ga je potrebno s pripadajoèima temenoma odstraniti. Prvi rob f, ki leži na ![]() samo delno, je hkrati tudi zadnji, ki ga je potrebno pregledati v tej smeri. Na Sliki 4.5 je to rob e1. Ta rob f se razdeli na dva dela tako, da se tisti del, ki leži na polravnini
samo delno, je hkrati tudi zadnji, ki ga je potrebno pregledati v tej smeri. Na Sliki 4.5 je to rob e1. Ta rob f se razdeli na dva dela tako, da se tisti del, ki leži na polravnini ![]() , izbriše, druga polovica pa je hkrati del ureditve H(Ni+1). Pregledovanje je potrebno ponoviti tudi v drugi smeri, da se ugotovi še drugi rob, ki leži hkrati na polravninah
, izbriše, druga polovica pa je hkrati del ureditve H(Ni+1). Pregledovanje je potrebno ponoviti tudi v drugi smeri, da se ugotovi še drugi rob, ki leži hkrati na polravninah ![]() in S. Drugi rob na Sliki 4.5 je e2. Od ureditve H(Ni) je potrebno odstraniti kapo, del d
Si+1, ki leži med obema odrezanima robovoma f, ki postaneta nova robova ureditve H(Ni+1). Tretji nov rob ureditve H(Ni+1) je rob polravnine Si+1, ki je na obeh koncih omejen z že določenima robovoma e1 in e2.
in S. Drugi rob na Sliki 4.5 je e2. Od ureditve H(Ni) je potrebno odstraniti kapo, del d
Si+1, ki leži med obema odrezanima robovoma f, ki postaneta nova robova ureditve H(Ni+1). Tretji nov rob ureditve H(Ni+1) je rob polravnine Si+1, ki je na obeh koncih omejen z že določenima robovoma e1 in e2.
Drugi nakljuèni algoritem je prav tako kot prejšnji inkrementalen, vendar gre v tem primeru za dodajanje toèk [8] (v prejšnjem primeru je šlo za dodajanje polravnin). Algoritem je uporaben tudi v veèdimenzionalnem prostoru, pri konstruiranju konveksnih lupin v 3D, kar je eno pomembnejših podroèij raèunalniške geometrije.
Osnovna ideja je dodajanje toèk ene za drugo h konveksni lupini, ki jo že doloèa prvih k dodanih toèk oziroma dodajanje toèke k obstojeèi konveksni lupini. Naj bo P = { p0, p1, ..., pn-1} niz toèk na ravnini. Prva konveksna lupina je trikotnik, sestavljen iz toèk konv{ p0,p1,p2} . Naj bo Q = Hk-1 in p = pk. Doloèanje konveksne lupine konv{ Q È p} se razširi na dve možnosti v odvisnosti ali p Î Q ali p Ï Q:
1. p Î Q. Èe je ugotovljeno, da leži toèka p v obmoèju Q, potem se jo lahko izpusti, saj ne vpliva na obliko konveksne lupine. Isto velja, èe toèka p leži na meji Q t.j. na d Q. Za doloèanje notranjosti oziroma zunanjosti se uporabi že omenjeno t.i. predpostavko levega (3.4.1). Za vsak rob konveksne lupine Q posebej se preverja ali je toèka na njegovi levi strani. Èe to velja preko cele meje obmoèja d Q, potem je toèka p v notrajnosti Q.
2. p Ï Q. Èe se za katerikoli rob izkaže, da predpostavka levega ne drži, potem velja p Ï Q in mogoèa je doloèitev konv{ Q È p} . Potrebno je poiskati dve tangenti, ki povezujeta toèko p in obmoèje Q in oblikovati novo konveksno lupino (Slika 4.6).
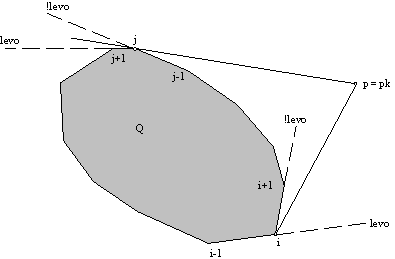
Slika 4.6 Tangenti od toèke p h Q; "levo" pomeni, da je toèka p levo od nakazane smeri in "!levo", da toèka p ni levo od nakazane smeri.
Tangenta, ki povezuje toèko pk z obmoèjem Q, se dotika meje konveksne lupine Q v eni sami toèki. Naj bo pi ena izmed takih toèk. Tudi v tem primeru se toèko lahko doloèi z uporabo predpostavke levega. Na Sliki 4.6 je vidno, da je toèka p levo od smeri pi-1pi in desno oziroma "nelevo" od smeri pipi+1. Za zgornjo tangento velja ravno obratno. Toèka p desno od smeri pj-1pj in levo od smeri pjpj+1. Sledi, da je toèka pj toèka tangente, èe se za dve sosednji toèki dobi drugaèen rezultat predpostavke levega. Ostane še konstrukcija nove konveksne lupine, ki je (p0, p1, ..., pi-1, pi, p, pj, pj+1, ..., pn-1) .
4.2 Nekonveksna lupina niza toèk na ravnini
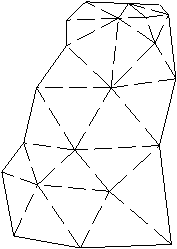
Slika 4.7 Lupina niza toèk N, n = 21.
Na Sliki 4.7 je prikazana nekonveksna lupina niza toèk N. Narejena je s pomoèjo algoritma, ki je opisan v osmem poglavju, in predstavlja projekcijo toèk v prostoru na ravnino. Èrtkani robovi med posameznimi toèkami niza N predstavljajo Delaunayevo triangulacijo.
5 Konveksne lupine v 3D
Na ravnini je konveksna lupina doloèena kot ovoj, ki se ga lahko ovije okoli vseh ekstremnih toèk niza N tako, da so vse toèke niza v notranjosti ovoja ali vsaj na njegovi meji (te so ekstremne toèke niza N). Lupina je torej sestavljena iz toèk na ravnini (temen), ki so med seboj povezane z linijskimi segmenti (robovi). Tudi v prostoru je lupina ovoj, ki ga je mogoèe oviti okoli vseh ekstremnih toèk niza N tako, da so vse prostorske toèke v njegovi notranjosti ali vsaj na njegovi meji. V prostoru je lupina sestavljena iz množice toèk (temen), ki so med seboj povezane z linijskimi segmenit (robovi), ti pa med seboj tvorijo ploskve. Temena robov so hkrati tudi temena ploskev. Podobno kot je lupina v 2D doloèena kot presek polravnin R
2, je konveksna lupina v 3D doloèena kot presek polprostorov R3.
5.1 Polieder
Polieder je naravno posploševanje ravninskega mnogokotnika v prostor, je obmoèje v prostoru, katerega meja vsebuje konèno število veèstranih ploskev, ki so lahko nepovezane, ali pa se med seboj dotikajo v robovih in temenih. Ta definicija je precej nejasna, še posebej, kadar ima opraviti z lupinami na splošno.
Meja poliedra je sestavljena iz treh vrst geometrijskih objektov: nièdimenzionalnih temen (toèke), enodimenzionalnih robov (linijski segmenti) in dvodimenzionalnih površin (mnogokotniki). Površino poliedra je mogoèe natanèno oznaèiti z odnosi med posameznimi geometrijskimi elementi. Pri tem so upoštevani trije pogoji: elementi se morajo med seboj sekati "pravilno", lokalna topologija mora biti "pravilna", globalna topologija mora biti "pravilna" [8].
1. Elementi se sekajo "pravilno".
Za vsak par ploskev se zahteva, ali
(a) se med seboj ne dotikata, ali
(b) imata eno skupno teme, ali pa
(c) imata dve skupni temeni in en skupen rob, ki ti dve temeni povezuje med seboj.
Nepravilno sekanje je torej prediranje ploskev in napaèno dotikanje ploskev med seboj (Slika 5.1). S tem, ko so doloèena preseèišèa med ploskvami, so doloèena tudi preseèišèa med robovi in temeni.
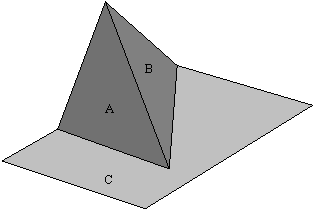
Slika 5.1 Ploskev B prebada ploskev C; ploskvi A in C se dotikata napaèno.
2. Lokalna topologija je "pravilna".
Lokalna topologija popisuje površino v okolici toèke. Tehnièno se ta omejenost popiše, da naj bo okolica vsake toèke na površini homeomorfièna disku. Homeomorfnost dopušèa raztezanje in upogibanje, ne dopušèa pa pretrganja (Slika 5.2).
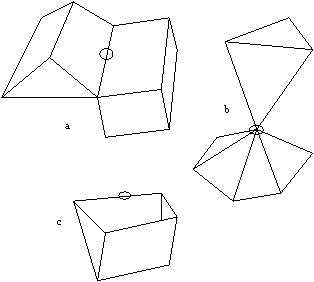
Slika 5.2 Telesa na sliki niso poliedri. V vseh treh primerih okolica toèke ni homeomorfièna disku: (a) toèka leži hkrati na dveh ploskvah; (b) triangulacija ne da enostavno zaprte povezave med elementi; (c) objekt ni zaprt, okolica toèke je pol disk.
3. Globalna topologija je "pravilna".
Površina mora biti zvezna, zaprta in omejena. To pomeni, da namišljeni hodec lahko prehodi katerokoli pot med katerikolima toèkama na tej površini. V tem smislu so dovoljeni tuneli oziroma razliène udrtine v lupino. Obravnavanje konveksnih lupin ne zajema teh dveh pojavov.
Upoštevaje vse skupaj sledi: meja poliedra je konèen zbir ravninskih, konveksnih, omejenih poligonov na naèin, da:
1. se ploskve sekajo pravilno,
2. je okolica vsake toèke homeomorfièna oblika diska oziroma, da je povezava med temeni preprosta poligonalna veriga,
3. da je površina zvezna.
Meja je torej zaprta in obdaja oziroma omejuje obmoèje prostora. Vsak rob si delita natanèno dve ploskvi, ki se imenujeta sosednji. Za konveksen polieder velja, da je segment, ki povezuje katerikoli toèki poliedra v notranjosti tega poliedra. Konveksnost je popisljiva tudi z notranjimi koti. Notranji kot med dvema sosednjima ploskvama je vedno ![]()
Pravini poliedri so tisti, katerih ploskve so skladni, pravilni mnogokotniki: enakostranièen trikotnik, kvadrat, pravilni petkotnik, itd. Število ploskev, ki se stikajo v enem temenu je enako za vsa temena pravilnega poliedra. Obstaja samo pet znaèilno pravilnih poliedrov, kar je prvi odkril Platon [8]. Èe je p število temen na ploskev in v število ploskev, ki se dotikajo v temenu, mora za pravilni polieder veljati ( p - 2 ) ×
( v - 2 ) ![]() 3 (Slika 5.3). V Tabeli 5.1 so prikazane vrednosti za pravilne poliedre.
3 (Slika 5.3). V Tabeli 5.1 so prikazane vrednosti za pravilne poliedre.
Tabela 5.1: Seznam vrednosti p in v.
|
p |
v |
(p-2)(v-2) |
ime |
opis |
|
3 |
3 |
1 |
tetraeder |
trije trikotniki na teme |
|
4 |
3 |
2 |
kocka |
trije kvadrati na teme |
|
3 |
4 |
2 |
oktaeder |
štirje trikotniki na teme |
|
5 |
3 |
3 |
dodekaeder |
trije petkotniki na teme |
|
3 |
5 |
3 |
ikozaeder |
pet trikotnikov na teme |
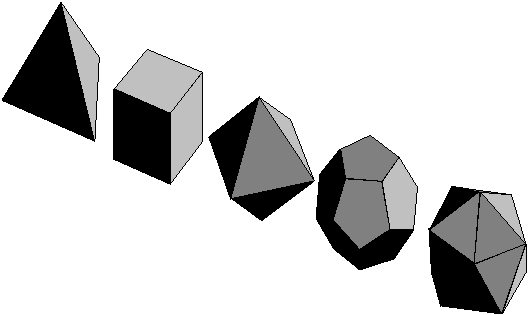
Slika 5.3 Pravilna Platonova telesa.
Medsebojen odnos med številom temen, robov in ploskev popisuje Eulerjeva formula
V - E + F = 2 (Tabela 5.2).
Tabela 5.2: Število temen, robov in ploskev petih pravilnih poliedrov.
|
Ime |
(p, v) |
V |
E |
F |
|
tetraeder |
(3, 3) |
4 |
6 |
4 |
|
kocka |
(4, 4) |
8 |
12 |
6 |
|
oktaeder |
(3, 4) |
6 |
12 |
8 |
|
dodekaeder |
(5, 3) |
20 |
30 |
12 |
|
ikozaeder |
(3, 5) |
12 |
30 |
20 |
5.2 Inkrementalni algoritem za konstrukcijo konveksne lupine v 3D
Iz množice toč
k je mogoèe doloèiti polieder s pomoèjo inkrementalnega algoritma. Prej opisani algoritem je zadostoval za konstrukcijo konveksne lupine iz množice toèk na ravnini, naslednji pa omogoèa konstruiranje konveksne lupine iz množice toèk v prostoru [8].Glavna ideja je identièna: pri i-tem dodajanju toèke je potrebno doloèiti H
i Ü konv(Hi-1 È pi). Problem doloèanja se razdeli na dva dela. Naj bo toèka p = pi in Q = Hi-1. Ugotoviti je potrebno, èe velja p Î Q. Èe to drži, se lahko toèko p izpusti, èe ne, je potrebno doloèiti 'stožec', ki je tangenten na Q in ima vrh v toèki p ter skonstruirati novo konveksno lupino. Test p Î Q se izvede podobno kot v dveh dimenzijah. Toèka p je v notranjosti Q, èe je p na pozitivni strani vsake izmed ploskev, ki doloèajo lupino Q. Testiranje predpostavke levega omogoèa volumen tetraedra, kakor to pri dveh dimenzijah omogoèa površina trikotnika. Èe je toèka p v notranjosti lupine Q, morajo imeti vsi volumni enak predznak. Problem nastane, kadar je toèka zunaj lupine Q, saj je potrebno le to spremeniti.V ravninskem primeru je bilo potrebno poiskati dve tangenti med toèko p in lupino Q
. V prostoru pa tangentne linije zamenjajo tangentne ploskve. Te ploskve skupaj oblikujejo stožčasto telo, ki je sestavljeno iz trikotnih ploskev, katerih skupni vrh je v toèki p, osnova pa rob e na lupini Q. Iz toèke p je nekaj ploskev na Q vidnih, nekaj pa nevidnih. Vse tiste ploskve, ki so vidne je potrebno odstraniti pri spreminjanju Q = Hi-1 v Hi. Robovi vidnosti postanejo osnova za konstrukcijo stožca z vrhom v točki p. Rob e na lupini Q je torej tak rob, da je ploskev, ki povezuje e s p, tangenta na Q. Rob e je soseden dvema ploskvama. Ena teh je iz toèke p vidna, druga ne. Rob e je torej na meji med vidnim in nevidnim delom Q.Podobno je mogoèe p razumeti kot izvor svetlobe. Del lupine Q bo osvetljen, drugi del pa bo ostal v senci. Rob e je tista linija, ki loèuje osvetljeni del od senènega.
V nadaljevanju algoritma je potrebno poiskati vse ploskve, ki so vidne iz toèke p. To se ugotovi s pomoèjo volumna, ki ga doloèajo toèke na lupini Q, to je trojica (a, b, c) in toèka p. Èe je ploskev (a, b, c) iz toèke p vidna, potem je volumen tetraedra (a, b, c, p) gotovo negativen. Taka ploskev se odstrani, H
i pa se oblikuje iz nevidnega dela lupine in ploskovne povezave med mejnim robom e in toèko p. V naslednjem koraku se izbere novo toèko p = pi in celoten postopek preverjanja in ponovnega konstruiranja se ponovi, dokler niso pregledane vse toèke niza N v prostoru.
Osnovni algoritem za raèunalniško konstrukcijo lupine v 3D iz niza toèk:
procedure: 3D inkr_alg(i)
begin pripisati H
4 tetraedru (p0,p1,p2,p3);for i := 4 until i < n do
begin
for za vsako ploskev f stopnje H
i-1 dobegin
vol := vol (f, p
i);if vol < 0 then f je vidna
if nobena ploskev vidna then
izloèiti p
i; (* je v notranjosti Hi-1 *)else
for za vsak mejni rob e stopnje H
i-1 dobegin
konstrukcija ploskve e,p
i;end.
for za vsako vidno ploskev f do
begin
briši f;
end.
Popravi H
i;end.
end.
end.
V višjih dimenzijah postanejo problemi bolj zapleteni in težje predstavljivi. "Hiperprostor" si je najlaže predstavljati, č
e si znamo predstavljati preskoke iz nièdimenzionalnega prostora v enodimenzionalen in naprej v dvo in trodimenzionalnen prostor.
5.3 Višje dimenzije
Predstavljanje prve, druge in tretje dimenzije je preprosto. Problem nastane pri višjih dimenzijah. Najboljši je postopen pristop skozi nižje dimenzije. Točka na številski premici je predstavljena z eno samo številko: je vrednost oziroma lokacija. Lahko se razume kot enodimenziinalen objekt, saj leži na premici, ki je enodimenzionalen element. Toč
ka v dveh dimenzijah je doloèljiva z dvema koordinatama (x, y), v treh dimenzijah pa s tremi (x, y, z). Iz tega sledi, da so za toèko v štirih dimenzijah potrebne štiri koordinate (x, y, z, t). Èe se prve tri koordinate (x, y, z) razumejo kot prostorske koordinate in t kot èas, potem vse štiri skupaj predstavljajo dogodek v prostoru in èasu. Poleg prostor-èasa obstaja še veè možnih izpeljav višjih dimenzij. Ena izmed njih je primer hiperkocke. Nièdimenzionalna kocka je toèka. Enodimenzionalna kocka je daljica. Dvodimenzijska kocka je kvadrat. Tridimenzionalna kocka je normalna kocka v prostoru. Pri tem veljajo naslednji podatki:
Tabela 5.4: Izpeljava toèke v višje dimenzije.
|
Dimenzija |
Ime |
Vd |
Ed |
|
0 |
toèka |
1 |
0 |
|
1 |
daljica |
2 |
1 |
|
2 |
kvadrat |
4 |
4 |
|
3 |
kocka |
8 |
12 |
|
4 |
hiperkocka |
16 |
31 |
|
d |
d-kocka |
2d |
2Ed-1+Vd-1 |
V
je število temen in E število robov.Kocka v d dimenzijah je zgrajena iz dveh kock (druga je kopija prve) dimenzije d-1. Èe se enodimenzionalno kocko (toèko) raztegne v drugo dimenzijo, nastane dvodimenzionalna kocka, daljica. Èe se to naprej raztegne v smeri pravokotno sebi, nastane kvadrat. Èe se kvadrat preslika na ravnino, ki je vzporedna prvi, nastane kocka (Slika 5.4). Èe se kocko z osmimi temeni in dvanajstimi robovi preslika v nov položaj in obe kocki poveže z osmimi robovi, nastane t.i. hiperkocka (Slika 5.5). To je kocka v četrti dimenziji. Koordinate temen (vseh je šestnajst) predstavljajo konveksno lupino (Slika 5.6).
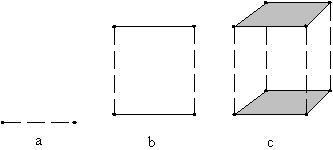
Slika 5.4 Kocka kot kvadrat potegnjen v tretjo dimenzijo.
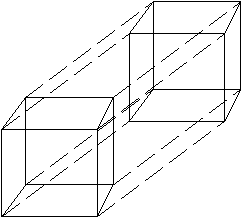
Slika 5.5 Hiperkocka kot kocka potegnjena v èetrto dimenzijo.
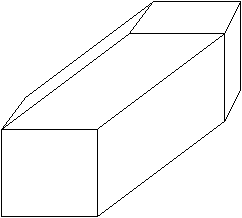
Slika 5.6 Konveksna lupina hiperkocke.
5.4 Nekonveksna lupina niza toèk v prostoru
Iz toèk v prostoru je mogoèe doloèiti tudi nekonveksno lupino. V tem primeru zoraj opisani algoritmi odpovejo, saj vsako toèko, ki doloèa lokalno konkavnost, postavijo v notranjost lupine. Za konstrukcijo nekonveksne lupine (Slika 5.7) je bil uporabljen algoritem, opisan v poglavju osem.
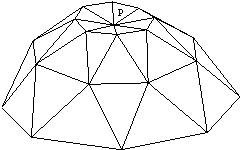
Slika 5.7 Lupina v prostoru z lokalno konkavnostjo okoli toèke p.
6 Voronoi diagram
Voronoi diagrami obravnavajo sosedske odnose med toèkami niza N: katera toèka je kateri najbližja, katera je od katere najbolj oddaljena, itd.
6.1 Definicija voronoi diagrama
Naj bo P = { p
1, p1, ..., pn} niz toèk na ravnini. Voronoi diagram V(pi) ravnino razdeli tako, da je diagram V(pi) sestavljen iz vseh toèk, ki so vsaj tako blizu toèki pi, kot so blizu katerikoli drugi toèki pk [8]:
V(p
i) = { x: ½ pi - x½
Naj bosta na ravnini samo dve toèki p
1 in p2. Naj bo premica B(p1, p2) = B12, ki pravokotno razdeli segment p1p2 na dva enaka dela. Potem je vsaka toèka x na premici B12 enako oddaljena od toèke p1, kakor tudi od toèke p2. Velja: ½ p1x½ = ½ p2x½ (Slika 6.1).
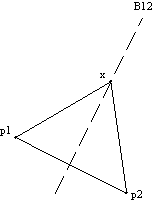
Slika 6.1 Dve toèki na ravnini: ½ p1x½ = ½ p2x½ .
Èe ležijo na ravnini tri toèke (p1, p2, p3), te definirajo trikotnik. Razpolovnice stranic trikornika B12, B23 in B31 se sekajo v toèki, ki je središèe oèrtanega kroga (Slika 6.2). Ta toèka ni nujno v notranjosti trikotnika.
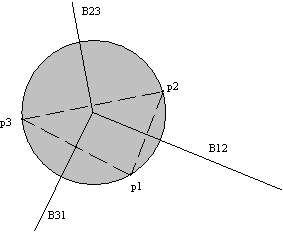
Slika 6.2 Tri toèke na ravnini: razpolovnice se sekajo v središèu trikotniku oèrtanega kroga.
Iz zgoraj omenjenih primerov je razvidno, da imajo razpolovnice Bij pomembno vlogo pri prouèevanju odnosov med toèkami na ravnini. Naj bo H(pi, pj) zaprta polravnina, ki je omejena z Bij in vsebuje toèko pi. Potem se lahko H(pi, pj) razume kot niz vseh toèk, ki so bliže toèki pi kot toèki pj. Kot že omenjeno, je V(pi) niz toèk, ki so bliže toèki pi, kot katerikoli drugi toèki ali z drugimi besedami, to so toèke, ki so bliže pi kot p1, bliže pi kot p2, bliže pi kot p3, itd. Upoštevaje navedeno je mogoèe napisati enaèbo za Vornoi diagram V(pi):
V(pi) = ![]() H(pi,pj),
H(pi,pj),
pri èemer je potrebno upoštevati presek preko vseh i in j, za katere velja i¹ j. Iz enaèbe sledi lastnost Voronoi diagrama: obmoèja Voronoi diagrama so konveksna, ker nastanejo kot preseèišèa veèih polravnin. Kadar so ta obmoèja omejena, so to konveksni poligoni. Robovi se imenujejo Voronoi robovi in temena Voronoi temena. Katerakoli toèka na Voronoi robu ima dve najbližji točki niza toèk na ravnini, Voronoi teme pa ima najmanj tri najbližje take toèke.
V primeru štirih toèk na ravnini, ki oblikujejo vogale kvadrata, je to Voronoi diagram kot je prikazano na Sliki 6.3a. Voronoi teme je v tem primeru èetrte stopnje. Èe se eno toèko nekoliko premakne (Slika 6.3b), postane diagram normalen. Prvi primer je izrojen zaradi centriènega položaja štirih toèk na ravnini.
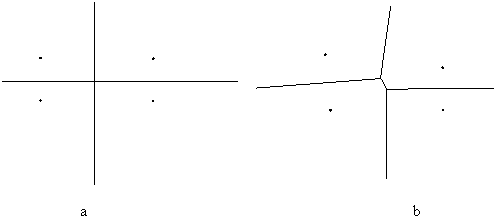
Slika 6.3 Izrojen (a) in normalen (b) Voronoi diagram.
Voronoi diagram V(pi) za i = 20 toèk na ravnini bi izgledal kot na Sliki 6.4.
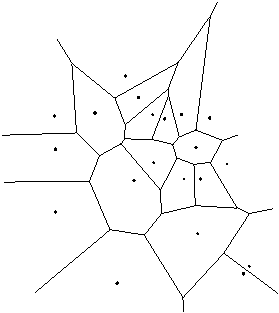
Slika 6.4 Voronoi diagram za i = 20 toèk na ravnini.
6.2 Delaunayeva triangulacija
Delaunayeva triangulacija nastane takrat, kadar se med seboj povežejo toč
ke na ravnini, ki imajo skupen Voronoi rob. Delaunayeva triangulacija D(P) in Voronoi diagram V(P) predstavljata dvojnost; isti podatki so predstavljeni na dva razlièna naèina.Na Sliki 6.4 je prikazan Voronoi diagram za dvajset toèk na ravnini. Na Sliki 6.5 je prikazana Delaunayeva triangulacija za teh istih dvajset toèk. Na Sliki 6.6 sta prikazana Delaunayeva triangulacija in Voronoi diagram skupaj.
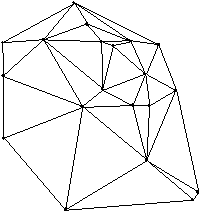
Slika 6.5 Delaunayeva triangulacija za iste toèke na ravnini kot na Sliki 6.4.
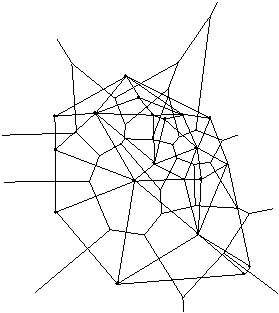
Slika 6.6 Delaunayeva triangulacija in Voronoi diagram: Sliki 6.4 in 6.5 skupaj.
6.2.1 Odnos med Delaunayevo triangulacijo in Voronoi diagramom
Za razumevanje obeh, v raèunski geometrijij pomembnih struktur D(P) in V(P), je potrebno poznati odnos med njima [8]. Naj bo P nespremenljiv niz toèk na ravnini.
Za Delaunayevo triangulacijo veljajo lastnosti:
D1. D(P) je ravnoèrtna dvojnost V(P), po definiciji.
D2. D(P) je triangulacija, èe ne obstajajo štiri centriène toèke na ravnini: vsaka površina je trikotnik. Ploskve D(P) so Delaunayevi trikotniki.
D3. Vsak trikotnik grafa D(P) ustreza temenu grafa V(P).
D4. Vsak rob grafa D(P) ustreza robu grafa V(P).
D5. Vsak vozel grafa D(P) ustreza obmoèju grafa V(P).
D6. Meja D(P) je konveksna lupina
D7. Notranjost trikotnikov D(P) ne vsebuje nobenih toèk niza P.
Za Voronoi diagram veljajo lastnosti:
V1. Vsako Voronoi obmoèje V(p
V2. V(p
i) je neomejen, èe je pi na konveksni lupini niza toèk P.V3. Èe je Voronoi teme na stièišèu V(p
1), V(p2) in V(p3), potem je v središèu kroga C(v), ki ga doloèajo toèke p1, p2 in p3.V4. C(v) je oèrtan krog pri Delaunayevi triangulaciji, ki ustreza v.
V5. V notranjosti C(v) ni nobene toèke niza P.
V6. Èe je p
j najbližji pi, potem je (pj,pi) rob triagulacije D(P).V7. Èe obstaja krog skozi toèki p
j in pi, ki ne vsebuje nobenih drugih toèk niza P, potem je (pj,pi) rob triangulacije D(P).
6.3 Konstrukcija Voronoi diagrama
6.3.1 Deterministièen algoritem za konstrukcijo Voronoi diagrama
Za konstrukcijo Voronoi diagrama obstaja cela vrsta algoritmov. Leta 1985 je Fortune [8] izdelal algoritem, ki temelji na principu pregledovanja ravnine. Na prvi pogled je nerazumljivo, kako lahko nastaja diagram za linijo, èe nanj vplivajo toèke na ravnini, ki so pred pregledovalno linijo in še niso bile pregledane.
Naj bodo toèke na xy ravnini del tridimenzionalnega koordinatnega sistema. Nad vsako toèko naj bo postavljen stožec z nagibom 45
o, ki ima vrh v toèki p. V tretji dimenziji je to mogoèe razumeti kot èas. Stožec nad toèko p predstavlja krog, ki se veèa: po èasu t ima radij t. Naj imata toèki p1 in p2 vsaka svoj stožec. Presečišèe teh dveh stožcev je krivulja v prostoru, njena projekcija pa je ravna èrta na xy ravnini (Slika 4.7).
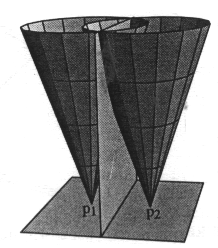
Slika 6.7 Projekcija prostorske krivulje na ravnino je daljica
Gledano iz z = - ¥ , bi projekcije vseh prostorskih krivulj, ki so preseèišèa stožcev nad toèkami p
i, predstavljale Voronoi diagram na ravnini xy. To lastnost je Fortune uporabil pri svoji metodi. Ravnina se pregleduje s pomoèjo ravnine p , ki je proti ravnini xy nagnjena za 45o. Pregledovalna èrta L je preseèišèe med ravninama p in xy. Naj bo pregledovalna èrta L vzporedna y osi, koordinata x pa naj bo l (Slika 6.8).
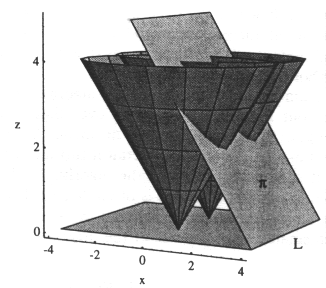
Slika 6.8
Stožca presekana s pregledovalno ravnino. Ravnina p in èrta L se pomikata v desno.
Na strani x> l èrte L je od spodaj vidna samo ravnina p
. Ta zakriva del stožcev, obenem pa predstavlja del ravnine, ki jo je potrebno še pregledati. Na strani x< l èrte L, je viden Voronoi diagram vse do preseèišèa ravnine p s stožcema. Presečišèe ravnine s stožcem je parabola in tako je tudi presečišèe ravnine p z desno stranjo stožcev parabola. Ta se na ravnino xy (gledano iz z = - ¥ ) projecira kot parabolièno èelo, ki je sestavljeno iz veèih elementarnih parabol (Slika 6.9).

Slika 6.9 Gledano iz z = - ¥ . Odebljena èrta je parabolièno èelo.
Dve paraboli se stikata v toèki, kjer se ravnina p dotika obeh stožcev. Iz prej navedenih ugotovitev je na tem mestu Voronoi rob. Ker je pregledovalna ravnina p nagnjena pod istim kotom kot stranica stožca, sreča L toèko p v trenutku, ko pregledovalna ravnina zadane ob stožec točke p. Tako Voronoi diagram ne nastaja samo levo od pregledovalne èrte L, ampak ves èas tudi pod ravnino p . Torej: Vornoi diagram nastaja levo od pregledovalne èrte L, navzgor do paraboliènega èela, ki za L nekoliko zaostaja.
6.3.2 Inkrementalni algoritem za konstrukcijo Voronoi diagrama
Inkrementalni algoritem za konstrukcijo Voronoi diagrama [7] temelji na postopnem dodajanju toèk niza P po nakljuènem vrstnem redu; podobno kot že opisani inkrementalni algoritmi. Naj bo P niz toèk na ravnini in V(P) Voronoi diagram, ki ga te toèke doloèajo. Naj bo Pi niz prvih i nakljuèno izbranih toèk. Na vsaki stopnji i algoritem doloèi Voronoi diagram V(Pi). Diagram V(Pi+1) nastane iz V(Pi) kot je prikazano na Sliki 6.10.
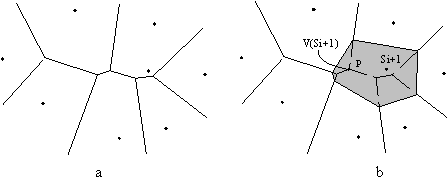
Slika 6.10 (a) V(Pi); (b) V(Pi+1); (b) obmoèje Si+1.
Naj bo S= Si+1 i+1 toèka, ki je na ravnino dodana nakljuèno. Najprej je potrebno poiskati toèko v V(Pi), ki leži v Voronoi območju toèke S. V tem primeru je S bližja točki p kot katerikoli drugi sosednji toèki v V(Pi). Jasno je, da toèka p ne bo veè del diagrama V(Pi+1) . V vsakem trenutku dodajanja i+1 je možnih več toèk p, vendar zadostuje ena sama, ki je izbrana nakljuèno. Ostale toèke (temena Voronoi diagrama), ki so v obmoèju S, je moè poiskati v diagramu V(Pi). Iskanje se zaène v toèki p in je preprosto izvedljivo, saj so sosednja temena med seboj povezana z Voronoi robovi. Robovi, ki so temenom p sosednji, se skrajšajo ali odstranijo. Èe ima Voronoi rob obe krajišèi v toèkah p, se odstrani, èe pa je toèka p samo eno krajišèe, se rob skrajša. Na koncu je potrebno doloèiti še robove Voronoi obmoèja dodane toèke S. Ti robovi povezujejo med seboj krajišèa odrezanih robov v krožnem vrstnem redu. Mesta, kjer se robovi odrežejo, so določljiva z razpolavljanjem povezav med toèko S in ostalimi sosednjimi toèkami. Tako dobljen diagram je V(Pi+1).
6.4 Aplikacije povezane z Voronoi diagrami
S konstrukcijo Voronoi diagrama je povezanih veè aplikacij: najbližji sosed, maksimiziranje najmanjših kotov pri triangulaciji, najveèji prazen krog, najmanjše razvejišèe, problem trgovskega potnika, itd.
6.4.1 Najbližji sosed
Problem najbližjega soseda je iskalne narave. Potrebno je poiskati najbližjega soseda določ
eni toèki oziroma poiskati najbližjega soseda vsaki izmed toèk niza P. S tem problemom se ukvarjajo na razliènih podroèjih: biologija, ekologija, geografija, fizika, itd.
Definicija problema:
b
je najbližji sosed a-ja, èe | a - b|
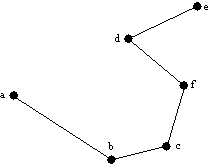
Slika 6.11 a® b, b® c ,d® e in d® f. b® a ne velja.
Naj bo P niz toèk, preko katerega se lahko doloèi Voronoi diagram. Pri iskanju najbližjega soseda toèki q se problem zreducira na iskanje Voronoi obmoèja, v katerem ta toèka leži. Vse toèke v tem obmoèju so najbližji sosedi toèki q.
6.4.2 Maksimiziranje najmanjših kotov triangulacije
Pri analiziranju kompleksnejših oblik se uporabljajo metode konènih elementov (pri naèrtovanju avtomobilskih lupin). Stabilnost numeriènega postopka je odvisna od kvalitete razdelitve. Izkaže se, da spada Delaunayeva triangulacija med dobre razdelitve. Naj bo P niz toèk, preko katerih je izvedena triangulacija. Linijski segmenti se med seboj sekajo (v svojih krajišèih) samo v toèkah niza P. Konveksna lupina je razdeljena na trikotnike. Z vidika konènih elementov je dobra tista razdelitev, ki uporablja "debele" trikotnike. Izogniti se je potrebno trikotnikom z majhnimi koti. Iz tega sledi postopek maksimiziranja najmanjših kotov. Natanèen odgovor na to je Delaunayeva triangulacija. Naj bo T triangulacija niza P, zapis kotov te triangulacije naj bo (a
1, a
2,...,a
3t), razvršèenih od najmanjšega do najveèjega, pri èemer je t število trikotnikov v T. Število T je konstantno za vsak niz P. Med dvema triangulacijama istega niza P je doloèljivo razmerje T ![]() T' glede na njuno 'debelost', èe velja: a
1>
a
1' ali a
1=
a
1' in a
2>
a
2' ali a
1=
a
1', a
2=
a
2' in a
3>
a
3' itd. Iz tega vsega sledi, da je Delaunayeva triangulacija T=D(P) najveèja glede na velikost kotov v odnosu T
T' glede na njuno 'debelost', èe velja: a
1>
a
1' ali a
1=
a
1' in a
2>
a
2' ali a
1=
a
1', a
2=
a
2' in a
3>
a
3' itd. Iz tega vsega sledi, da je Delaunayeva triangulacija T=D(P) najveèja glede na velikost kotov v odnosu T ![]() T' glede na katerokoli razdelitev T' preko niza toèk P.
T' glede na katerokoli razdelitev T' preko niza toèk P.
6.4.3 Najveèji prazen krog
Potrebno je poiskati najveèji prazen krog, èigar center je v notranjosti konveksne lupine, ki jo doloèa niz toèk S. Prazen v tem smislu, da v njegovi notranjosti ne leži nobena točka niza S in najveèji, da ne obstaja noben tak krog, ki bi imel veèji radij. V praksi je to primerljivo z iskanjem lokacije za postavitev jedrskega reaktorja, ki naj bo zgrajen èim bolj stran od naseljenih krajev. Naj bo f(p) polmer najveèjega praznega kroga s centrom v toèki p. Poiskati je potrebno maksimum te funkcije preko vseh p-jev v konveksni lupini S, H=H(S). Navidezno obstaja neskonèno možnosti za toèko ekstrema. Izkaže pa se, da jih je konèno mnogo.
Naj bo nekje v notranjosti H prazen krog s središèem v p, ki se mu lahko poveèuje polmer. V nekem trenutku bo ta krog zadel ob eno izmed toèk na ravnini S = { s1,...,sn} in imel pri tem vrednost f(p). Èe krog zadane samo ob eno toèko, npr. s1, potem je jasno, da f(p) ni najveèja možna vrednost. Èe se toèka p po premici iz p1 pomakne stran od s1 v toèko p', potem je f(p') > f(p) (Slika 6.12).
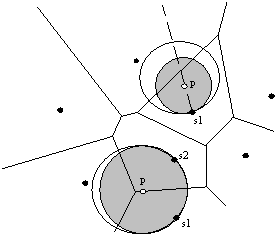
Slika 6.12 Krog skozi eno ali dve toèki na ravnini.
Recimo, da pri razdalji f(p) krog zadane ob natanèno dve toèki s1 in s2. Tudi v tem primeru f(p) ne more biti najveèja možna vrednost. Toèko p je mogoèe po razpolovnici S1S2 pomakniti stran od s1 in s2 v toèko p'. Potem velja f(p')> f(p) (Slika 6.12). Iz tega sledi, da funkcija f(p) doseže maksimum samo v primeru, če krog v enem trenutku zadane ob najmanj tri toèke hkrati. Vsako premikanje toèke p bi v tem primeru pomenilo približevanje k neki točki in s tem manjšanje f(p). Èe je torej center p najveèjega praznega kroga v notranjosti lupine H(S), potem mora p sovpadati z Voronoi temenom. Èe p leži na lupini H(S), potem mora toèka p ležati na Voronoi robu. S tem je doloèenih konèno število možnih toèk. Med vsemi je potrebno poiskati tisto, ki ima f(p)= max. Algoritem za najveèji prazen krog:
procedure RMax(p)
begin
doloèi Voronoi diagram V(S) za S;
doloèi konveksno lupino H;.
for za vsako Voronoi teme n do
begin
if vÎ H then
max f(p) s centrom v v;
end.
for za vsak Voronoi rob e do
begin
p= eÇ d H;
max f(p) s centrom v p;
end.
return f(p)max;
end.
6.4.4 Najmanjše razvejišèe
Najmanjše razvejišèe je problem, pri katerem je potrebno toèke niza S povezati med seboj tako, da bo imela nastala drevesna struktura najmanjšo mogoèo dolžino. V praksi je to primerljivo z naèrtovanjem lokalnih mrež, kjer je potrebno s kablom povezati med seboj uporabnike na razliènih lokacijah. Ideja algoritma je, da je potrebno med seboj združiti vse najkrajše robove e, ki povezujejo med seboj vse toèke niza G.
6.4.5 Problem trgovskega potnika
Problem trgovskega potnika je eden bolj prouèevanih v raèunski geometriji. Je povsem praktiène narave in ga je moè uporabiti pri številnih primerih. Glavno vprašanje je, po kateri poti naj hodi trgovski potnik, da bo obiskal vsa mesta in da bo pot najkrajša možna. Ali, kako z neprekinjeno črto povezati med seboj vse toèke niza M tako, da bo ta èrta najkrajša možna.
6.5 Posplošitve Voronoi diagrama
Lastnosti Voronoi diagrama omogoèajo posplošitve v veèih smereh, kar se izkaže kot zelo uporabno na razliènih praktiènih podroèjih. Voronoi diagram je v svoji osnovi doloèen kot niz toèk, za katere velja, da ima vsaka najmanj dve najbližji toèki iz niza toèk P. Ena izmed posplošitev je sistem srednjih osi. Srednje osi so skup toèk v notranjosti P, ki imajo najmanj dve najbližji točki na meji d P mnogokotnika P. V tem primeru prej omenjene toèke zamenja meja mnogokotnika d P. Srednje osi pravokotnika so prikazane na Sliki 6.13. Vsaka toèka horizontalnega segmenta v kvadratu je enako oddaljena od zgornjega in spodnjega roba mnogokotnika P. Vsaka toèka na diagonalnem segmentu je enako oddaljena od toèk na sosednjih robovih mnogokonika P. Bolj kompleksen primer je prikazan na Sliki 6.14. Srednje osi imajo drevesno strukturo. Vsaka toèka na srednjih oseh je središèe kroga, ki se meje mnogokonika d P dotika v najmanj dveh toèkah.
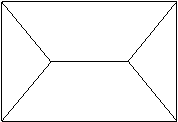
Slika 6.13 Srednje osi kvadrata
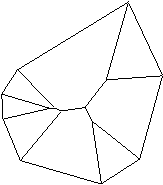
Slika 6.14 Srednje osi konveksnega mnogokotnika z n == 8 temeni
7 Zajem prostorskih toèk
Proces modeliranja v prostoru je mogoè tudi na osnovi modelov, ki so dobljeni z zajemom toèk v prostoru. Tako dobljene površine je mogoèe vkljuèiti v že obstojeèa stanja ali jih uporabiti kot osnovo za nove modele. Zajem in modifikacija obstojeèega stanja je pomemben naèin modeliranja na podroèjih, kjer so površine kompleksne in za katere popis površine ne obstaja. Vhodne koordinate toèk so lahko urejene
in popisujejo skupine površin, ali pa so neurejena množica točk, za katere površine niso opredeljene. V splošnem so površine kompleksne.Digitalizirane prostorske toèke je mogoèe z uporabo algoritmov raèunske geometrije združ
iti v mnogokotniške mreže, ki tvorijo površine. Za zahtevne površine je najbolj uporabna trikotniška mreža.
7.1 Mehanski sistem za zajemanje prostorskih toèk
Mehanski sistem je zasnovan za zajemanje prostorskih toèk. V povezavi z raèunalnikom je sposoben digitalizacije seznama urejenih ali neurejenih toèk. Sistem je sestavljen iz koordinatne mize, na katero je pritrjen mehanizem, sestavljen iz treh palic. Palica, ki je pritrjena na osnovno plošèo, je vrtljiva okoli svoje vertikalne osi, ostali dve pa sta vrtljivi okoli horizontalne osi, ki gre skozi krajišèe palice. V vsakem izmed treh vrtišè je pritrjen potenciometer, preko katerega je mogoèe doloèiti kot zasuka posamezne palice. Z upoštevanjem vseh treh relativnih kotov in dolžin palic, je mogoèe doloèiti koordinate toèke v prostoru.
Trije potenciometri so prikljuèeni vsak na svoj kanal analogno digitalnega konverterja. Ta komunicira (podatke pošilja za vsak kanal posebej) preko LPT porta z raèunalnikom s pomoèjo programa, ki upošteva karakteristike A/D konverterja. Rezultat je število med 0 in 255, s katerim je mogoèe doloèiti kot v vsakem vrtišèu in preko tega koordinate doloèene toèke v prostoru.
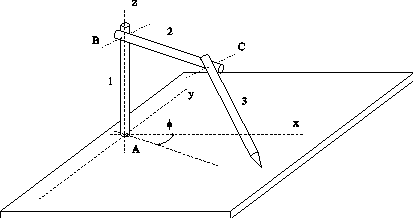
Slika 7.1 Mehanski sistem za zajemanje prostorskih toèk.
Na sliki 7.1 je prikazan mehanski sistem za zajemanje prostorskih toèk. Sestavljen je iz treh palic (1, 2 in 3) in treh potenciometrov, ki omogoèajo vrtenje v treh vrtišèih (A, B in C). Na koncu tretje palice je pritrjeno tipalo. Konico tipala je potrebno postaviti na tisto toèko v prostoru, ki s
e ji želi odčitati koordinatne vrednosti.
7.1.1 Napake pri zajemanju prostorskih toèk
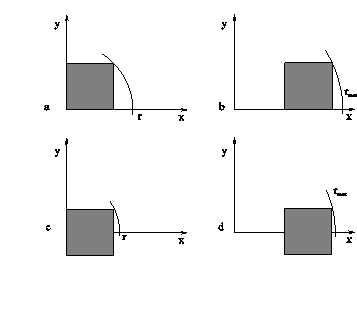
Slika 7.2
Štiri razliène postavitve modela na koordinatno mizo.
Do napak pri zajemanju prostorskih toèk pride v veèji meri zaradi zraènosti v potenciometrih in spojih, zanemarljivo majhen del pa prispeva netogost palic. Zraènost v spojih je mogoèe s primerno izvedbo zmanjšati, medtem ko se na zraènost v potenciometrih ne da vplivati. Zaradi naštetega izmerjene vrednosti odstopajo od realnih, kar vpliva na popaèenje oblike modela, ki se ga želi posneti. Na Sliki 7.2 so prikazane štiri razliène postavitve modela na koordinatno mizo in na Sliki 7.3 štiri predvidena popaèenja oblike zaradi zraènosti v vrtišèih. Senèeno podroèje predstavlja možna odstopanja oblike za kocko, ki je bila uporabljena kot model.
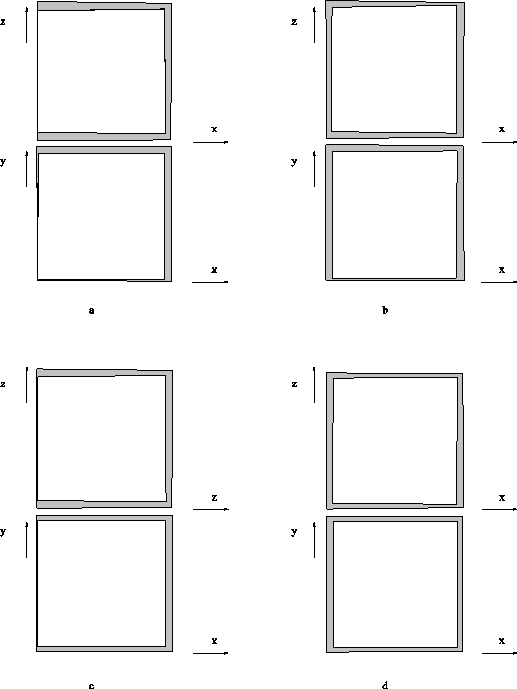
Slika 7.3 Popaèenja oblike za štiri postavitve modela iz Slike 7.2.
7.2 Napajalnik
Analogno digitalni konverter deluje pri napetosti petih voltov (Slika 7.4).
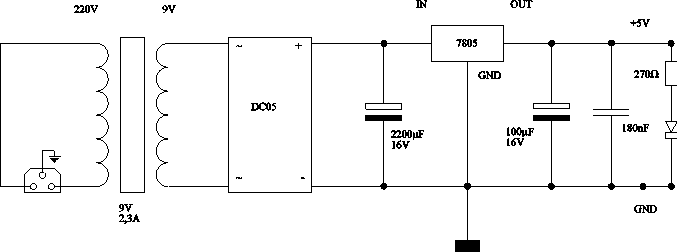
Slika 7.4 Shema napajalnika za ADC.
7.3 Analogno digitalni konverter
Za pretvarjanje podatkov iz analogne oblike v digitalno se uporablja 8-bitni analogno digitalni konverter ADC0838 [1] s serijskim I/O vh
odom in možnostjo uporabe do osmih kanalov. Pri tem se lahko uporablja vsak kanal posebej (rezultat je absolutna vrednost) ali v parih (rezultat je diferenca vrednosti na obeh kanalih).
7.3.1 Povezava A/D konverterja z raèunalnikom
A/D konverter je z raèunalnikom povezan preko kabla na LPT port. Shema povezave je prikazana na Sliki 7.5.
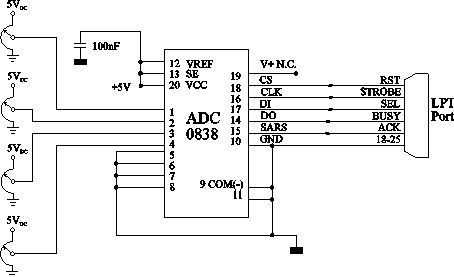
Slika 7.5 Povezava konverterja z raèunalnikom (LPT).
V tabeli 7.1 je prikazana vezava na LPT port.
Tabela 7.1: LPT port [12].
|
Pin |
Povezava |
Naslov |
Bit |
Povezava z A/D |
|
|
1 |
Not Data Strobe |
|
0x37a |
0 |
CLK |
|
10 |
Not Printer Acknowledge |
|
0x379 |
6 |
SARS |
|
11 |
Printer Busy |
BUSY |
0x379 |
7 |
DO |
|
16 |
Not Reset Printer |
|
0x37a |
2 |
|
|
17 |
Not Printer Selected |
SEL |
0x37a |
3 |
DI |
|
18-25 |
GND |
GND |
7.3.2 Komunikacija med raèunalnikom in ADC.
Delovanje AD konverterja je pod nadzorom programske opreme. Pretvorba se zaène s postavitvijo linije ![]() (chip select) na niè (Slika 7.4). Ta mora ostati na nièli ves èas pretvorbe. Tako je konverter pripravljen sprejeti prvi bit, t.j. prvi bit doloèitve kanala, s katerega naj pošlje pretvorjeno vrednost. Èas, ki ga je potrebno aktivirati na tem mestu, je doloèen s procesorjem in ga je potrebno poslati na CLK (clock) vhod konverterja.
(chip select) na niè (Slika 7.4). Ta mora ostati na nièli ves èas pretvorbe. Tako je konverter pripravljen sprejeti prvi bit, t.j. prvi bit doloèitve kanala, s katerega naj pošlje pretvorjeno vrednost. Èas, ki ga je potrebno aktivirati na tem mestu, je doloèen s procesorjem in ga je potrebno poslati na CLK (clock) vhod konverterja.
Posamezno vhodno konfiguracijo se doloèi z MUX naslavljanjem. MUX naslov doloèi, s katerega analognega kanala bo potekala pretvorba in ali bo to samostojen podatek ali pa bo v paru doloèal diferenco. MUX naslov je potrebno poslati na DI (data in) vhod A/D konverterja. V Tabeli 7.2 je prikazano MUX naslavljanje za posamezne kanale in v Tabeli 7.3 diferencialno Mux naslavljanje.
Tabela 7.2: Mux naslavljanje za posamezne kanale.
|
MUX Naslov |
Posamezen analogni kanal |
||||||||||
|
SGL/
|
ODD/ SIGN |
SELECT 1 0 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
COM |
|
1 |
0 |
0 0 |
+ |
- |
|||||||
|
1 |
0 |
0 1 |
+ |
- |
|||||||
|
1 |
0 |
1 0 |
+ |
- |
|||||||
|
1 |
0 |
1 1 |
+ |
- |
|||||||
|
1 |
1 |
0 0 |
+ |
- |
|||||||
|
1 |
1 |
0 1 |
+ |
- |
|||||||
|
1 |
1 |
1 0 |
+ |
- |
|||||||
|
1 |
1 |
1 1 |
+ |
- |
Tabela 7.3: Diferencialno Mux naslavljanje.
|
MUX Naslov |
Diferencialni analogni par |
|||||||||
|
SGL/
|
ODD/ SIGN |
SELECT 1 0 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
0 |
0 |
0 0 |
+ |
- |
||||||
|
0 |
0 |
0 1 |
+ |
- |
||||||
|
0 |
0 |
1 0 |
+ |
- |
||||||
|
0 |
0 |
1 1 |
+ |
- |
||||||
|
0 |
1 |
0 0 |
- |
+ |
||||||
|
0 |
1 |
0 1 |
- |
+ |
||||||
|
0 |
1 |
1 0 |
- |
+ |
||||||
|
0 |
1 |
1 1 |
- |
+ |
Zaèetni bit je prva logièna "1" (nièle pred tem se izpustijo), ki se pojavi na vhodu konverterja DI. Po prvem bitu konverter prièakuje še štiri bite za doloèitev MUX naslova. Ko je zaèetni bit prestavljen na zaèetno lokacijo MUX registra (t.j. za pet mest v levo), je s tem doloèen analogni kanal, s katerega bo potekala pretvorba. Na tem mestu je potreben èas 1/2 èasovne periode, da izbrani MUX kanal uskladi svoje delovanje. SAR linija se dvigne na ena, kar pomeni, da je pretvorba v teku in da vhod DI do konca pretvorbe ne sprejme nobenega signala veè. Po koncu pretvorbe se SAR linija spusti na niè. Izhodna linija DO pride iz tristanjskega položaja in v èasu usklajevalnega èasa odda zaèetno nièlo. Izhodni kanal DO zaène oddajati osem bitov, vsakega v trenutku padca linije CLK. Vsi notranji registri se izpraznijo z dvigom linije ![]() na ena.
na ena.
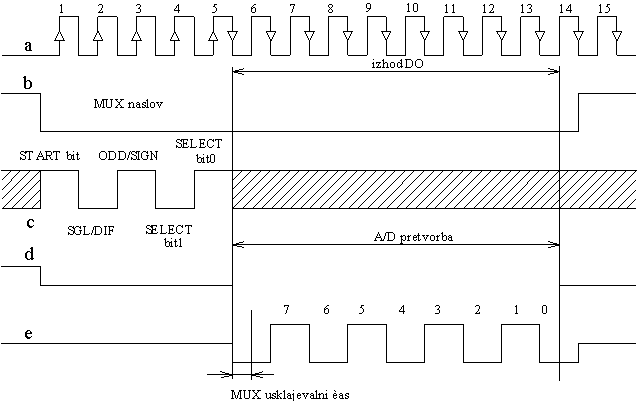
Slika 7.6 Èasovni diagram A/D pretvorbe za ADC0838 [1].
Na Sliki 7.6 je prikazan èasovni diagram poteka doloèanja analognega kanala in A/D pretvorbe. Linija a predstavlja CLK (clock), b je ![]() (chip select), c je DI (data in), d je SARS (SAR status) in e je DO (data out). Šrafirano podroèje predstavlja èas, ko DI ne sprejema nobenih signalov.
(chip select), c je DI (data in), d je SARS (SAR status) in e je DO (data out). Šrafirano podroèje predstavlja èas, ko DI ne sprejema nobenih signalov.
Algoritem doloèanja analognega kanala in branja z DO A/D pretvornika:
procedure ReadAD(channel)
begin ![]() := 0;
:= 0;
CLK := 0;
i := števec bitov;
a := naslov analognega kanala po Tabeli 7.2 - najveè pet bitov;
for i:= 0 until i< 5 do (* branje MUX naslova *)
begin if a[ peti bit] := 1 then pošlji 1 na DI else 0 na DI;
èasovna perioda;
pomik a za en bit v levo;
end. (* konec branja MUX naslova *)
a := vseh osem bitov na 0;
pavza za usklajevanje delovanja;
for i := 0 until i< 8 do (* branje z DO *)
begin èasovna perioda;
a := prebere bit z DO po Sliki 7.4 in ga vpiše v prvi bit;
pomik a za en bit v levo;
end.
![]() := 1; (* konec branja z DO *)
:= 1; (* konec branja z DO *)
end.
Funkcija je napisana v programskem jeziku C.
Na A/D konverter (![]() , CLK in DI) pošilja z naslova 0x379 in bere (DO in SARS) z naslova 0x379.
, CLK in DI) pošilja z naslova 0x379 in bere (DO in SARS) z naslova 0x379.
int iport = 0x379;
int oport = 0x37a;
Signal s
b = 0x01;
outportb( oport, b );
Èas je doloèen s spreminjanjem vrednosti na prvem bitu "0® 1® 0". Zaradi invertiranosti velja:
outportb( oport, b &= 0xFE ); /* prižge bit 0 */
outportb( oport, b ½ = 0x01 ); /* ugasne bit 0 */
Èas usklajevanja po MUX naslavljanju je doloèen z
delay(4);
in ga je potrebno prilagajati izbranemu A/D konverterju.
Z DO po vrsti prihajajo osmi, sedmi, šesti itd. biti rezulatata A/D pretvorbe na BUSY (invertiran), t.j. osmi bit. Tako je potrebno prebrano vrednost najprej prestaviti za sedem bitov v desno (t.j. v prvi bit) in pred naslednjim branjem ves zapis za en bit v levo.
a = (( ~ inportb( iport ) & 0x80 ) > > 7 ) ½ ( a< < 1);
Po konèani pretvorbi se ![]() postavi na ena:
postavi na ena:
b = 0x02;
outportb( oport, b );
7.4 Doloèanje koordinatnih vrednosti iz geometrije sistema
Koordinatne vrednosti toèk v prostoru so doloèljive v odvisnosti od geometrije sistema za zajemanje toèk v prostoru. Na Sliki 7.7 je prikazana geometrija sistema.
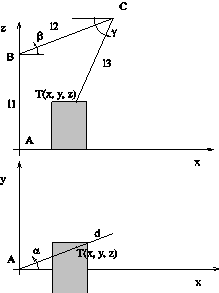
Slika 7.7 Geometrija sistema za zajemanje prostorskih toèk.
Doloèitev koordinat:
d = l
2 * cos - l3 * cos(,
koordinata x:
x = d * cos
,
koordinata y:
y = d * sin
,
koordinata z:
z = l
1 - l2 * sin - l3 * sin(.
7.5 Zapis zajetih prostorskih toèk v datoteko
Program Read.C zapisuje zajete prostorske toèke v datoteko "tocke.dat" preko funkcije ReadAD(ch), ki je predstavljena v podpoglavju 7.3.2 Komunikacija med raèunalnikom in ADC:
unsigned char ReadAD(int channel).
Program je narejen tako, da se v datoteko zapisujejo samo tiste toèke, ki se jih potrdi. Pri vsakem zapisovanju se toèke zapisujejo na konec datoteke, s èimer je omogoèeno vmesno umerjanje sistema ali zamenjava tipala zaradi nedosegljivosti posameznih delov površine.
zapis = fopen( "\\ \\ \\tocke.dat", "a" );
Funkcija ReadAD(channel) vrne vrednost med 0 in 255.
a = ( ( ~inportb( iport ) & 0x80 ) >> 7 ) | (a << 1);
return a;
Ker vsi potenciometri ne delujejo v istem obmoèju, je bilo za vsakega posebej potrebno umerjanje z linearno odsekovno interpolacijo.
A -
[ -1/6p , +1/6p ] ,B -
[ -1/12p , +1/12p ] ,C -
[ 1/12p , 1/2p ] .
a = ka * ReadAD(0) + na;
b = kb * ReadAD(1) + nb;
c = kc * ReadAD(2) + nc;
alfa = a * pi / 180;
beta = b * pi / 180;
gama = c * pi / 180;
d = l2 * cos( beta ) - l3 * cos( gama - beta );
x = d * cos( alfa );
y = d * sin( alfa );
z = l1 - l2 * sin( beta ) - l3 * sin( gama - beta);
7.6 Popaèenje oblike zaradi napake pri odèitavanju
Napake, ki nastanejo zaradi netoènosti sistema pri zajemanju posameznih toèk, se pri oblikovanju površine seštevajo tako, da je popaèenje oblike veèje, kot bi bilo mogoèe prièakovati glede na napako pri odèitavanju koordinat posamezne toèke. Na Siki 7.8 je prikazana rekonstrukcija površine plastiènega lonèka, narejena z algoritmom, opisanim v 8. poglavju. Toèke so doloèene z mehanskim sistemom za zajem prostorskih toèk.
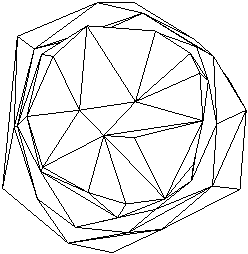
Slika 7.8 Rekonstrukcija površine plastiènega lonèka.
Na Sliki 7.9 je prikazano popaèenje oblike dna lonèka zaradi napake pri zajemanju posameznih toèk. Èrtkana èrta predstavlja dejansko obliko in velikost dna.

Slika 7.9 Dno plastiènega lonèka.
Kljub napaki, se je dejanski obliki mogoèe približati s èim veèjim številom odèitanih toèk.
8 Rekonstrukcija površin
Podan je prostorski model, ki se mu
želi digitalizirati površino. Osnovni podatek so prostorske točke
p
i = [ xi, yi, zi] Î R3, i = 1,...,n
na površini telesa, ki so bile dobljene s pomoèjo mehanskega sistema za odèitavanje 3D toèk ali na kakšen drug naèin. Na podlagi odèitanih toèk je potrebno narediti rekonstrukcijo telesa oz. rekonstrukcijo njegove površine ali samo dela njegove površine.
Naèeloma odèitane toèke niso urejene in same po sebi ne doloèajo površine, èe pa že, ta razdelitev ni nujno najboljša. Z delnim urejanjem pri odèitavanju toèk je mogoèe razširiti mož
nosti rekonstruiranja in celo izboljšati kvaliteto rekonstruirane površine. S tem je mišljena uporaba Delaunayeve triangulacije, ki je že sama po sebi najboljša, vendar je njen rezultat s primernim odčitavanjem toèk mogoèe še izboljšati. Pri urejenem odèitavanju se lahko doloèi osnovni rob telesa, ki se ga želi rekonstruirati ali pa se doloèi meja površine, ki predstavlja samo del površine celega telesa. O ostalih toèkah površine, ki jo je potrebno rekonstruirati, v veèini primerov ni nobenih podatkov. Ne o sosednosti, ne katerih koli drugih podatkov o povezanosti, naklonih in podobno.Na splošno imajo lahko odèitane toèke tudi kakšno urejenost. Lahko so urejene tako, da so za vsako ravnino posebej (y = 0, y = 1, y = 2, ...) podane vrednosti ostalih dveh koordinat in predstavljajo zaporedje ravninskih preènih prerezov.
V nadaljevajnu je predstavljena metoda, ki iz neurejenih oz. delno urejenih toèk, ki ležijo na površini telesa, omogoèa rekonstrukcijo telesa oz. dela njegove površine.
8.1 Triangulacija površine
Pri rekonstrukciji površine so uporabljeni osnovni geometrijski elementi, ki so opisani v poglavju 3. Osnovni element je toèka v prostoru
p
i = [ xi, yi, zi] Î R3, i = 1, ..., n.
Dve toèki v prostoru se lahko med seboj poveže z robom
e
i = pipj za i¹ j.
Trije robovi, ki med seboj povezujejo tri toèke prostora, doloèajo površino trikotne oblike
T
i = [ pi, pj, pk] za i ¹ j ¹ k ali Ti = [ ei, ej, ek] za i ¹ j ¹ k.
Z množico trikotnikov je mogoč
e rekonstruirati celotno ali samo delno površino modela (Slika 8.1).
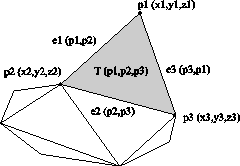
Slika 8.1 Površina sestavljena iz trikotnikov.
8.2 Delaunayeva triangulacija v 2D
V šestem poglavju je predstavljen Voronoi diagram in njegova dvojnost - Delaunayeva triangulacija. Tako Voronoi diagram kot Delaunayevo triangulacijo je mogoèe narediti tudi preko niza toèk N v prostoru. Rekonstrukcija površine, ki je opisana v nadaljevanju, je triangulacija, ki temelji na pravilih Delaunayeve triangulacije na ravnini, prenesene v prostor. Optimalni trikotniki se doloèajo s pomoèjo lokalnega postopka.
8.2.1 Najveèji prazen krog
V poglavju 6.4.3 je opisan princip najveèjega praznega kroga, ki ga je mogoèe postaviti v nek niz toèk N. Pokazano je, da center p najveèjega praznega kroga sovpada z Voronoi temenom (Slika 8.2).
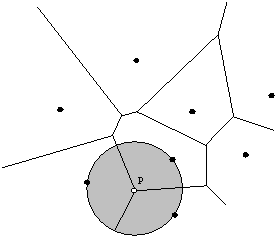
Slika 8.2 Center najveèjega praznega kroga sovpada z Voronoi temenom.
Za odnos med Voronoi diagramom in Delaunayevo triangulacio, ki se jo želi doseč
i, veljajo lastnosti, kot so opisane v podpoglavju 4.2.1.
D3. Vsak trikotnik grafa D(P) ustreza temenu grafa V(P).
Iz napisanega sledi, da postavljanje najveèjih (gledano lokalno) praznih krogov v niz toèk N hkrati pomeni tudi posredno doloèanje Delaunayeve triangulacije. Na Sliki 8.3 je prikazanih nekaj najveèjih praznih krogov in Delaunayeva triangulacija.
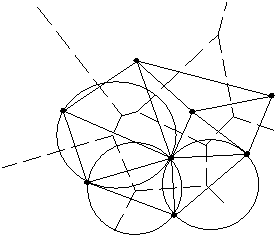
Slika 8.3 Delaunayeva triangulacija in najveèji prazen krogi.
Delaunyjev trikotnik T
i = [ pi, pj, pk] je tako mogoèe doloèiti iz nekega roba ei = pipj in tiste tretje toèke pk, skozi katero gre najveèji prazen krog, ki gre hkrati tudi skozi obe krajišèi roba pi in pj.
8.2.2 Pregledovanje ravnine
Ko so doloèene lokalne odvisnosti med posameznimi toèkami in trikotniki Delaunayeve triangulacije, je potrebno tako ureditev izpeljati èez ves niz N toèk na ravnini. V ta namen je potrebno ves niz toèk pregledati s pregledovalno èrto. Princip je podoben tistemu, ki je opisan v podpoglavju 3.5.1. Pomembna razlika je ta, da je bila pri trapezni dekompoziciji s pregledovanjem ravnine pregledovalna èrta ravna in je potovala od toèke do toèke. V primeru gradnje triangulacije je primerneje, da se pregledovalno èrto prilagodi toèkam in s tem robovom, ki jih povezujejo. Tako pregledovalna èrta ne potuje od toèke do toèke, ampak od enega pregledovalnega roba, ki je sestavljen iz veèih robov triangulacije, do naslednjega pregledovalnega roba, ki je sestavljen iz novo nastalih robov, ki so bili dobljeni z doloèanjem tretje toèke vsakega roba triangulacije posebej. Na Sliki 8.4 je prikazan niz toèk in pregledovalni rob, ki se prilagaja toèkam in že doloèenim robovom triangulacije. Pregledovalni rob potuje od leve proti desni. Štiri razliène èrte kažejo štiri razliène položaje pregledovalnega roba, ki se prilagaja obliki Delaunayeve triangulacije.
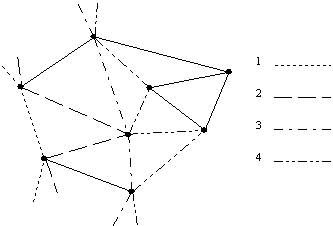
Slika 8.4
Pregledovalni rob potuje preko ravnine in se prilagaja že izgrajeni triangulaciji.
Naèeloma niti ni tako pomembno, kje se pregledovanje zaène. V tem primeru je privzet naèin iz Grahaovega algoritma, ki je opisan v podpoglavju 4.1.1.
8.2.3 Princip tretje toèke
Zaèetek pregledovanja je tako rob, ki ga doloèata najnižja, najbolj desna toèka in toèka, ki je prva najbližja po narašèujoèem kotu glede na os x (Slika 8.5).
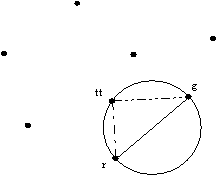
Slika 8.5 Zaèetek pregledovanja niza toèk N.
Tretja toèka je doloèljiva glede na položaj središèa oèrtanega kroga. Izmed vseh toèk, ki so levo od aktivnega roba rg, je potrebno izbrati tisto, katere odsek med središèem oèrtanega kroga in razpolovišèem aktivnega roba je najmanjši, oz. najveèji, èe je središèe oèrtanega kroga na desni strani aktivnega roba. Na Sliki 8.5 je to toèka tt. Orientiranost robov trikotnika je pomembna pri iskanju naslednjih toèk. Naslednji pregledovalni rob za Sliko 8.5 bi bil (r-tt, tt-g). Za vsak rob posebej je potrebno poiskati tretjo toèko in tako naprej, dokler ni trianguliran celoten toèk N.
8.2.3.1 Raèunanje polmera najveèjega praznega kroga
Doloèevanje tretje toèke se skrèi na doloèitev središèa oèrtanega kroga. Izraèun se poenostavi, èe se vse tri toèke prestavi v drug koordinatni sistem tako, da leži rob rg na osi x in je r(0,0).
8.3 Delaunayeva triangulacija v 3D
Izvajanje triangulacije v 3D je precej podobno opisani za 2D. Odnos med tremi toèkami v prostoru se lokalizira in prevede v problem na ravnini. Pravilnost izvajanja algoritma je mogoèe poveèati s primernim vzorèenjem. To pomeni, da morajo biti odèitane toèke posejane dovolj na gosto, še posebej, kadar je ukrivljenost ploskve velika.
8.4 Proces rekonstrukcije površine - Delaunayeva triangulacija
V nadaljevanju je predstavljen algoritem, ki je sposoben rekonstrukcije površine, ki ni nujno konveksna. Temelji na osnovnih elementih raèunske geometrije, predstavljenih v tretjem poglavju, na lastnostih Voronoi diagrama in Delaunayeve triangulacije ter kombinaciji rašitev iz posameznih algoritmov, predstavljenih v posameznih poglavjih.
8.4.1 Podatkovne strukture
Uporabljene podatkovne strukture so podobne strukturi DCEL, ki je opisana v podpoglavju 2.2.2.1, vendar so zaradi specifiènosti problema nekoliko poenostavljene. Osnovni podatek so toèke v prostoru. Vrednosti koordinat x
i, yi in zi so shranjene v polju
int T[ STT] [ 3] ,
pri èemer je STT število vseh toèk v prostoru in je postavljeno na zaèetek datoteke tocke.dat.
Pregledovalni rob, ki potuje preko površine, je doloèen s poljema
int PR[ stPR] [ 2] ,
int NPR[ stNPR] [ 2] ,
PR je aktiven pregledovalen rob, NPR je nov pregledovalen rob, ki nastaja z doloèanjem tretjih toèk posameznemu robu v PR. Pred premikom PR se NPR prepiše v PR. Pregledovalni rob so kazalci na toèke polja T.
Pri vsaki novo doloèeni tretji toèki je doloèen nov trikotnik, ki je del konène rekonstrukcije površine. Trikotniki so doloèeni v polju
int TRIK[ stTRIK] [ 3] ,
s tem, da se lahko stTRIK poljubno spreminja glede na število vseh toèk STT. TRIK so kazalci na toèke polja T; vseh je stTRIK.
Druge strukture so enake osnovnim in so uporabljene za dodatne podatke. Niz vseh robov triangulacije -
KN[ stKN] [ 2] , lupina osnovne ploskve telesa, ki leži na ravnini z = 0 - OP[ stOP] [ 2] , normale za posamezne trikotnike - NOPR[ stPR] [ 3] in NONPR[ stNPR] [ 3] ter novo nastala robova trikotnika za vsak rob PR - R1[ 2] in R2[ 2] .
8.4.2 Algoritem rekonstrukcije površine
procedure Rekonstrukcija površine(STT)
begin stNPR := 0;
stTRIK := 0;
stPR := stOP;
T [ STT] [ 3] := prebrani podatki iz datoteke tocke.dat;
PR[ stPR] [ 2] := prvi rob aktivnega regledovalnega roba;
while stPR > 0 do
begin
for iPR := 0 until iPR < stPR do
begin
ii := tretja toèka za posamezen rob PR[ iPR] [ 2] ;
if stTRIK := 0 then
begin
TRIK[ stTRIK] [ 0] := PR[ iPR] [ 0] ;
TRIK[ stTRIK] [ 1] := PR[ iPR] [ 1] ;
TRIK[ stTRIK] [ 2] := ii;
end.
else
begin
pregled, èe novo doloèeni trikotnik že obstaja
èe ne
TRIK[ stTRIK] [ 0] := PR[ iPR] [ 0] ;
TRIK[ stTRIK] [ 1] := PR[ iPR] [ 1] ;
TRIK[ stTRIK] [ 2] := ii;
end.
(* tretja toèka ii doloèi dva nova robova *)
R1[ 0] := PR[ iPR] [ 0] ;
R1[ 1] := ii;
R2[ 0] := ii;
R2[ 1] := PR[ iPR] [ 1] ;
pregled, èe novo doloèen rob R1 že obstaja v PR ali NPR
èe ne
NPR[ stNPR] [ 0] := R1[ 0] ;
NPR[ stNPR] [ 1] := R1[ 1] ;
stNPR := stNPR+1;
pregled, èe novo doloèen rob R2 že obstaja v PR ali NPR
èe ne
NPR[ stNPR] [ 0] := R2[ 0] ;
NPR[ stNPR] [ 1] := R2[ 1] ;
stNPR := stNPR+1;
end.
PR[ stPR] [ ] := NPR[ stNPR] [ ] ;
stPR := stNPR;
stNPR := 0;
end.
izpis TRIK[ stTRIK] [ ] ;
end.
8.4.3 Zaèetek pregledovanja v prostoru
Zaèetek pregledovanja toèk v prostoru je odvisen od urejenosti odèitanih toèk. Èe toèke niso urejene, je zaèetni rob lahko takšen, kot je opisano zgoraj. Druga možnost je, da se prepoznajo toèke, ki ležijo na osnovni ploskvi in doloèajo obod osnovne ploskve modela. Tako prepoznane toèke je mogoèe urediti v pregledovalni rob. Tâko pregledovanje ne izhaja iz enega samega roba, ampak iz celotnega niza. Ta naèin je primeren predvsem za simetriène oblike.
Pri branju podatkov zapiše funkcija BranjePod() vse tiste toèke, ki imajo koordinato z manjšo od dopustne napake delta, v polje OP[ stOP] .
8.4.4 Princip tretje toèke
Za vsak rob aktivnega pregledovalnega roba PR[ stPR] [ 2] je potrebno poiskati tretjo toèko, ki z njim doloèi trikotnik Delaunayeve triangulacije. Postopek poteka toliko èasa, dokler ni triangulirana celotna površina telesa. Tretja toèka se za posamezen rob doloèi z ravnino, ki se zavrti okoli aktivnega roba rg. Odnos med tremi toèkami v prostoru se prevede v ravninski problem, pri èemer gre ravnina skozi toèke r, g in tt. Na Sliki 8.6 je prikazana doloèitev tretje toèke v prostoru. Skozi toèke r, g in tt
i se postavi ravnina (t.j. prostorski odnos se prevede v ravninskega). Kot je vidno na sliki, je tretja toèka novega trikotnika toèka tt1.
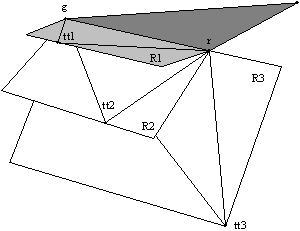
Slika 8.6 Doloèitev tretje toèke v prostoru.
Na Sliki 8.7 je prikazana triangulacija za toèke s Slike 8.6.
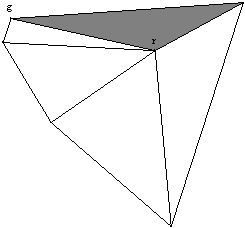
Slika 8.7 Triangulacija toèk s Slike 8.6.
8.4.4.1 Postavljanje lokalnega koordinatnega sistema
Koordinatni sistem se
iz 3D v 2D prestavi tako, da leži rob rg na os x tako, da je rx = 0 (Slika 8.8).
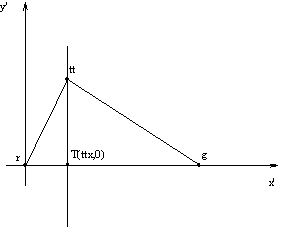
Slika 8.8 Lokalni koordinatni sistem.
Naj bodo:
p1 = [ x1, y1, z1] ,
p2 = [ x2, y2, z2] ,
p3 = [ x3, y3, z3]
toèke v prostoru, ki jih je potrebno prestaviti v ravninski koordinatni sistem. Po transformaciji so toèke:
p
1Þ r = [0,0],p
2Þ g = [gx,0],p
3Þ tt = [ttx,tty],
pri èemer velja:
gx = sqrt { (x
2-x1)2 + (y2-y1)2 + (z2-z1)2 } ,ttx = ( ![]()
tty = ½
(![]()
V novem koordinatnem sistemu je potrebno doloèiti odsek, t.j. razdaljo med središèem trikotniku oèrtanega kroga in toèko T(ttx,0). Odsek raèuna funkcija Odsek(), ki vrne +d, èe središèe trikotniku oèrtanega kroga leži levo od rg in -d, èe to leži desno od rg.
Poiskati je potrebno najmanjši pozitiven odsek ali najveèji negativen odsek. To naredi funkcija TretjaTocka().
8.4.5 Raèunanje normale
Za vsak doloèen trikotnik triangulacije se postavi normalo, ki je doloèena kot vektorski produkt dveh vektorjev. Èe je znan naklon posameznega trikotnika, se lahko doloèi kriterij, katere toèke pridejo v poštev za tretjo toèko in katere ne. To je omejitev, ki narekuje, da se pregledujejo samo toèke, ki so levo od pregledovalnega roba. Na ravnini se je predpostavka levega testirala z vektorskim produktom, v prostoru pa se testira z mešanim produktom treh vektorjev. Glede na njihovo orientiranost in predznak mešanega produkta je moè ugotoviti, na kateri strani se nahaja tretja toèka.
Normala za posamezen trikotnik je doloèena s:
for( n=0; n<3; n++ ) {
RG[n] = T[R2[1]][n] - T[R1[0]][n];
RII[n] = T[R1[1]][n] - T[R1[0]][n];
}
NONPR[stNPR][0] = RG[1]*RII[2] - RG[2]*RII[1];
NONPR[stNPR][1] = RG[2]*RII[0] - RG[0]*RII[2];
NONPR[stNPR][2] = RG[0]*RII[1] - RG[1]*RII[0];
Mešani produkt doloèa šestkratnik volumna, ki ga doloèajo trije vektorji. V odvisnosti od predznaka mešanega produkta se lahko doloèi, ali tretja toèka leži levo ali desno od pregledovalnega roba.
Mešani produkt za tri vektorje
T[g][ ]-T[r][ ], NOPR[n][ ]-T[r][ ] in T[tt][ ]-T[r][ ] je
( T[g][X]-T[r][X] ) * ( NOPR[n][Y]-T[r][Y] ) * ( T[tt][Z]-T[r][Z] )
+ ( T[g][Y]-T[r][Y] ) * ( NOPR[n][Z]-T[r][Z] ) * ( T[tt][X]-T[r][X] )
+ ( T[g][Z]-T[r][Z] ) * ( NOPR[n][X]-T[r][X] ) * ( T[tt][Y]-T[r][Y] )
- ( T[tt][X]-T[r][X] ) * ( NOPR[n][Y]-T[r][Y] ) * ( T[g][Z]-T[r][Z] )
- ( T[tt][Y]-T[r][Y] ) * ( NOPR[n][Z]-T[r][Z] ) * ( T[g][X]-T[r][X] )
- ( T[tt][Z]-T[r][Z] ) * ( NOPR[n][X]-T[r][X] ) * ( T[g][Y]-T[r][Y] );
8.5 Vhod in izhod
8.5.1 Vhod
Vhodni podatki so pridobljeni s pomoèjo mehanskega sistema za zajemanje prostorskih toèk (7.5 Zapis zajetih prostorskih toèk). Zapisane so v datoteki "tocke.dat". Prva se prebere vrednost STT, ki je število vseh toèk v prostoru, nato sledijo kordinatne vrednosti posameznih toèk. Vrednosti so med seboj loèene s presledkom. Primer datoteke "tocke.dat" za toèke v prostoru:
81
50 -20 15
45 -15 15
: : :
: : :
Vrednosti se shranijo:
STT
T[0][X] T[0][Y] T[0][Z]
T[1][X] T[1][Y] T[1][Z]
: : :
: : :
8.5.2 Izhod
Program zapiše izhodne podatke v datoteko "3DPovrs.dxf" v formatu *.dxf. S tem je omogoèeno, da se rezultat Delaunayeve triangulacije lahko pogleda in uporabiti pri modeliranju npr. v AutoCAD-u. *.dxf datoteka je standardna ASCII tekst datoteka in jo je mogoèe poljubno spreminjati za uporabo v drugih CAD okoljih [2].
Za vnos datoteke "3DPovrs.dxf" je potrebno v AutoCAD-u vpisati
Command: dxfin File name: 3DPovrs
Poleg omenjene datoteke naredi program tudi datoteko "3Dtocke.dxf", v kateri so zapisane vse prebrane toèke iz datoteke "tocke.dat" oz. polje T[STT][2].
Datoteka *.dxf je setavljena iz petih delov:
1. Header, v katerem so podani splošni podatki o risbi. Vsak parameter je sestavljen iz spremenljivke in pripadajoèe vrednosti.
2. Tables, v katerem so definirani uporabljeni koordinatni sistemi, èrte, oblike uporabljenih tekstov, pogledi, itd.
3. Blocks, v katerem so definirani bloki.
4. Entities, ki je jedro risbe. V tem delu so doloèeni vsi elementi, ki so vidni na sliki.
5. End of file.
Datoteki "3DPovrs.dxf" in "3Dtocke.dxf
" imata že vpisane prve tri dele. Program na konec dopise še četrti del in zakljuèek. Vsi parametri v datoteki *.dxf, tudi nepomembni, ki bi jih lahko izpustili, so nastavljeni nevtralno.
Oblika dela 5. Entities za izris toèke v prostoru je:
POINT
8
0
10 //x
156.0
20 //y
31.0
30 //z
0.0
Oblika dela 5. Entities za izris trikotne ploskve v prostoru je:
3DFACE
8
0
10 // prva toèka
156.0
20
31.0
30
0.0
11 // druga toèka
156.0
21
44.0
31
0.0
12 // tretja toèka
155.0
22
36.0
32
15.0
13 // èetrta toèka je pri trikotnikih enaka tretji
155.0
23
36.0
33
15.0
Oblika datoteke *.dxf [ 2] :
0 // zaèetek dela Header
SECTION
2
HEADER
// vpisani splošni podatki o risbi
0
ENDSEC // konec dela Header
0 // zaèetek dela Tables
SECTION
2
TABLES
// vpisane definicije
0
ENDSEC // konec dela Tables
0 // zaèetek dela Blocks
SECTION
2
BLOCKS
//vpisane definicije
0
ENDSEC // konec dela Blocks
0 // zaèetek dela Entities
SECTION
2
ENTITIES
// vpisani podatki
0
ENDSEC // konec dela Entities
0
EOF // konec datoteke *.dxf
8.6 Rekonstrukcija površine
Iz površine modela so prostorske toèke posnete s pomoèjo sistema za zajem prostorskih toèk in zapisane v datoteko "tocke.dat". Program naredi preko teh toèk Delaunayevo triangulacijo v prostoru, ki je najboljša možna triangulacija in je hkrati tudi rekonstrukcija površine. Rezultat se zapiše v datoteko "3DPovrs.dxf"
8.6.1 Oblika in število toèk
Kakovost rekonstrukcije površine je odvisna od števila in izbire odèitanih toèk. Na Sliki 8.9 je prikazan niz n = 57 toèk v prostoru.
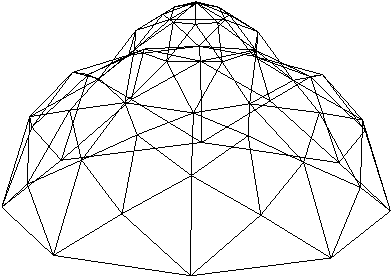
Slika 8.9 Robovi triangulacije niza N, n = 57.
Na Sliki 8.10 je prikazana rekonstrukcija površine. Vidi se, da je zaradi premajhnega števila odèitanih toèk, površina nazobèana in ne gladka, kot bi bilo prièakovati glede na model.

Slika 8.10 Rekonstrukcija površine za n = 57 prostorskih toèk.
Obliko se izboljša s poveèanjem odèitanih toèk (Sliki 8.11 in 8.12).
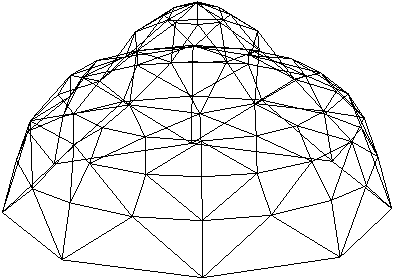
Slika 8.11 Robovi triangulacije niza N, n = 81.
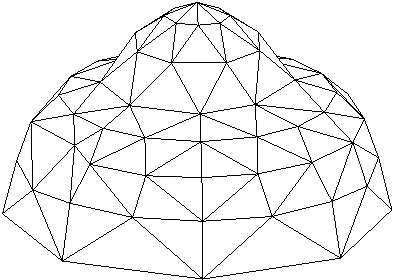

Slika 8.12 Rekonstrukcija površine za n = 51 prostorskih toèk.
Na Sliki 8.12 je vidna napaka pri odèitavanju prostorskih toèk.
8.6.2 Primer in uporaba
Na Slikah 8.13 in 8.14 je prikazana rekonstrukcija površine plastiènega lonèka. Popaèenje oblike je bilo obravnavano v poglavju 7.6. Prostorske toèke so bile odèitane s pomoèjo sistema za zajem prostorskih toèk.V prvem primeru je bil niz toèk N n = 46, v drugem pa n = 81. Vidi se vpliv števila toèk niza N na kvaliteto rekonstrukcije. Napaka pri odèitavanju je zanemarljiva, saj doseganje natanènosti sistema za zajem prostorskih toèk ni bila prioriteta naloge.
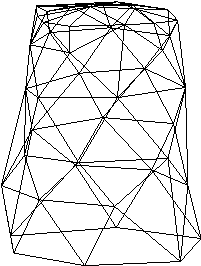
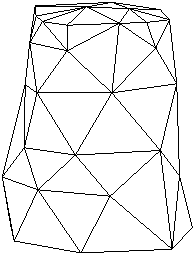
Slika 8.13 Rekonstrukcija površine plastiènega lonèka n = 46.
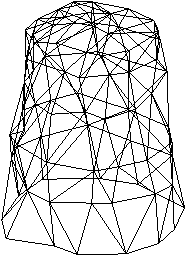
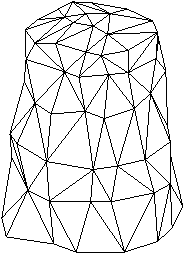
Slika 8.14 Rekonstrukcija površine plastiènega lonèka n = 81.
Na Slikah 8.15a in 8.15b je prikazana rekonstrukcija površine telefonskega aparata. Na osnovi te je mogoèe v modelirniku oblikovati konèno obliko.
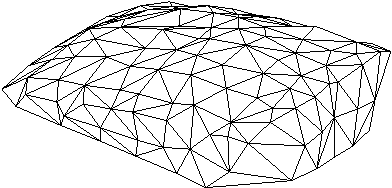
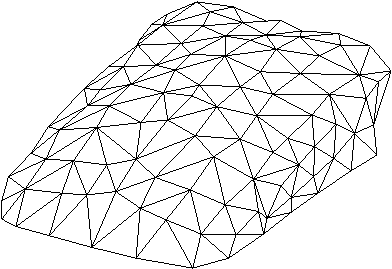
Slika 8.15 Rekonstruirana površina telefonskega aparata.
Na Slikah 8.16 in 8.17 je prikazana uporaba samo dela rekonstruirane površine. Na prvi je to del plastiènega lonèka, na drugi pa površina podstavka.
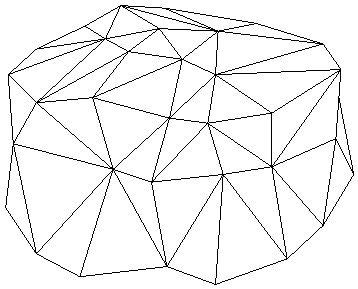
Slika 8.16 Del rekonstruirane površine plastiènega lonèka.
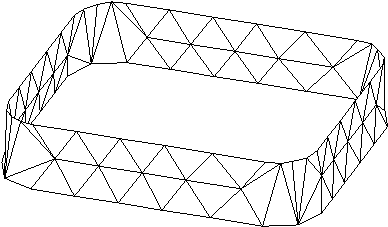
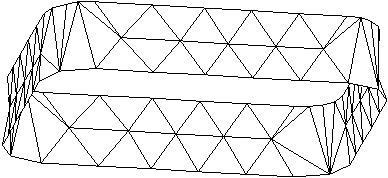
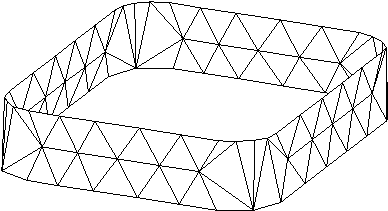
Slika 8.17 Del rekonstruirane površine podstavka.
8.7 Problemi
Pri rekonstrukciji nekonveksnih površin nastanejo problemi, ki jih pri konstrukciji konveksnih površin ni. Da
do napak ne pride, je potrebno poskrbeti že pri zajemanju prostorskih točk. Predvsem mora biti gostota toèk veèja pri veèji ukrivljenosti površine.
9 Zakljuèek
V sklopu diplomske naloge je bil izdelan mehanski sistem za zajem prostorskih toèk, ki je v povezavi z raèunalnikom sposoben digitalizacije seznama neurejenih toèk, in na osnovi algoritmov raèunske geometrije izdelan nov algoritem, ki je sposoben rekonstrukcije poljubne površine, ter program, ki zajete toèke prebere in iz njih na osnovi novega algortima generira optimalno trikotniško mrežo.
Uporabljene so osnove raèunske geometrije in deli posameznih algoritmov. Noben že napisan algoritem ni zagotavljal rekonstrukcije poljubne (ne nujno konveksne) površine, zato je bilo potrebno izdelati nov algoritem.
Za triangulacijo se uporablja Delaunayeva triangulacija, ki da optimalno trikotniško mrežo, rezultat pa je v obliki *.dxf, kar omogoč
a uvoz v prostorski modelirnik.
Izdelan je sistema za zajem prostorskih toèk in algoritem za rekonstrukcijo površine ter program za rekonstrukcijo površine, napisan v programskem jeziku C, ki je prenosljiv med razliènimi platformami.
Podrobno je predstavljen sistem za zajem prostorskih toèk in naèin digitalizacije ter povezava z raèunalnikom. Prioriteta je v prikazu funkcionalnosti in uporabnosti in ne v natanènosti sistema. Natanènost je povezana s ceno in odloèili smo se za najcenej
šo možno varianto.
Predstavljen je algoritem, ki je bil preizkušen na praktiènih primerih. Rekonstruirane površine so uporabne samostojno ali v sklopu veèje površine. V obeh primerih je površino v prostorskem modelirniku mogoèe popravljati ali prilagajati, èe v celoti ne ustreza zahtevam nadaljne uporabe.
Prostorske trikotniške mreže zaradi neprimerno odč
itanih toèk niso nujno najboljši posnetek realnega stanja. Izboljšava bi bila mogoèa s posttriangulacijskimi metodami. Tu gre predvsem za glajenje površine in optimiranje trikotniških mrež [5]. Pri glajenju gre za to, da so trikotniki postavljeni po pravilih Delaunayeve triangulacije, vendar to ni nujno posnetek dejanske oblike (Slika). Navpièni èrtkani robovi so robovi Delaunayeve triangulacije, vendar rekonstrukcija površine ni natanèen posnetek modela. Vodoravni èrtkani robovi bi bili robovi nove, zglajene površine.
Pri optimiranju trikotniške mreže pa gre za zmanjšanje števila trikotnikov na ravnejših delih površine in za poveč
anje števila trikotnikov na delih površine z veèjo ukrivljenostjo.
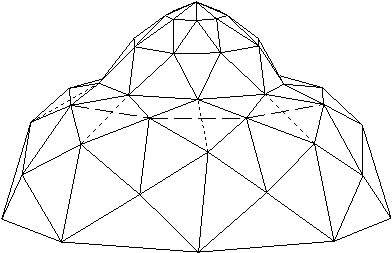
Slika
Glajenje trikotniške mreže. Črtkana èrta je rob po glajenju.
LITERATURA
[1] ADC0831/0832/0834/0838 8-Bit Serial I/O A/D Converters with Multiplexer Options, National Semiconductor Corporation, U.S.A., 1995.
[2] AutoCADâ Release 11, Reference Manual, Autodesk Ltd., England, August 1990.
[3] J. N. Bronštejn, K. A. Semendjajev, Matematièni priroènik
[4] Brian W. Kernighan, Denis M. Ritchie, Programski jezik C, Univerza Edvarda Kardelja v Ljubljani, Fakulteta za Elektrotehniko, Ljubljana, 1988.
[5] Leon Kos, Jože Duhovnik,
Physically based relaxation of unstructured meshes, DMMI 97, 3rd int. conf., str. 241 - 247.[6] Pavlina Mizori - Oblak, Matematika za študente tehnike in naravoslovja - prvi del, Univerza Edvarda Kardelja v Ljubljani, Fakulteta za Strojništvo, Ljubljana 1983. Tretja dopolnjena izdaja, 1989, str. 93 - 99.
[7] K. Mulmuley, Computational Geometry: an Introduction Through Randomized Algorithms, Prentice - Hall, Inc., 1994.
[8] Joseph O'Rourke, Computational Geometry in C, Cambridge University Press, 1993. Reprinted with corrections, 1994.
[9] È. Oblonšek, Rekonstrukcija funkcij, ploskev in teles iz razpršenih podatkov, Univerza v Mariboru, Fakulteta za elektrotehniko, raèunalništvo in informatiko, Maribor, Marec 1995.
[10] Franco P. Preparata, Michael Ian Shamos, M. I., Computation Geometry: an Introduction (Texts and monographs in computer science), Springer - Verlag, New York, 1985. Third Corrected Printing, 1990.
[11] Dave Watson, watson@maths.uwa.edu.au, Delaunay triangulation & convex hull in 2D or 3D (nnsort.c), Department of Mathematics, The University of Western Australia, Perth, December 1993.
[12] Bill Weidenauer, Amstrad personal computer PC 1640, Tehnical Reference Manual, Amstrad, 1987.
Dodatek
V dodatku so prikazani pomembnejši deli programske kode. Najprej del, ki omogoèa komunikacijo raèunalnika z AD konverterjem in zapis koordinat v datoteko tocke.dat in na koncu še del, ki naredi rekonstrukcijo površine in rezultat vpiše v datoteko 3Dpovrs.dxf.
Funkcija omogoèa komuniciranje z AD konverterjem.
unsigned char ReadAD(int channel)
{
int iport = 0x379;
int oport = 0x37a;
int i;
unsigned char a, b;
char value;
channel = (channel >> 1) | (channel << 2);
outportb( oport, 0x05 );
a = 0x18 | ( unsigned char ) channel; /* doloèi kanal */
b = 0x01; /* clk in cs na niè */
outportb( oport, b );
for( i=0; i<5; i++ ) {
if( a & 0x10 )
outportb( oport, b &= 0xF7 );
else
outportb( oport, b |= 0x08 );
outportb( oport, b &= 0xFE ); /* ugasne bit 0 */
outportb( oport, b |= 0x01 ); /* prižge bit 0 */
a = a << 1;
}
a = 0x0;
delay(4);
for( i=0; i<8; i++ ) {
outportb( oport, b &= 0xFE ); /* ugasne bit 0 */
outportb( oport, b |= 0x01 ); /* prižge bit 0 */
a = ( ( ~inportb( iport ) & 0x80 ) >> 7 ) | (a << 1);
}
b = 0x02; /* cs na ena */
outportb( oport, b );
return a;
}
Datoteka, v katero se zapisujejo z mehanskim sistemom odèitane toèke.
FILE *zapis;
zapis = fopen( "\\ \\ \\tocke.dat", "w" );
Vpisane dolžine posameznih palic mehanskega sistema.
l1 = 198;
l2 = 200;
l3 = 197;
Odsekovno linearna interpolacija za kot alfa. Podobno je tudi za ostala dva kota.
if( ( ReadAD(0) >= (A-44) ) && ( ReadAD(0) < (A-29) ) ) {
ka = -1;
na = 45+A-44; }
else if( ( ReadAD(0) >= (A-29) ) && ( ReadAD(0) < (A-15) ) ) {
ka = -1.071428571;
na = 30-ka*(A-29); }
else if( ( ReadAD(0) >= (A-15) ) && ( ReadAD(0) < (A+15) ) ) {
ka = -1;
na = A; }
else if( ( ReadAD(0) >= (A+15) ) && ( ReadAD(0) < (A+29) ) ) {
ka = -1.071428571;
na = -15-ka*(A+15); }
else if( ( ReadAD(0) >= (A+29) ) && ( ReadAD(0) <= (A+44) ) ) {
ka = -1;
na = -30+A+29; }
Doloèanje kota v stopinjah.
a = ka * ReadAD(0) + na;
b = kb * ReadAD(1) + nb;
c = kc * ReadAD(2) + nc;
Doloèitev koordinat toèke v prostoru.
d = l2 * cos( beta ) - l3 * cos( gama - beta );
x = d * cos( alfa );
y = d * sin( alfa );
z = l1 - l2 * sin( beta ) - l3 * sin( gama - beta);
Zapis koordinat v datoteko.
fprintf( zapis, "\n%d\t%d\t%d", x, y, z );
BranjePod prebere podatke iz datoteke tocke.dat. Toèke, pri katerih je koordinatna vrednost manjša od dopustne napake delta, popravi in vpiše v OP[stOP]. S pomoèjo tega polja se doloèi zaèetek pregledovanja.
void BranjePod( void ) {
FILE *podatki;
int i;
podatki = fopen( "\\ \\ \\tocke.dat", "rt" );
fscanf( podatki, "%i", &STT );
T = ( int** ) malloc( sizeof( int* ) *STT );
for( i=0; i<STT; i++ )
T[i] = (int*) malloc( sizeof( int ) *DIM );
for( i=0; i<STT; i++ ) {
fscanf( podatki, "%i%i%i", &T[i][X], &T[i][Y], &T[i][Z] );
if( T[i][Z] < delta ) {
T[i][Z] = 0;
OP[stOP] = i;
stOP++;
}
}
fclose(podatki);
}
Zapiše trikotnike mreženja v datoteko 3Dpovrs.dxf. Ta oblika zagotavlja uvoz v prostorski modelirnik. Podobna je funkcija, ki zapisuje vse odč
itane toèke v 3Dtocke.dxf.
int PisanjE( stTRIK ) {
FILE *dxf;
int i;
/* prvi del datoteke je že narejen */
dxf = fopen( "\\ \\ \\3dpovrs1.dxf", "a" );
fprintf( dxf, "ENTITIES" );
/* zapiše trikotnie v datoteko *.dxf */
for( i=0; i<stTRIK; i++ ) {
fprintf( dxf, "\n 0\n3DFACE\n 8\n0" );
fprintf( dxf, "\n 10\n%d.0\n 20\n%d.0\n 30\n%d.0", T[TRIK[i][0]][0], T[TRIK[i][0]][1], T[TRIK[i][0]][2] );
fprintf( dxf, "\n 11\n%d.0\n 21\n%d.0\n 31\n%d.0", T[TRIK[i][1]][0], T[TRIK[i][1]][1], T[TRIK[i][1]][2] );
fprintf( dxf, "\n 12\n%d.0\n 22\n%d.0\n 32\n%d.0", T[TRIK[i][2]][0], T[TRIK[i][2]][1], T[TRIK[i][2]][2] );
fprintf( dxf, "\n 13\n%d.0\n 23\n%d.0\n 33\n%d.0", T[TRIK[i][2]][0], T[TRIK[i][2]][1], T[TRIK[i][2]][2] );
}
/* napiše konec *.dxf datoteke */
fprintf( dxf, "\n 0\nENDSEC\n 0\nEOF" );
}
Naslednja funkcija raèuna dvojno površino trikotnika. To je uporabljeno pri doloèevanju lege središèa trikotniku oèrtanega kroga.
float Povrsina2( float rx, float ry, float gx, float gy, float ttx, float tty ) {
return
( rx * gy ) - ( ry * gx ) +
( ry * ttx ) - ( rx * tty ) +
( gx * tty ) - ( ttx * gy );
}
Volumen6 raèuna šestkratni volumen med štirimi toèkami. Za doloèanje položaja toèke glede na ravnino.
float Volumen6( int r, int g, int n, int tt ) {
return
( T[g][X]-T[r][X] ) * ( NOPR[n][Y]-T[r][Y] ) * ( T[tt][Z]-T[r][Z] )
+ ( T[g][Y]-T[r][Y] ) * ( NOPR[n][Z]-T[r][Z] ) * ( T[tt][X]-T[r][X] )
+ ( T[g][Z]-T[r][Z] ) * ( NOPR[n][X]-T[r][X] ) * ( T[tt][Y]-T[r][Y] )
- ( T[tt][X]-T[r][X] ) * ( NOPR[n][Y]-T[r][Y] ) * ( T[g][Z]-T[r][Z] )
- ( T[tt][Y]-T[r][Y] ) * ( NOPR[n][Z]-T[r][Z] ) * ( T[g][X]-T[r][X] )
- ( T[tt][Z]-T[r][Z] ) * ( NOPR[n][X]-T[r][X] ) * ( T[g][Y]-T[r][Y] );
}
Naslednja funkcija doloèi najnižjo toèko, t.j. prvo toèko prvega pregledovalnega roba.
int NajnizTocka( void ) {
int i; /*indeks toèke*/
int m = 0; /*indeks najnižje toč
ke doslej*/
for ( i = 1; i < stOP; i++) {
if ( (T[OP[i]][Y] < T[OP[m]][Y]) ||
((T[OP[i]][Y] == T[OP[m]][Y]) &&
(T[OP[i]][X] > T[OP[m]][X]))
)
m = i;
}
return OP[m];
}
Odsek izraèuna odsek za pregledovalni rob in tretjo toèko. Glede na velikost in predznak odseka se doloèi tretja toèka.
float Odsek( int r, int g, int tt ) {
int a, i;
float pov2, sx, sy, d2, rx, ry, gx, gy, ttx, tty, tx2, ty2, kkt2, n2;
/* za transformacijo */
float Tn[3][2]; /* nov koord. sist. */
float t12[3], t13[3]; /* vektorja 12 in 13 */
float abs_t12; /* abs vrednost 12 */
float e12[3]; /* enotski vektor 12 */
float p, d, di, dj, dk;
for( i=0; i<=2; i++ ) {
t12[i] = T[g][i] - T[r][i]; /* doloci vektor 12 */
}
abs_t12 = sqrt( t12[0]*t12[0] + t12[1]*t12[1] + t12[2]*t12[2] );
for( i=0; i<=2; i++)
e12[i] = t12[i] / abs_t12;
/* p je projekcija */
p = ( ( t13[0]*t12[0] + t13[1]*t12[1] + t13[2]*t12[2] ) / abs_t12 );
/* t31 x e12 */
di = t13[1]*e12[2] - t13[2]*e12[1];
dj = t13[2]*e12[0] - t13[0]*e12[2];
dk = t13[0]*e12[1] - t13[1]*e12[0];
/* d je razdalja od premice do toèke */
d = sqrt( di*di + dj*dj + dk*dk );
/* toèke v novem koordinatnem sistemu */
sx = 0;
sy = 0;
rx = 0;
ry = 0;
gx = abs_t12;
gy = 0;
ttx = p;
tty = d;
a = 2;
if( ( rx == ttx ) || ( gx == ttx ) ) a = 1;
switch( a ) {
case 1:
d2 = ( tty * tty ) / 4;
sx = gx / 2;
sy = tty / 2;
break;
case 2:
tx2 = ttx / 2;
ty2 = tty / 2;
kkt2 = -( tx2 / ty2 );
n2 = ty2 - kkt2 * tx2;
sx = gx / 2;
sy = kkt2 * sx + n2;
d2 = sy * sy;
break;
}
pov2 = Povrsina2( rx, ry, gx, gy, sx, sy );
/* poz d2, èe lezi (sx,sy) levo oz. neg d2, èe lezi (sx, sy) desno */
if( pov2 < 0 ) return -(d2);
else return d2;
}
Funkcija vrne indeks tretje toèke.
int TretjaTocka( int r, int g, int iPR ) {
int i;
int iNeg, iPoz;
float dPozMin, dNegMax;
float Ods, Vol;
dPozMin = 20000;
dNegMax = 0;
iNeg = 9999;
iPoz = 9999;
/* zanka preko vseh toèk na ravnini */
for( i=0; i<STT; i++ ) {
if( (i==r) || (i==g) ) goto Naslednja;
if( (l == 1) &&
(Povrsina2( T[r][X], T[r][Y], T[g][X], T[g][Y], T[i][X], T[i][Y] ) == 0 )
) goto Naslednja;
if ( l == 1 ) goto PrviRob;
Vol = Volumen6( r, g, iPR, i );
if( Vol >= 0 ) goto Naslednja; /* toèka je pred ravnino mora biti zadaj */
PrviRob:;
Ods = Odsek( r, g, i );
/* èe je središèe kroga levo - i za sx in sy */
if ( ( Ods >= 0 ) && ( Ods < dPozMin ) ) {
dPozMin = Ods;
iPoz = i;
}
/* èe je središèe kroga desno - i za sx in sy */
if( ( Ods < 0 ) && ( Ods < dNegMax ) ) {
dNegMax = Ods;
iNeg = i;
}
Naslednja:;
if( iNeg != 9999 ) return iNeg;
else return iPoz;
}
Preveri, èe so novonastali robovi pregledovalnega roba že bili upoštevani. Podoben naèin je pri preverjanju tikotnikov.
int Pregled( int R[2], int Niz[stt][2], int stEl ) {
int i;
if( stEl == 0 ) return 1;
for( i=0; i<stEl; i++ ) {
if( ( R[0] == Niz[i][0] ) && ( R[1] == Niz[i][1] ) ||
( R[1] == Niz[i][0] ) && ( R[0] == Niz[i][1] ) )
return 0;
}
return 1;
}
Zaèetne vrednosti števcev:
stPR = 1;
stNPR = 0;
stKN = 0;
stTRIK = 0;
BranjePod();
Doloèi se prvi pregledovalni rob.
PR[0][0] = NajnizTocka();
PR[0][1] = DrugaTocka();
Pregledovanje poteka, dokler je v PR še kakšen aktiven pregledovalni rob.
while( stPR>0 ) {
for( iPR=0; iPR<stPR; iPR++ ) {
Doloèi se tretja toèka posameznem robu.
ii = TretjaTocka( PR[iPR][0], PR[iPR][1], iPR );
if( ii == 9999 ) goto NaslednjiRob;
Pregleda trikotnike. Èe novo doloèen trikotnik še ne obstaja, se ga vpiše v niz.
if( PregleD( stTRIK, PR[iPR][0], PR[iPR][1], ii ) ) {
TRIK[stTRIK][0] = PR[iPR][0];
TRIK[stTRIK][1] = PR[iPR][1];
TRIK[stTRIK][2] = ii;
stTRIK++;
Pregleda vsak novo nastali rob in doloèi normalo trikotnika.
if( ( Pregled( R1, KN, stKN ) ) &&
( Pregled( R1, PR, stPR ) ) &&
( Pregled( R1, NPR, stNPR ) ) ) {
for( n=0; n<3; n++ ) {
RG[n] = T[R2[1]][n] - T[R1[0]][n];
RII[n] = T[R1[1]][n] - T[R1[0]][n];
}
NONPR[stNPR][0] = RG[1]*RII[2] - RG[2]*RII[1];
NONPR[stNPR][1] = RG[2]*RII[0] - RG[0]*RII[2];
NONPR[stNPR][2] = RG[0]*RII[1] - RG[1]*RII[0];
Vpisuje v novo nastali pregledovalni rob.
NPR[stNPR][0] = R1[0];
NPR[stNPR][1] = R1[1];
stNPR++;
Prepiše robove in trikotnikom pripadajoèe normale iz NPR v PR
for( iNPR=0; iNPR<stNPR; iNPR++ ) {
PR[iNPR][0] = NPR[iNPR][0];
PR[iNPR][1] = NPR[iNPR][1];
NOPR[iNPR][0] = NONPR[iNPR][0];
NOPR[iNPR][1] = NONPR[iNPR][1];
NOPR[iNPR][2] = NONPR[iNPR][2];
stPR = stNPR;
stNPR = 0;
Zapiše vhodne in izhodne poratke v datoteko *.dxf
PisanjE( stTRIK );
PisanjET( STT );
IZJAVA
Diplomsko delo sem samostojno izdelal pod vodstvom mentorja izr. prof. dr. Jožeta Duhovnika, dipl. ing.
Aleš DROLC
Ljubljana, dne 11.9.1997